Запрос «sin» перенаправляется сюда; см. также другие значения.
Запрос «sec» перенаправляется сюда; см. также другие значения.
Запрос «Синус» перенаправляется сюда; см. также другие значения.
Рис. 1
Графики тригонометрических функций: синуса косинуса тангенса котангенса секанса косеканса
Тригонометри́ческие фу́нкции — элементарные функции, которые исторически возникли при рассмотрении прямоугольных треугольников и выражали зависимости сторон этих треугольников от острых углов при гипотенузе (или, что эквивалентно, зависимость хорд и высот от центрального угла в круге). Эти функции нашли широчайшее применение в самых разных областях науки. Впоследствии определение тригонометрических функций было расширено, их аргументом теперь может быть произвольное вещественное или даже комплексное число. Наука, изучающая свойства тригонометрических функций, называется тригонометрией.
К тригонометрическим функциям относятся:
- прямые тригонометрические функции
- синус (sin x)
- косинус (cos x)
- производные тригонометрические функции
- тангенс (tg x)
- котангенс (ctg x)
- другие тригонометрические функции
- секанс (sec x)
- косеканс (cosec x)
В западной литературе тангенс, котангенс и косеканс обозначаются tan x, cot x, csc x.
Кроме этих шести, существуют также некоторые редко используемые тригонометрические функции (версинус и т.д.), а также обратные тригонометрические функции (арксинус, арккосинус и т. д.), рассматриваемые в отдельных статьях.
Синус и косинус вещественного аргумента являются периодическими непрерывными и неограниченно дифференцируемыми вещественнозначными функциями. Остальные четыре функции на вещественной оси также вещественнозначные, периодические и неограниченно дифференцируемые на области определения, но не непрерывные. Тангенс и секанс имеют разрывы второго рода в точках ±πn + π/2, а котангенс и косеканс — в точках ±πn.
Содержание
- 1 Способы определения
- 1.1 Геометрическое определение
- 1.1.1 Определение тригонометрических функций для острых углов
- 1.2 Определение тригонометрических функций как решений дифференциальных уравнений
- 1.3 Определение тригонометрических функций как решений функциональных уравнений
- 1.4 Определение тригонометрических функций через ряды
- 1.1 Геометрическое определение
- 2 Значения тригонометрических функций для некоторых углов
- 2.1 Значения тригонометрических функций нестандартных углов
- 3 Свойства тригонометрических функций
- 3.1 Простейшие тождества
- 3.2 Непрерывность
- 3.3 Чётность
- 3.4 Периодичность
- 3.5 Формулы приведения
- 3.6 Формулы сложения
- 3.7 Формулы для кратных углов
- 3.8 Произведения
- 3.9 Степени
- 3.10 Суммы
- 3.11 Однопараметрическое представление
- 4 Производные и интегралы
- 5 Тригонометрические функции комплексного аргумента
- 5.1 Определение
- 5.2 Комплексные графики
- 6 История названий
- 7 См. также
- 8 Литература
- 9 Ссылки
Способы определения
Геометрическое определение
Рис. 2
Определение тригонометрических функций
Обычно тригонометрические функции определяются геометрически. Пусть нам дана декартова система координат на плоскости, и построена окружность радиуса R с центром в начале координат O. Измерим углы как повороты от положительного направления оси абсцисс до луча OB. Направление против часовой стрелки считается положительным, по часовой стрелке отрицательным. Абсциссу точки В обозначим xB, ординату обозначим yB (см. рисунок).
Рис. 3
Численные значения тригонометрических функций угла 
Ясно, что значения тригонометрических функций не зависят от величины радиуса окружности R в силу свойств подобных фигур. Часто этот радиус принимают равным величине единичного отрезка, тогда синус равен просто ординате yB, а косинус — абсциссе xB. На рисунке 3 показаны величины тригонометрических функций для единичной окружности.
Если α — вещественное число, то синусом α в математическом анализе называется синус угла, радианная мера которого равна α, аналогично для прочих тригонометрических функций.
Определение тригонометрических функций для острых углов
Рис. 4
Тригонометрические функции острого угла
Во многих учебниках элементарной геометрии до настоящего времени тригонометрические функции острого угла определяются как отношения сторон прямоугольного треугольника. Пусть OAB — треугольник с углом α. Тогда:
- Синусом угла α называется отношение AB/OB (отношение противолежащего катета к гипотенузе).
- Косинусом угла α называется отношение ОА/OB (отношение прилежащего катета к гипотенузе).
- Тангенсом угла α называется отношение AB/OA (отношение противолежащего катета к прилежащему).
- Котангенсом угла α называется отношение ОА/AB (отношение прилежащего катета к противолежащему).
- Секансом угла α называется отношение ОB/OA (отношение гипотенузы к прилежащему катету).
- Косекансом угла α называется отношение ОB/AB (отношение гипотенузы к противолежащему катету).
Построив систему координат с началом в точке O, направлением оси абсцисс вдоль OA и в случае необходимости изменив ориентацию (перевернув) треугольник так, чтобы он находился в первой четверти системы координат, и затем, построив окружность с радиусом, равным гипотенузе, сразу находим, что такое определение функций приводит к тому же результату, что и предыдущее.
Данное определение имеет некоторое педагогическое преимущество, так как не требует введения понятия системы координат, но также и такой крупный недостаток, что невозможно определить тригонометрические функции даже для тупых углов, которые необходимо знать при решении элементарных задач про тупоугольные треугольники (см.: Теорема синусов, Теорема косинусов).
Определение тригонометрических функций как решений дифференциальных уравнений
Функции косинус и синус можно определить как чётное (косинус) и нечётное (синус) решение дифференциального уравнения
с начальными условиями 
Определение тригонометрических функций как решений функциональных уравнений
Функции косинус и синус можно определить как непрерывные решения (f и g соответственно) системы функциональных уравнений:
Определение тригонометрических функций через ряды
Используя геометрию и свойства пределов, можно доказать, что производная синуса равна косинусу и что производная косинуса равна минус синусу. Тогда можно воспользоваться теорией рядов Тейлора и представить синус и косинус в виде степенны́х рядов:
Пользуясь этими формулами, а также уравнениями 



где
— числа Бернулли,
— числа Эйлера.
Значения тригонометрических функций для некоторых углов
Значения синуса, косинуса, тангенса, котангенса, секанса и косеканса для некоторых углов приведены в таблице. («∞» означает, что функция в указанной точке не определена, а в её окрестности стремится к бесконечности).
 |
0°(0 рад) | 30° (π/6) | 45° (π/4) | 60° (π/3) | 90° (π/2) | 180° (π) | 270° (3π/2) | 360° (2π) |
|---|---|---|---|---|---|---|---|---|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Значения косинуса и синуса на окружности.
Значения тригонометрических функций нестандартных углов
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Значения тригонометрических функций прочих углов
Свойства тригонометрических функций
Простейшие тождества
Поскольку синус и косинус являются соответственно ординатой и абсциссой точки, соответствующей на единичной окружности углу α, то, согласно уравнению единичной окружности или теореме Пифагора, имеем:
Это соотношение называется основным тригонометрическим тождеством.
Деля это уравнение на квадрат косинуса и синуса соответственно имеем далее:
Непрерывность
Синус и косинус — непрерывные функции. Тангенс и секанс имеют точки разрыва 
Чётность
Косинус и секанс — чётные. Остальные четыре функции — нечётные, то есть:
Периодичность
Функции 


Формулы приведения
Формулами приведения называются формулы следующего вида:
Здесь f — любая тригонометрическая функция, g — соответствующая ей кофункция (то есть косинус для синуса, синус для косинуса, тангенс для котангенса, котангенс для тангенса, секанс для косеканса и косеканс для секанса), n — целое число. Перед полученной функцией ставится тот знак, который имеет исходная функция в заданной координатной четверти при условии, что угол α острый, например:
Некоторые формулы приведения:
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Формулы сложения
Значения тригонометрических функций суммы и разности двух углов:
Аналогичные формулы для суммы трёх углов:
Формулы для кратных углов
Формулы двойного угла:
Формулы тройного угла:
Прочие формулы для кратных углов:
следует из формулы дополнения и формулы Гаусса для Гамма-функции
Формулы половинного угла:
Произведения
Формулы для произведений функций двух углов:
Аналогичные формулы для произведений синусов и косинусов трёх углов:
Формулы для произведений тангенсов и котангенсов трёх углов можно получить, поделив правые и левые части соответствующих равенств, представленных выше.
Степени
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Суммы
Для функций от аргумента 
где угол 
Однопараметрическое представление
Все тригонометрические функции можно выразить через тангенс половинного угла.
Производные и интегралы
Все тригонометрические функции непрерывно и неограниченно дифференцируемы на всей области определения:
Интегралы тригонометрических функций на области определения выражаются через элементарные функции следующим образом:
Тригонометрические функции комплексного аргумента
Определение
Формула Эйлера:
позволяет определить тригонометрические функции от комплексных аргументов через экспоненту или (с помощью рядов) как аналитическое продолжение их вещественных аналогов:
где
Соответственно, для вещественного x,
Комплексные синус и косинус тесно связаны с гиперболическими функциями:
Большинство перечисленных выше свойств тригонометрических функций сохраняются и в комплексном случае. Некоторые дополнительные свойства:
- комплексные синус и косинус, в отличие от вещественных, могут принимать сколь угодно большие по модулю значения;
- все нули комплексных синуса и косинуса лежат на вещественной оси.
Комплексные графики
На следующих графиках изображена комплексная плоскость, а значения функций выделены цветом. Яркость отражает абсолютное значение (чёрный — ноль). Цвет изменяется от аргумента и угла согласно карте.
|
|
|
|
|
|
|
 |
 |
 |
 |
 |
 |
История названий
Линия синуса у индийских математиков первоначально называлась «арха-джива» («полутетива», то есть половина хорды), затем слово «арха» было отброшено и линию синуса стали называть просто «джива». Арабские переводчики не перевели слово «джива» арабским словом «ватар», обозначающим тетиву и хорду, а транскрибировали арабскими буквами и стали называть линию синуса «джиба». Так как в арабском языке краткие гласные не обозначаются, а долгое «и» в слове «джиба» обозначается так же, как полугласная «й», арабы стали произносить название линии синуса «джайб», что буквально обозначает «впадина», «пазуха». При переводе арабских сочинений на латынь европейские переводчики перевели слово «джайб» латинским словом sinus, имеющим то же значение.
Современные краткие обозначения sin и cos введены Уильямом Отредом и закреплены в трудах Эйлера.
Термины «тангенс» (от лат. tangens — касающийся) и «секанс» (лат. secans — секущий) были введены датским математиком Томасом Финке (1561—1656) в его книге «Геометрия круглого» (Geometria rotundi, 1583).
Сам термин тригонометрические функции введён Клюгелем в 1770 году.
См. также
- Гиперболические функции
- Интегральный синус
- Интегральный косинус
- Обратные тригонометрические функции
- Решение треугольников
- Синус-верзус
- Сферическая тригонометрия
- Функция Гудермана
- Четырёхзначные математические таблицы (Таблицы Брадиса)
- Эллиптические функции
Литература
- Бронштейн И. Н., Семендяев К. А. Прямолинейная тригонометрия // Справочник по математике. — Изд. 7-е, стереотипное. — М.: Государственное издательство технико-теоретической литературы, 1967. — С. 179—184.
- Г. Б. Двайт Тригонометрические функции // Таблицы интегралов и другие математические формулы. — 4-е изд. — М.: Наука, 1973. — С. 70—102.
Ссылки
- GonioLab — прояснённая единичная окружность, тригонометрические и гиперболические функции (Java Web Start)
- Weisstein, Eric W. Тригонометрические функции (англ.) на сайте Wolfram MathWorld.
- Онлайн калькулятор: вычисление значений тригонометрических функций
- Интерактивная карта значений тригонометрических функций
| Sine and cosine | |
|---|---|
 |
|
| General information | |
| General definition | ![{displaystyle {begin{aligned}&sin(alpha )={frac {textrm {opposite}}{textrm {hypotenuse}}}\[8pt]&cos(alpha )={frac {textrm {adjacent}}{textrm {hypotenuse}}}\[8pt]end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ea2762f231f5fdc1dcfacd59c303106f596ab2e1) |
| Fields of application | Trigonometry, Fourier series, etc. |
In mathematics, sine and cosine are trigonometric functions of an angle. The sine and cosine of an acute angle are defined in the context of a right triangle: for the specified angle, its sine is the ratio of the length of the side that is opposite that angle to the length of the longest side of the triangle (the hypotenuse), and the cosine is the ratio of the length of the adjacent leg to that of the hypotenuse. For an angle 


More generally, the definitions of sine and cosine can be extended to any real value in terms of the lengths of certain line segments in a unit circle. More modern definitions express the sine and cosine as infinite series, or as the solutions of certain differential equations, allowing their extension to arbitrary positive and negative values and even to complex numbers.
The sine and cosine functions are commonly used to model periodic phenomena such as sound and light waves, the position and velocity of harmonic oscillators, sunlight intensity and day length, and average temperature variations throughout the year. They can be traced to the jyā and koṭi-jyā functions used in Indian astronomy during the Gupta period.
Notation[edit]
Sine and cosine are written using functional notation with the abbreviations sin and cos.
Often, if the argument is simple enough, the function value will be written without parentheses, as sin θ rather than as sin(θ).
Each of sine and cosine is a function of an angle, which is usually expressed in terms of radians or degrees. Except where explicitly stated otherwise, this article assumes that the angle is measured in radians.
Definitions[edit]
Right-angled triangle definitions[edit]
For the angle α, the sine function gives the ratio of the length of the opposite side to the length of the hypotenuse.
To define the sine and cosine of an acute angle α, start with a right triangle that contains an angle of measure α; in the accompanying figure, angle α in triangle ABC is the angle of interest. The three sides of the triangle are named as follows:
- The opposite side is the side opposite to the angle of interest, in this case side a.
- The hypotenuse is the side opposite the right angle, in this case side h. The hypotenuse is always the longest side of a right-angled triangle.
- The adjacent side is the remaining side, in this case side b. It forms a side of (and is adjacent to) both the angle of interest (angle A) and the right angle.
Once such a triangle is chosen, the sine of the angle is equal to the length of the opposite side, divided by the length of the hypotenuse:[2]
The other trigonometric functions of the angle can be defined similarly; for example, the tangent is the ratio between the opposite and adjacent sides.[2]
As stated, the values 

Unit circle definitions[edit]
In trigonometry, a unit circle is the circle of radius one centered at the origin (0, 0) in the Cartesian coordinate system.
Unit circle: a circle with radius one
Let a line through the origin intersect the unit circle, making an angle of θ with the positive half of the x-axis. The x— and y-coordinates of this point of intersection are equal to cos(θ) and sin(θ), respectively. This definition is consistent with the right-angled triangle definition of sine and cosine when 




Using the unit circle definition has the advantage that the angle can be extended to any real argument. This can also be achieved by requiring certain symmetries, and that sine be a periodic function.
Complex exponential function definitions[edit]
The exponential function 
These can be reversed to give Euler’s formula
When plotted on the complex plane, the function 

When 


When 


Differential equation definition[edit]






Series definitions[edit]
The sine function (blue) is closely approximated by its Taylor polynomial of degree 7 (pink) for a full cycle centered on the origin.
This animation shows how including more and more terms in the partial sum of its Taylor series approaches a sine curve.
The successive derivatives of sine, evaluated at zero, can be used to determine its Taylor series. Using only geometry and properties of limits, it can be shown that the derivative of sine is cosine, and that the derivative of cosine is the negative of sine. This means the successive derivatives of sin(x) are cos(x), -sin(x), -cos(x), sin(x), continuing to repeat those four functions. The (4n+k)-th derivative, evaluated at the point 0:
where the superscript represents repeated differentiation. This implies the following Taylor series expansion at x = 0. One can then use the theory of Taylor series to show that the following identities hold for all real numbers x (where x is the angle in radians):[3]
Taking the derivative of each term gives the Taylor series for cosine:
Continued fraction definitions[edit]
The sine function can also be represented as a generalized continued fraction:
The continued fraction representations can be derived from Euler’s continued fraction formula and express the real number values, both rational and irrational, of the sine and cosine functions.
Identities[edit]
Exact identities (using radians):
These apply for all values of 
Reciprocals[edit]
The reciprocal of sine is cosecant, i.e., the reciprocal of sin(A) is csc(A), or cosec(A). Cosecant gives the ratio of the length of the hypotenuse to the length of the opposite side. Similarly, the reciprocal of cosine is secant, which gives the ratio of the length of the hypotenuse to that of the adjacent side.
Inverses[edit]
The usual principal values of the arcsin(x) and arccos(x) functions graphed on the Cartesian plane
The inverse function of sine is arcsine (arcsin or asin) or inverse sine (sin−1). The inverse function of cosine is arccosine (arccos, acos, or cos−1). (The superscript of −1 in sin−1 and cos−1 denotes the inverse of a function, not exponentiation.) As sine and cosine are not injective, their inverses are not exact inverse functions, but partial inverse functions. For example, sin(0) = 0, but also sin(π) = 0, sin(2π) = 0 etc. It follows that the arcsine function is multivalued: arcsin(0) = 0, but also arcsin(0) = π, arcsin(0) = 2π, etc. When only one value is desired, the function may be restricted to its principal branch. With this restriction, for each x in the domain, the expression arcsin(x) will evaluate only to a single value, called its principal value. The standard range of principal values for arcsin is from −π/2 to π/2 and the standard range for arccos is from 0 to π.
where (for some integer k):
By definition, arcsin and arccos satisfy the equations:
and
Pythagorean trigonometric identity[edit]
The basic relationship between the sine and the cosine is the Pythagorean trigonometric identity:[1]
where sin2(x) means (sin(x))2.
Double angle formulas[edit]
Sine and cosine satisfy the following double angle formulas:
Sine function in blue and sine squared function in red. The X axis is in radians.
The cosine double angle formula implies that sin2 and cos2 are, themselves, shifted and scaled sine waves. Specifically,[4]
The graph shows both the sine function and the sine squared function, with the sine in blue and sine squared in red. Both graphs have the same shape, but with different ranges of values, and different periods. Sine squared has only positive values, but twice the number of periods.
Derivative and integrals[edit]
The derivatives of sine and cosine are:
and their antiderivatives are:
where C denotes the constant of integration.[1]
Properties relating to the quadrants[edit]
The four quadrants of a Cartesian coordinate system
The table below displays many of the key properties of the sine function (sign, monotonicity, convexity), arranged by the quadrant of the argument. For arguments outside those in the table, one may compute the corresponding information by using the periodicity 
| Quadrant | Angle | Sine | Cosine | |||||
|---|---|---|---|---|---|---|---|---|
| Degrees | Radians | Sign | Monotony | Convexity | Sign | Monotony | Convexity | |
| 1st quadrant, I | 
|

|

|
increasing | concave | 
|
decreasing | concave |
| 2nd quadrant, II | 
|

|

|
decreasing | concave | 
|
decreasing | convex |
| 3rd quadrant, III | 
|

|

|
decreasing | convex | 
|
increasing | convex |
| 4th quadrant, IV | 
|

|

|
increasing | convex | 
|
increasing | concave |
The following table gives basic information at the boundary of the quadrants.
| Degrees | Radians | 
|

|
||
|---|---|---|---|---|---|
| Value | Point type | Value | Point type | ||

|

|

|
Root, inflection | 
|
Maximum |

|

|

|
Maximum | 
|
Root, inflection |

|

|

|
Root, inflection | 
|
Minimum |

|

|

|
Minimum | 
|
Root, inflection |
Fixed points[edit]
The fixed point iteration xn+1 = cos(xn) with initial value x0 = −1 converges to the Dottie number.
Zero is the only real fixed point of the sine function; in other words the only intersection of the sine function and the identity function is 


Arc length[edit]
The arc length of the sine curve between 

where 

The arc length for a full period is[6]
where 

Law of sines[edit]
The law of sines states that for an arbitrary triangle with sides a, b, and c and angles opposite those sides A, B and C:
This is equivalent to the equality of the first three expressions below:
where R is the triangle’s circumradius.
It can be proved by dividing the triangle into two right ones and using the above definition of sine. The law of sines is useful for computing the lengths of the unknown sides in a triangle if two angles and one side are known. This is a common situation occurring in triangulation, a technique to determine unknown distances by measuring two angles and an accessible enclosed distance.
Law of cosines[edit]
The law of cosines states that for an arbitrary triangle with sides a, b, and c and angles opposite those sides A, B and C:
In the case where 


Special values[edit]
Some common angles (θ) shown on the unit circle. The angles are given in degrees and radians, together with the corresponding intersection point on the unit circle, (cos(θ), sin(θ)).
For certain integral numbers x of degrees, the values of sin(x) and cos(x) are particularly simple and can be expressed without nested square roots. A table of these angles is given below. For more complex angle expressions see Exact trigonometric values § Common angles.
| Angle, x | sin(x) | cos(x) | |||||
|---|---|---|---|---|---|---|---|
| Degrees | Radians | Gradians | Turns | Exact | Decimal | Exact | Decimal |
| 0° | 0 | 0g | 0 | 0 | 0 | 1 | 1 |
| 15° | 1/12π | 16+2/3g | 1/24 | 
|
0.2588 | 
|
0.9659 |
| 30° | 1/6π | 33+1/3g | 1/12 | 1/2 | 0.5 | 
|
0.8660 |
| 45° | 1/4π | 50g | 1/8 | 
|
0.7071 | 
|
0.7071 |
| 60° | 1/3π | 66+2/3g | 1/6 | 
|
0.8660 | 1/2 | 0.5 |
| 75° | 5/12π | 83+1/3g | 5/24 | 
|
0.9659 | 
|
0.2588 |
| 90° | 1/2π | 100g | 1/4 | 1 | 1 | 0 | 0 |
90 degree increments:
| x in degrees | 0° | 90° | 180° | 270° | 360° |
|---|---|---|---|---|---|
| x in radians | 0 | π/2 | π | 3π/2 | 2π |
| x in gons | 0 | 100g | 200g | 300g | 400g |
| x in turns | 0 | 1/4 | 1/2 | 3/4 | 1 |
| sin x | 0 | 1 | 0 | −1 | 0 |
| cos x | 1 | 0 | −1 | 0 | 1 |
Relationship to complex numbers[edit]



Sine and cosine are used to connect the real and imaginary parts of a complex number with its polar coordinates (r, φ):
The real and imaginary parts are:
where r and φ represent the magnitude and angle of the complex number z.
For any real number θ, Euler’s formula says that:
Therefore, if the polar coordinates of z are (r, φ), 
Complex arguments[edit]
Domain coloring of sin(z) in the complex plane. Brightness indicates absolute magnitude, hue represents complex argument.
Applying the series definition of the sine and cosine to a complex argument, z, gives:
where sinh and cosh are the hyperbolic sine and cosine. These are entire functions.
It is also sometimes useful to express the complex sine and cosine functions in terms of the real and imaginary parts of its argument:
Partial fraction and product expansions of complex sine[edit]
Using the partial fraction expansion technique in complex analysis, one can find that the infinite series
both converge and are equal to 
Using product expansion technique, one can derive
Alternatively, the infinite product for the sine can be proved using complex Fourier series.
Usage of complex sine[edit]
sin(z) is found in the functional equation for the Gamma function,
which in turn is found in the functional equation for the Riemann zeta-function,
As a holomorphic function, sin z is a 2D solution of Laplace’s equation:
The complex sine function is also related to the level curves of pendulums.[how?][9][better source needed]
Complex graphs[edit]
|
|
|
|
| real component | imaginary component | magnitude |
|
|
|
|
| real component | imaginary component | magnitude |
History[edit]
While the early study of trigonometry can be traced to antiquity, the trigonometric functions as they are in use today were developed in the medieval period. The chord function was discovered by Hipparchus of Nicaea (180–125 BCE) and Ptolemy of Roman Egypt (90–165 CE). See in particular Ptolemy’s table of chords.
The sine and cosine functions can be traced to the jyā and koṭi-jyā functions used in Indian astronomy during the Gupta period (Aryabhatiya and Surya Siddhanta), via translation from Sanskrit to Arabic and then from Arabic to Latin.[10]
All six trigonometric functions in current use were known in Islamic mathematics by the 9th century, as was the law of sines, used in solving triangles.[11] With the exception of the sine (which was adopted from Indian mathematics), the other five modern trigonometric functions were discovered by Arabic mathematicians, including the cosine, tangent, cotangent, secant and cosecant.[11] Al-Khwārizmī (c. 780–850) produced tables of sines, cosines and tangents.[12][13] Muhammad ibn Jābir al-Harrānī al-Battānī (853–929) discovered the reciprocal functions of secant and cosecant, and produced the first table of cosecants for each degree from 1° to 90°.[13]
The first published use of the abbreviations sin, cos, and tan is by the 16th-century French mathematician Albert Girard; these were further promulgated by Euler (see below). The Opus palatinum de triangulis of Georg Joachim Rheticus, a student of Copernicus, was probably the first in Europe to define trigonometric functions directly in terms of right triangles instead of circles, with tables for all six trigonometric functions; this work was finished by Rheticus’ student Valentin Otho in 1596.
In a paper published in 1682, Leibniz proved that sin x is not an algebraic function of x.[14] Roger Cotes computed the derivative of sine in his Harmonia Mensurarum (1722).[15] Leonhard Euler’s Introductio in analysin infinitorum (1748) was mostly responsible for establishing the analytic treatment of trigonometric functions in Europe, also defining them as infinite series and presenting «Euler’s formula», as well as the near-modern abbreviations sin., cos., tang., cot., sec., and cosec.[10]
Etymology[edit]
Etymologically, the word sine derives from the Sanskrit word jyā ‘bow-string’[16][17]
or more specifically its synonym jīvá (both adopted from Ancient Greek χορδή ‘string’[18]), due to visual similarity between the arc of a circle with its corresponding chord and a bow with its string (see jyā, koti-jyā and utkrama-jyā). This was transliterated in Arabic as jība, which is however meaningless in that language and abbreviated jb (جب). Since Arabic is written without short vowels, jb was interpreted as the homograph jaib, jayb (جيب), which means ‘bosom’, ‘pocket’, ‘fold’. When the Arabic texts of Al-Battani and al-Khwārizmī were translated into Medieval Latin in the 12th century by Gerard of Cremona, he used the Latin equivalent sinus (which also means ‘bay’ or ‘fold’, and more specifically ‘the hanging fold of a toga over the breast’).[10][19][20] Gerard was probably not the first scholar to use this translation; Robert of Chester appears to have preceded him and there is evidence of even earlier usage.[21][22] The English form sine was introduced in the 1590s.[23]
The word cosine derives from an abbreviation of the Latin complementi sinus ‘sine of the complementary angle’ as cosinus in Edmund Gunter’s Canon triangulorum (1620), which also includes a similar definition of cotangens.[24][25][26]
Software implementations[edit]
There is no standard algorithm for calculating sine and cosine. IEEE 754, the most widely used standard for the specification of reliable floating-point computation, does not address calculating trigonometric functions such as sine. The reason is that no efficient algorithm is known for computing sine and cosine with a specified accuracy, especially for large inputs.[27]
Algorithms for calculating sine may be balanced for such constraints as speed, accuracy, portability, or range of input values accepted. This can lead to different results for different algorithms, especially for special circumstances such as very large inputs, e.g. sin(1022).
A common programming optimization, used especially in 3D graphics, is to pre-calculate a table of sine values, for example one value per degree, then for values in-between pick the closest pre-calculated value, or linearly interpolate between the 2 closest values to approximate it. This allows results to be looked up from a table rather than being calculated in real time. With modern CPU architectures this method may offer no advantage.[citation needed]
The CORDIC algorithm is commonly used in scientific calculators.
The sine and cosine functions, along with other trigonometric functions, is widely available across programming languages and platforms. In computing, they are typically abbreviated to sin and cos.
Some CPU architectures have a built-in instruction for sine, including the Intel x87 FPUs since the 80387.
In programming languages, sin and cos are typically either a built-in function or found within the language’s standard math library.
For example, the C standard library defines sine functions within math.h: sin(double), sinf(float), and sinl(long double). The parameter of each is a floating point value, specifying the angle in radians. Each function returns the same data type as it accepts. Many other trigonometric functions are also defined in math.h, such as for cosine, arc sine, and hyperbolic sine (sinh).
Similarly, Python defines math.sin(x) and math.cos(x) within the built-in math module. Complex sine and cosine functions are also available within the cmath module, e.g. cmath.sin(z). CPython’s math functions call the C math library, and use a double-precision floating-point format.
Turns based implementations[edit]
Some software libraries provide implementations of sine and cosine using the input angle in half-turns, a half-turn being an angle of 180 degrees or 
sinpi and cospi.[28][30][29][31][32][33] For example, sinpi(x) would evaluate to 
The accuracy advantage stems from the ability to perfectly represent key angles like full-turn, half-turn, and quarter-turn losslessly in binary floating-point or fixed-point. In contrast, representing 


Turns also have an accuracy advantage and efficiency advantage for computing modulo to one period. Computing modulo 1 turn or modulo 2 half-turns can be losslessly and efficiently computed in both floating-point and fixed-point. For example, computing modulo 1 or modulo 2 for a binary point scaled fixed-point value requires only a bit shift or bitwise AND operation. In contrast, computing modulo 

For applications involving angle sensors, the sensor typically provides angle measurements in a form directly compatible with turns or half-turns. For example, an angle sensor may count from 0 to 4096 over one complete revolution.[34] If half-turns are used as the unit for angle, then the value provided by the sensor directly and losslessly maps to a fixed-point data type with 11 bits to the right of the binary point. In contrast, if radians are used as the unit for storing the angle, then the inaccuracies and cost of multiplying the raw sensor integer by an approximation to 
See also[edit]
- Āryabhaṭa’s sine table
- Bhaskara I’s sine approximation formula
- Discrete sine transform
- Euler’s formula
- Generalized trigonometry
- Hyperbolic function
- Dixon elliptic functions
- Lemniscate elliptic functions
- Law of sines
- List of periodic functions
- List of trigonometric identities
- Madhava series
- Madhava’s sine table
- Optical sine theorem
- Polar sine—a generalization to vertex angles
- Proofs of trigonometric identities
- Sinc function
- Sine and cosine transforms
- Sine integral
- Sine quadrant
- Sine wave
- Sine–Gordon equation
- Sinusoidal model
- SOH-CAH-TOA
- Trigonometric functions
- Trigonometric integral
Citations[edit]
- ^ a b c Weisstein, Eric W. «Sine». mathworld.wolfram.com. Retrieved 2020-08-29.
- ^ a b «Sine, Cosine, Tangent». www.mathsisfun.com. Retrieved 2020-08-29.
- ^ See Ahlfors, pages 43–44.
- ^ «Sine-squared function». Retrieved August 9, 2019.
- ^ «OEIS A003957». oeis.org. Retrieved 2019-05-26.
- ^ a b «A105419 — Oeis».
- ^ Adlaj, Semjon (2012). «An Eloquent Formula for the Perimeter of an Ellipse» (PDF). American Mathematical Society. p. 1097.
- ^ Rudin, Walter (1987). Real and Complex Analysis (Third ed.). McGraw-Hill Book Company. ISBN 0-07-100276-6. p. 299, Theorem 15.4
- ^ «Why are the phase portrait of the simple plane pendulum and a domain coloring of sin(z) so similar?». math.stackexchange.com. Retrieved 2019-08-12.
- ^ a b c Merzbach, Uta C.; Boyer, Carl B. (2011), A History of Mathematics (3rd ed.), John Wiley & Sons: It was Robert of Chester’s translation from the Arabic that resulted in our word «sine». The Hindus had given the name jiva to the half-chord in trigonometry, and the Arabs had taken this over as jiba. In the Arabic language there is also the word jaib meaning «bay» or «inlet». When Robert of Chester came to translate the technical word jiba, he seems to have confused this with the word jaib (perhaps because vowels were omitted); hence, he used the word sinus, the Latin word for «bay» or «inlet».
- ^ a b Gingerich, Owen (1986). «Islamic Astronomy». Scientific American. Vol. 254. p. 74. Archived from the original on 2013-10-19. Retrieved 2010-07-13.
- ^ Jacques Sesiano, «Islamic mathematics», p. 157, in Selin, Helaine; D’Ambrosio, Ubiratan, eds. (2000). Mathematics Across Cultures: The History of Non-western Mathematics. Springer Science+Business Media. ISBN 978-1-4020-0260-1.
- ^ a b «trigonometry». Encyclopedia Britannica.
- ^ Nicolás Bourbaki (1994). Elements of the History of Mathematics. Springer. ISBN 9783540647676.
- ^ «Why the sine has a simple derivative Archived 2011-07-20 at the Wayback Machine», in Historical Notes for Calculus Teachers Archived 2011-07-20 at the Wayback Machine by V. Frederick Rickey Archived 2011-07-20 at the Wayback Machine
- ^ «How the Trig Functions Got their Names». Ask Dr. Math. Drexel University. Retrieved 2 March 2010.
- ^ J J O’Connor and E F Robertson (June 1996). «The trigonometric functions». Retrieved 2 March 2010.
- ^ See Plofker, Mathematics in India, Princeton University Press, 2009, p. 257
See «Clark University». Archived from the original on 15 June 2008.
See Maor (1998), chapter 3, regarding the etymology. - ^ Eli Maor (1998), Trigonometric Delights, Princeton: Princeton University Press, p. 35-36.
- ^ Victor J. Katz (2008), A History of Mathematics, Boston: Addison-Wesley, 3rd. ed., p. 253, sidebar 8.1. «A History of Mathematics» (PDF). Archived (PDF) from the original on 2015-04-14. Retrieved 2015-04-09.: The English word “sine” comes from a series of mistranslations of the Sanskrit jyā-ardha (chord-half). Āryabhaṭa frequently abbreviated this term to jyā or its synonym jīvá. When some of the Hindu works were later translated into Arabic, the word was simply transcribed phonetically into an otherwise meaningless Arabic word jiba. But since Arabic is written without vowels, later writers interpreted the consonants jb as jaib, which means bosom or breast. In the twelfth century, when an Arabic trigonometry work was translated into Latin, the translator used the equivalent Latin word sinus, which also meant bosom, and by extension, fold (as in a toga over a breast), or a bay or gulf.
- ^ Smith, D.E. (1958) [1925], History of Mathematics, vol. I, Dover, p. 202, ISBN 0-486-20429-4
- ^ Various sources credit the first use of sinus to either
- Plato Tiburtinus’s 1116 translation of the Astronomy of Al-Battani
- Gerard of Cremona’s translation of the Algebra of al-Khwārizmī
- Robert of Chester’s 1145 translation of the tables of al-Khwārizmī
See Merlet, A Note on the History of the Trigonometric Functions in Ceccarelli (ed.), International Symposium on History of Machines and Mechanisms, Springer, 2004
See Maor (1998), chapter 3, for an earlier etymology crediting Gerard.
See Katx, Victor (July 2008). A history of mathematics (3rd ed.). Boston: Pearson. p. 210 (sidebar). ISBN 978-0321387004. - ^ The anglicized form is first recorded in 1593 in Thomas Fale’s Horologiographia, the Art of Dialling.
- ^ Gunter, Edmund (1620). Canon triangulorum.
- ^ Roegel, Denis, ed. (6 December 2010). «A reconstruction of Gunter’s Canon triangulorum (1620)» (Research report). HAL. inria-00543938. Archived from the original on 28 July 2017. Retrieved 28 July 2017.
- ^ «cosine».
- ^ Zimmermann, Paul (2006), «Can we trust floating-point numbers?», Grand Challenges of Informatics (PDF), p. 14/31, archived (PDF) from the original on 2011-07-16, retrieved 2010-09-11
- ^ a b «MATLAB Documentation sinpi
- ^ a b «R Documentation sinpi
- ^ «OpenCL Documentation sinpi
- ^ «Julia Documentation sinpi
- ^ «CUDA Documentation sinpi
- ^ «ARM Documentation sinpi
- ^ «ALLEGRO Angle Sensor Datasheet
References[edit]
- Traupman, Ph.D., John C. (1966), The New College Latin & English Dictionary, Toronto: Bantam, ISBN 0-553-27619-0
- Webster’s Seventh New Collegiate Dictionary, Springfield: G. & C. Merriam Company, 1969
External links[edit]
Look up sine in Wiktionary, the free dictionary.
Media related to Sine function at Wikimedia Commons
| Sine and cosine | |
|---|---|
 |
|
| General information | |
| General definition | ![{displaystyle {begin{aligned}&sin(alpha )={frac {textrm {opposite}}{textrm {hypotenuse}}}\[8pt]&cos(alpha )={frac {textrm {adjacent}}{textrm {hypotenuse}}}\[8pt]end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ea2762f231f5fdc1dcfacd59c303106f596ab2e1) |
| Fields of application | Trigonometry, Fourier series, etc. |
In mathematics, sine and cosine are trigonometric functions of an angle. The sine and cosine of an acute angle are defined in the context of a right triangle: for the specified angle, its sine is the ratio of the length of the side that is opposite that angle to the length of the longest side of the triangle (the hypotenuse), and the cosine is the ratio of the length of the adjacent leg to that of the hypotenuse. For an angle 


More generally, the definitions of sine and cosine can be extended to any real value in terms of the lengths of certain line segments in a unit circle. More modern definitions express the sine and cosine as infinite series, or as the solutions of certain differential equations, allowing their extension to arbitrary positive and negative values and even to complex numbers.
The sine and cosine functions are commonly used to model periodic phenomena such as sound and light waves, the position and velocity of harmonic oscillators, sunlight intensity and day length, and average temperature variations throughout the year. They can be traced to the jyā and koṭi-jyā functions used in Indian astronomy during the Gupta period.
Notation[edit]
Sine and cosine are written using functional notation with the abbreviations sin and cos.
Often, if the argument is simple enough, the function value will be written without parentheses, as sin θ rather than as sin(θ).
Each of sine and cosine is a function of an angle, which is usually expressed in terms of radians or degrees. Except where explicitly stated otherwise, this article assumes that the angle is measured in radians.
Definitions[edit]
Right-angled triangle definitions[edit]
For the angle α, the sine function gives the ratio of the length of the opposite side to the length of the hypotenuse.
To define the sine and cosine of an acute angle α, start with a right triangle that contains an angle of measure α; in the accompanying figure, angle α in triangle ABC is the angle of interest. The three sides of the triangle are named as follows:
- The opposite side is the side opposite to the angle of interest, in this case side a.
- The hypotenuse is the side opposite the right angle, in this case side h. The hypotenuse is always the longest side of a right-angled triangle.
- The adjacent side is the remaining side, in this case side b. It forms a side of (and is adjacent to) both the angle of interest (angle A) and the right angle.
Once such a triangle is chosen, the sine of the angle is equal to the length of the opposite side, divided by the length of the hypotenuse:[2]
The other trigonometric functions of the angle can be defined similarly; for example, the tangent is the ratio between the opposite and adjacent sides.[2]
As stated, the values 

Unit circle definitions[edit]
In trigonometry, a unit circle is the circle of radius one centered at the origin (0, 0) in the Cartesian coordinate system.
Unit circle: a circle with radius one
Let a line through the origin intersect the unit circle, making an angle of θ with the positive half of the x-axis. The x— and y-coordinates of this point of intersection are equal to cos(θ) and sin(θ), respectively. This definition is consistent with the right-angled triangle definition of sine and cosine when 




Using the unit circle definition has the advantage that the angle can be extended to any real argument. This can also be achieved by requiring certain symmetries, and that sine be a periodic function.
Complex exponential function definitions[edit]
The exponential function 
These can be reversed to give Euler’s formula
When plotted on the complex plane, the function 

When 


When 


Differential equation definition[edit]






Series definitions[edit]
The sine function (blue) is closely approximated by its Taylor polynomial of degree 7 (pink) for a full cycle centered on the origin.
This animation shows how including more and more terms in the partial sum of its Taylor series approaches a sine curve.
The successive derivatives of sine, evaluated at zero, can be used to determine its Taylor series. Using only geometry and properties of limits, it can be shown that the derivative of sine is cosine, and that the derivative of cosine is the negative of sine. This means the successive derivatives of sin(x) are cos(x), -sin(x), -cos(x), sin(x), continuing to repeat those four functions. The (4n+k)-th derivative, evaluated at the point 0:
where the superscript represents repeated differentiation. This implies the following Taylor series expansion at x = 0. One can then use the theory of Taylor series to show that the following identities hold for all real numbers x (where x is the angle in radians):[3]
Taking the derivative of each term gives the Taylor series for cosine:
Continued fraction definitions[edit]
The sine function can also be represented as a generalized continued fraction:
The continued fraction representations can be derived from Euler’s continued fraction formula and express the real number values, both rational and irrational, of the sine and cosine functions.
Identities[edit]
Exact identities (using radians):
These apply for all values of 
Reciprocals[edit]
The reciprocal of sine is cosecant, i.e., the reciprocal of sin(A) is csc(A), or cosec(A). Cosecant gives the ratio of the length of the hypotenuse to the length of the opposite side. Similarly, the reciprocal of cosine is secant, which gives the ratio of the length of the hypotenuse to that of the adjacent side.
Inverses[edit]
The usual principal values of the arcsin(x) and arccos(x) functions graphed on the Cartesian plane
The inverse function of sine is arcsine (arcsin or asin) or inverse sine (sin−1). The inverse function of cosine is arccosine (arccos, acos, or cos−1). (The superscript of −1 in sin−1 and cos−1 denotes the inverse of a function, not exponentiation.) As sine and cosine are not injective, their inverses are not exact inverse functions, but partial inverse functions. For example, sin(0) = 0, but also sin(π) = 0, sin(2π) = 0 etc. It follows that the arcsine function is multivalued: arcsin(0) = 0, but also arcsin(0) = π, arcsin(0) = 2π, etc. When only one value is desired, the function may be restricted to its principal branch. With this restriction, for each x in the domain, the expression arcsin(x) will evaluate only to a single value, called its principal value. The standard range of principal values for arcsin is from −π/2 to π/2 and the standard range for arccos is from 0 to π.
where (for some integer k):
By definition, arcsin and arccos satisfy the equations:
and
Pythagorean trigonometric identity[edit]
The basic relationship between the sine and the cosine is the Pythagorean trigonometric identity:[1]
where sin2(x) means (sin(x))2.
Double angle formulas[edit]
Sine and cosine satisfy the following double angle formulas:
Sine function in blue and sine squared function in red. The X axis is in radians.
The cosine double angle formula implies that sin2 and cos2 are, themselves, shifted and scaled sine waves. Specifically,[4]
The graph shows both the sine function and the sine squared function, with the sine in blue and sine squared in red. Both graphs have the same shape, but with different ranges of values, and different periods. Sine squared has only positive values, but twice the number of periods.
Derivative and integrals[edit]
The derivatives of sine and cosine are:
and their antiderivatives are:
where C denotes the constant of integration.[1]
Properties relating to the quadrants[edit]
The four quadrants of a Cartesian coordinate system
The table below displays many of the key properties of the sine function (sign, monotonicity, convexity), arranged by the quadrant of the argument. For arguments outside those in the table, one may compute the corresponding information by using the periodicity 
| Quadrant | Angle | Sine | Cosine | |||||
|---|---|---|---|---|---|---|---|---|
| Degrees | Radians | Sign | Monotony | Convexity | Sign | Monotony | Convexity | |
| 1st quadrant, I | 
|

|

|
increasing | concave | 
|
decreasing | concave |
| 2nd quadrant, II | 
|

|

|
decreasing | concave | 
|
decreasing | convex |
| 3rd quadrant, III | 
|

|

|
decreasing | convex | 
|
increasing | convex |
| 4th quadrant, IV | 
|

|

|
increasing | convex | 
|
increasing | concave |
The following table gives basic information at the boundary of the quadrants.
| Degrees | Radians | 
|

|
||
|---|---|---|---|---|---|
| Value | Point type | Value | Point type | ||

|

|

|
Root, inflection | 
|
Maximum |

|

|

|
Maximum | 
|
Root, inflection |

|

|

|
Root, inflection | 
|
Minimum |

|

|

|
Minimum | 
|
Root, inflection |
Fixed points[edit]
The fixed point iteration xn+1 = cos(xn) with initial value x0 = −1 converges to the Dottie number.
Zero is the only real fixed point of the sine function; in other words the only intersection of the sine function and the identity function is 


Arc length[edit]
The arc length of the sine curve between 

where 

The arc length for a full period is[6]
where 

Law of sines[edit]
The law of sines states that for an arbitrary triangle with sides a, b, and c and angles opposite those sides A, B and C:
This is equivalent to the equality of the first three expressions below:
where R is the triangle’s circumradius.
It can be proved by dividing the triangle into two right ones and using the above definition of sine. The law of sines is useful for computing the lengths of the unknown sides in a triangle if two angles and one side are known. This is a common situation occurring in triangulation, a technique to determine unknown distances by measuring two angles and an accessible enclosed distance.
Law of cosines[edit]
The law of cosines states that for an arbitrary triangle with sides a, b, and c and angles opposite those sides A, B and C:
In the case where 


Special values[edit]
Some common angles (θ) shown on the unit circle. The angles are given in degrees and radians, together with the corresponding intersection point on the unit circle, (cos(θ), sin(θ)).
For certain integral numbers x of degrees, the values of sin(x) and cos(x) are particularly simple and can be expressed without nested square roots. A table of these angles is given below. For more complex angle expressions see Exact trigonometric values § Common angles.
| Angle, x | sin(x) | cos(x) | |||||
|---|---|---|---|---|---|---|---|
| Degrees | Radians | Gradians | Turns | Exact | Decimal | Exact | Decimal |
| 0° | 0 | 0g | 0 | 0 | 0 | 1 | 1 |
| 15° | 1/12π | 16+2/3g | 1/24 | 
|
0.2588 | 
|
0.9659 |
| 30° | 1/6π | 33+1/3g | 1/12 | 1/2 | 0.5 | 
|
0.8660 |
| 45° | 1/4π | 50g | 1/8 | 
|
0.7071 | 
|
0.7071 |
| 60° | 1/3π | 66+2/3g | 1/6 | 
|
0.8660 | 1/2 | 0.5 |
| 75° | 5/12π | 83+1/3g | 5/24 | 
|
0.9659 | 
|
0.2588 |
| 90° | 1/2π | 100g | 1/4 | 1 | 1 | 0 | 0 |
90 degree increments:
| x in degrees | 0° | 90° | 180° | 270° | 360° |
|---|---|---|---|---|---|
| x in radians | 0 | π/2 | π | 3π/2 | 2π |
| x in gons | 0 | 100g | 200g | 300g | 400g |
| x in turns | 0 | 1/4 | 1/2 | 3/4 | 1 |
| sin x | 0 | 1 | 0 | −1 | 0 |
| cos x | 1 | 0 | −1 | 0 | 1 |
Relationship to complex numbers[edit]



Sine and cosine are used to connect the real and imaginary parts of a complex number with its polar coordinates (r, φ):
The real and imaginary parts are:
where r and φ represent the magnitude and angle of the complex number z.
For any real number θ, Euler’s formula says that:
Therefore, if the polar coordinates of z are (r, φ), 
Complex arguments[edit]
Domain coloring of sin(z) in the complex plane. Brightness indicates absolute magnitude, hue represents complex argument.
Applying the series definition of the sine and cosine to a complex argument, z, gives:
where sinh and cosh are the hyperbolic sine and cosine. These are entire functions.
It is also sometimes useful to express the complex sine and cosine functions in terms of the real and imaginary parts of its argument:
Partial fraction and product expansions of complex sine[edit]
Using the partial fraction expansion technique in complex analysis, one can find that the infinite series
both converge and are equal to 
Using product expansion technique, one can derive
Alternatively, the infinite product for the sine can be proved using complex Fourier series.
Usage of complex sine[edit]
sin(z) is found in the functional equation for the Gamma function,
which in turn is found in the functional equation for the Riemann zeta-function,
As a holomorphic function, sin z is a 2D solution of Laplace’s equation:
The complex sine function is also related to the level curves of pendulums.[how?][9][better source needed]
Complex graphs[edit]
|
|
|
|
| real component | imaginary component | magnitude |
|
|
|
|
| real component | imaginary component | magnitude |
History[edit]
While the early study of trigonometry can be traced to antiquity, the trigonometric functions as they are in use today were developed in the medieval period. The chord function was discovered by Hipparchus of Nicaea (180–125 BCE) and Ptolemy of Roman Egypt (90–165 CE). See in particular Ptolemy’s table of chords.
The sine and cosine functions can be traced to the jyā and koṭi-jyā functions used in Indian astronomy during the Gupta period (Aryabhatiya and Surya Siddhanta), via translation from Sanskrit to Arabic and then from Arabic to Latin.[10]
All six trigonometric functions in current use were known in Islamic mathematics by the 9th century, as was the law of sines, used in solving triangles.[11] With the exception of the sine (which was adopted from Indian mathematics), the other five modern trigonometric functions were discovered by Arabic mathematicians, including the cosine, tangent, cotangent, secant and cosecant.[11] Al-Khwārizmī (c. 780–850) produced tables of sines, cosines and tangents.[12][13] Muhammad ibn Jābir al-Harrānī al-Battānī (853–929) discovered the reciprocal functions of secant and cosecant, and produced the first table of cosecants for each degree from 1° to 90°.[13]
The first published use of the abbreviations sin, cos, and tan is by the 16th-century French mathematician Albert Girard; these were further promulgated by Euler (see below). The Opus palatinum de triangulis of Georg Joachim Rheticus, a student of Copernicus, was probably the first in Europe to define trigonometric functions directly in terms of right triangles instead of circles, with tables for all six trigonometric functions; this work was finished by Rheticus’ student Valentin Otho in 1596.
In a paper published in 1682, Leibniz proved that sin x is not an algebraic function of x.[14] Roger Cotes computed the derivative of sine in his Harmonia Mensurarum (1722).[15] Leonhard Euler’s Introductio in analysin infinitorum (1748) was mostly responsible for establishing the analytic treatment of trigonometric functions in Europe, also defining them as infinite series and presenting «Euler’s formula», as well as the near-modern abbreviations sin., cos., tang., cot., sec., and cosec.[10]
Etymology[edit]
Etymologically, the word sine derives from the Sanskrit word jyā ‘bow-string’[16][17]
or more specifically its synonym jīvá (both adopted from Ancient Greek χορδή ‘string’[18]), due to visual similarity between the arc of a circle with its corresponding chord and a bow with its string (see jyā, koti-jyā and utkrama-jyā). This was transliterated in Arabic as jība, which is however meaningless in that language and abbreviated jb (جب). Since Arabic is written without short vowels, jb was interpreted as the homograph jaib, jayb (جيب), which means ‘bosom’, ‘pocket’, ‘fold’. When the Arabic texts of Al-Battani and al-Khwārizmī were translated into Medieval Latin in the 12th century by Gerard of Cremona, he used the Latin equivalent sinus (which also means ‘bay’ or ‘fold’, and more specifically ‘the hanging fold of a toga over the breast’).[10][19][20] Gerard was probably not the first scholar to use this translation; Robert of Chester appears to have preceded him and there is evidence of even earlier usage.[21][22] The English form sine was introduced in the 1590s.[23]
The word cosine derives from an abbreviation of the Latin complementi sinus ‘sine of the complementary angle’ as cosinus in Edmund Gunter’s Canon triangulorum (1620), which also includes a similar definition of cotangens.[24][25][26]
Software implementations[edit]
There is no standard algorithm for calculating sine and cosine. IEEE 754, the most widely used standard for the specification of reliable floating-point computation, does not address calculating trigonometric functions such as sine. The reason is that no efficient algorithm is known for computing sine and cosine with a specified accuracy, especially for large inputs.[27]
Algorithms for calculating sine may be balanced for such constraints as speed, accuracy, portability, or range of input values accepted. This can lead to different results for different algorithms, especially for special circumstances such as very large inputs, e.g. sin(1022).
A common programming optimization, used especially in 3D graphics, is to pre-calculate a table of sine values, for example one value per degree, then for values in-between pick the closest pre-calculated value, or linearly interpolate between the 2 closest values to approximate it. This allows results to be looked up from a table rather than being calculated in real time. With modern CPU architectures this method may offer no advantage.[citation needed]
The CORDIC algorithm is commonly used in scientific calculators.
The sine and cosine functions, along with other trigonometric functions, is widely available across programming languages and platforms. In computing, they are typically abbreviated to sin and cos.
Some CPU architectures have a built-in instruction for sine, including the Intel x87 FPUs since the 80387.
In programming languages, sin and cos are typically either a built-in function or found within the language’s standard math library.
For example, the C standard library defines sine functions within math.h: sin(double), sinf(float), and sinl(long double). The parameter of each is a floating point value, specifying the angle in radians. Each function returns the same data type as it accepts. Many other trigonometric functions are also defined in math.h, such as for cosine, arc sine, and hyperbolic sine (sinh).
Similarly, Python defines math.sin(x) and math.cos(x) within the built-in math module. Complex sine and cosine functions are also available within the cmath module, e.g. cmath.sin(z). CPython’s math functions call the C math library, and use a double-precision floating-point format.
Turns based implementations[edit]
Some software libraries provide implementations of sine and cosine using the input angle in half-turns, a half-turn being an angle of 180 degrees or 
sinpi and cospi.[28][30][29][31][32][33] For example, sinpi(x) would evaluate to 
The accuracy advantage stems from the ability to perfectly represent key angles like full-turn, half-turn, and quarter-turn losslessly in binary floating-point or fixed-point. In contrast, representing 


Turns also have an accuracy advantage and efficiency advantage for computing modulo to one period. Computing modulo 1 turn or modulo 2 half-turns can be losslessly and efficiently computed in both floating-point and fixed-point. For example, computing modulo 1 or modulo 2 for a binary point scaled fixed-point value requires only a bit shift or bitwise AND operation. In contrast, computing modulo 

For applications involving angle sensors, the sensor typically provides angle measurements in a form directly compatible with turns or half-turns. For example, an angle sensor may count from 0 to 4096 over one complete revolution.[34] If half-turns are used as the unit for angle, then the value provided by the sensor directly and losslessly maps to a fixed-point data type with 11 bits to the right of the binary point. In contrast, if radians are used as the unit for storing the angle, then the inaccuracies and cost of multiplying the raw sensor integer by an approximation to 
See also[edit]
- Āryabhaṭa’s sine table
- Bhaskara I’s sine approximation formula
- Discrete sine transform
- Euler’s formula
- Generalized trigonometry
- Hyperbolic function
- Dixon elliptic functions
- Lemniscate elliptic functions
- Law of sines
- List of periodic functions
- List of trigonometric identities
- Madhava series
- Madhava’s sine table
- Optical sine theorem
- Polar sine—a generalization to vertex angles
- Proofs of trigonometric identities
- Sinc function
- Sine and cosine transforms
- Sine integral
- Sine quadrant
- Sine wave
- Sine–Gordon equation
- Sinusoidal model
- SOH-CAH-TOA
- Trigonometric functions
- Trigonometric integral
Citations[edit]
- ^ a b c Weisstein, Eric W. «Sine». mathworld.wolfram.com. Retrieved 2020-08-29.
- ^ a b «Sine, Cosine, Tangent». www.mathsisfun.com. Retrieved 2020-08-29.
- ^ See Ahlfors, pages 43–44.
- ^ «Sine-squared function». Retrieved August 9, 2019.
- ^ «OEIS A003957». oeis.org. Retrieved 2019-05-26.
- ^ a b «A105419 — Oeis».
- ^ Adlaj, Semjon (2012). «An Eloquent Formula for the Perimeter of an Ellipse» (PDF). American Mathematical Society. p. 1097.
- ^ Rudin, Walter (1987). Real and Complex Analysis (Third ed.). McGraw-Hill Book Company. ISBN 0-07-100276-6. p. 299, Theorem 15.4
- ^ «Why are the phase portrait of the simple plane pendulum and a domain coloring of sin(z) so similar?». math.stackexchange.com. Retrieved 2019-08-12.
- ^ a b c Merzbach, Uta C.; Boyer, Carl B. (2011), A History of Mathematics (3rd ed.), John Wiley & Sons: It was Robert of Chester’s translation from the Arabic that resulted in our word «sine». The Hindus had given the name jiva to the half-chord in trigonometry, and the Arabs had taken this over as jiba. In the Arabic language there is also the word jaib meaning «bay» or «inlet». When Robert of Chester came to translate the technical word jiba, he seems to have confused this with the word jaib (perhaps because vowels were omitted); hence, he used the word sinus, the Latin word for «bay» or «inlet».
- ^ a b Gingerich, Owen (1986). «Islamic Astronomy». Scientific American. Vol. 254. p. 74. Archived from the original on 2013-10-19. Retrieved 2010-07-13.
- ^ Jacques Sesiano, «Islamic mathematics», p. 157, in Selin, Helaine; D’Ambrosio, Ubiratan, eds. (2000). Mathematics Across Cultures: The History of Non-western Mathematics. Springer Science+Business Media. ISBN 978-1-4020-0260-1.
- ^ a b «trigonometry». Encyclopedia Britannica.
- ^ Nicolás Bourbaki (1994). Elements of the History of Mathematics. Springer. ISBN 9783540647676.
- ^ «Why the sine has a simple derivative Archived 2011-07-20 at the Wayback Machine», in Historical Notes for Calculus Teachers Archived 2011-07-20 at the Wayback Machine by V. Frederick Rickey Archived 2011-07-20 at the Wayback Machine
- ^ «How the Trig Functions Got their Names». Ask Dr. Math. Drexel University. Retrieved 2 March 2010.
- ^ J J O’Connor and E F Robertson (June 1996). «The trigonometric functions». Retrieved 2 March 2010.
- ^ See Plofker, Mathematics in India, Princeton University Press, 2009, p. 257
See «Clark University». Archived from the original on 15 June 2008.
See Maor (1998), chapter 3, regarding the etymology. - ^ Eli Maor (1998), Trigonometric Delights, Princeton: Princeton University Press, p. 35-36.
- ^ Victor J. Katz (2008), A History of Mathematics, Boston: Addison-Wesley, 3rd. ed., p. 253, sidebar 8.1. «A History of Mathematics» (PDF). Archived (PDF) from the original on 2015-04-14. Retrieved 2015-04-09.: The English word “sine” comes from a series of mistranslations of the Sanskrit jyā-ardha (chord-half). Āryabhaṭa frequently abbreviated this term to jyā or its synonym jīvá. When some of the Hindu works were later translated into Arabic, the word was simply transcribed phonetically into an otherwise meaningless Arabic word jiba. But since Arabic is written without vowels, later writers interpreted the consonants jb as jaib, which means bosom or breast. In the twelfth century, when an Arabic trigonometry work was translated into Latin, the translator used the equivalent Latin word sinus, which also meant bosom, and by extension, fold (as in a toga over a breast), or a bay or gulf.
- ^ Smith, D.E. (1958) [1925], History of Mathematics, vol. I, Dover, p. 202, ISBN 0-486-20429-4
- ^ Various sources credit the first use of sinus to either
- Plato Tiburtinus’s 1116 translation of the Astronomy of Al-Battani
- Gerard of Cremona’s translation of the Algebra of al-Khwārizmī
- Robert of Chester’s 1145 translation of the tables of al-Khwārizmī
See Merlet, A Note on the History of the Trigonometric Functions in Ceccarelli (ed.), International Symposium on History of Machines and Mechanisms, Springer, 2004
See Maor (1998), chapter 3, for an earlier etymology crediting Gerard.
See Katx, Victor (July 2008). A history of mathematics (3rd ed.). Boston: Pearson. p. 210 (sidebar). ISBN 978-0321387004. - ^ The anglicized form is first recorded in 1593 in Thomas Fale’s Horologiographia, the Art of Dialling.
- ^ Gunter, Edmund (1620). Canon triangulorum.
- ^ Roegel, Denis, ed. (6 December 2010). «A reconstruction of Gunter’s Canon triangulorum (1620)» (Research report). HAL. inria-00543938. Archived from the original on 28 July 2017. Retrieved 28 July 2017.
- ^ «cosine».
- ^ Zimmermann, Paul (2006), «Can we trust floating-point numbers?», Grand Challenges of Informatics (PDF), p. 14/31, archived (PDF) from the original on 2011-07-16, retrieved 2010-09-11
- ^ a b «MATLAB Documentation sinpi
- ^ a b «R Documentation sinpi
- ^ «OpenCL Documentation sinpi
- ^ «Julia Documentation sinpi
- ^ «CUDA Documentation sinpi
- ^ «ARM Documentation sinpi
- ^ «ALLEGRO Angle Sensor Datasheet
References[edit]
- Traupman, Ph.D., John C. (1966), The New College Latin & English Dictionary, Toronto: Bantam, ISBN 0-553-27619-0
- Webster’s Seventh New Collegiate Dictionary, Springfield: G. & C. Merriam Company, 1969
External links[edit]
Look up sine in Wiktionary, the free dictionary.
Media related to Sine function at Wikimedia Commons
тригонометрическая функция угла
| Синус | |
|---|---|
 |
|
| Основные характеристики | |
| Четность | нечетное |
| Домен | (- ∞, + ∞) |
| Кодомен | [−1, 1] |
| Период | 2π |
| Конкретные значения | |
| В нуле | 0 |
| Максимум | (2kπ + π / 2, 1) |
| Минимум | (2kπ — π / 2, −1) |
| Особенности | |
| Корень | kπ |
| Критическая точка | kπ + π / 2 |
| Перегиб точка | kπ |
| Фиксированная точка | 0 |
|
В математике синус — это тригонометрическая функция угла угла. Синус острого угла определяется в контексте прямоугольного треугольника : для указанного угла это отношение длины стороны, противоположной этому углу, к длине самой длинной стороны. треугольника (гипотенуза ). Для угла x { displaystyle x}

В более общем смысле определение синуса ( и другие тригонометрические функции) могут быть расширены до любого действительного значения с точки зрения длины определенного линейного сегмента в единичной окружности . Более современные определения выражают синус как бесконечный ряд или как решение некоторых дифференциальных уравнений, что позволяет их расширить до произвольных положительных и отрицательных значений и даже до комплексных чисел.
Синусоидальная функция обычно используется для моделирования периодических явлений, таких как звук и световые волны, положение и скорость гармонических осцилляторов, интенсивность солнечного света и продолжительность светового дня, а также изменения средней температуры на всем протяжении год.
Функциональный синус можно проследить до функций jyā и koṭi-jyā, используемых в период Гупта Индийская астрономия (Aryabhatiya, Сурья Сиддханта ), путем перевода с санскрита на арабский, а затем с арабского на латинский. Слово «синус» (латинское «синус») произошло от латинского неправильного перевода Робертом Честерским арабского джиба, который является транслитерацией санскрита. слово для половины хорды, джья-ардха.
Содержание
- 1 Определение прямоугольного треугольника
- 2 Определение единичного круга
- 3 Тождества
- 3.1 Взаимное
- 3.2 Обратное
- 3.3 Исчисление
- 3.4 Другие тригонометрические функции
- 3.5 Функция квадрата синуса
- 4 Свойства, относящиеся к квадрантам
- 5 Определение ряда
- 5.1 Непрерывная дробь
- 6 Фиксированная точка
- 7 Длина дуги
- 8 Закон синусов
- 9 Особые значения
- 10 Связь с комплексными числами
- 10.1 Синус с комплексным аргументом
- 10.1.1 Разложение комплексного синуса на частичную дробь и произведение
- 10.1.2 Использование комплексного sine
- 10.2 Сложные графы
- 10.1 Синус с комплексным аргументом
- 11 История
- 11.1 Этимология
- 12 Программные реализации
- 12.1 Реализации на основе поворотов
- 13 См. также
- 14 Цитаты
- 15 Ссылки
- 16 Внешние ссылки
прямоугольный треугольник определение угла

Чтобы определить функцию синуса острого угла α, начните с прямоугольный треугольник, содержащий угол измерения α; на сопроводительном рисунке угол α в треугольнике ABC представляет собой интересующий угол. Три стороны треугольника названы следующим образом:
- Противоположная сторона — это сторона, противоположная интересующему углу, в данном случае сторона a.
- Гипотенуза — это сторона, противоположная прямому углу, в эта сторона дела h. Гипотенуза всегда является самой длинной стороной прямоугольного треугольника.
- Соседняя сторона — это оставшаяся сторона, в данном случае сторона b. Он образует сторону (и примыкает) как к интересующему углу (углу A), так и к прямому углу.
После выбора такого треугольника синус угла равен длине противоположной стороны, деленное на длину гипотенузы:
- sin (α) = противоположная гипотенуза { displaystyle sin ( alpha) = { frac { textrm {Against}} { textrm {hypotenuse}}}}
Остальные тригонометрические функции угла можно определить аналогично; например, косинус угла — это отношение между соседней стороной и гипотенузой, а касательная дает отношение между противоположной и смежной сторонами.
Как указано, значение sin (α) { displaystyle sin ( alpha)}
Определение единичной окружности
В тригонометрии, единичная окружность — это окружность радиуса 1 с центром в начале координат (0, 0) в Декартова система координат.

Пусть прямая, проходящая через начало координат, пересекает единичную окружность, составляя угол θ с положительной половиной оси x. Координаты x и y этой точки пересечения равны cos (θ) и sin (θ) соответственно. Это определение согласуется с определением синуса и косинуса в прямоугольном треугольнике, когда 0 ° < θ < 90°: because the length of the hypotenuse of the unit circle is always 1, sin (θ) = противоположная гипотенуза = противоположная точка 1 = противоположная { displaystyle sin ( theta) = { tfrac { textrm {напротив}} { textrm {гипотенуза}}} = { tfrac { textrm {напротив}} {1}} = { textrm {напротив}}}


Использование определения единичной окружности имеет то преимущество, что угол может быть расширен до любого действительного аргумента. Этого также можно добиться, потребовав определенные симметрии, и чтобы синус был периодической функцией.
Анимация, показывающая, как функция синуса (красным) y = sin (θ) { displaystyle y = sin ( theta)}
строится по координате y (красная точка) точки на единичной окружности (зеленого цвета) под углом θ.
Идентификаторы
Точные идентификаторы (с использованием радиан ):
Они применяются для всех значений θ { displaystyle theta}
- sin (θ) знак равно соз (π 2 — θ) = 1 csc (θ) { displaystyle sin ( theta) = cos left ({ frac { pi} {2}} — theta right) = { frac {1} { csc ( theta)}}}
Взаимное
, обратное синуса — косеканс, т. е. обратное значение sin (A) это csc (A) или cosec (A). Косеканс дает отношение длины гипотенузы к длине противоположной стороны:
- csc (A) = 1 sin (A) = гипотенуза напротив = h a. { displaystyle csc (A) = { frac {1} { sin (A)}} = { frac { textrm {hypotenuse}} { textrm {напротив}}} = { frac {h} { a}}.}
Обратный

обратная функция синуса — это arcsine (arcsin или asin) или обратный синус (sin). Поскольку синус не является инъективным, это не точная обратная функция, а частичная обратная функция. Например, sin (0) = 0, но также sin (π) = 0, sin (2π) = 0 и т. Д. Отсюда следует, что функция арксинуса многозначна: arcsin (0) = 0, но также arcsin (0) = π, arcsin (0) = 2π и т. д. Когда требуется только одно значение, функция может быть ограничена ее главной ветвью. С этим ограничением для каждого x в домене выражение arcsin (x) будет оценивать только одно значение, называемое его главным значением.
- θ = arcsin (противоположная гипотенуза) = sin — 1 (ah). { displaystyle theta = arcsin left ({ frac { text {напротив}} { text {hypotenuse}}} right) = sin ^ {- 1} left ({ frac {a} { h}} right).}
где (для некоторого целого числа k):
- sin (y) = x ⟺ y = arcsin (x) + 2 π k, или y = π — arcsin ( Икс) + 2 π К { Displaystyle { begin {align} sin (y) = x iff y = arcsin (x) +2 pi k, { text {или}} \ y = pi — arcsin (x) +2 pi k end {align}}}
Или в одном уравнении:
- sin (y) = x ⟺ y = (- 1) k arcsin (x) + π К { displaystyle sin (y) = x iff y = (- 1) ^ {k} arcsin (x) + pi k}
По определению, арксинус удовлетворяет уравнению:
- sin (arcsin (x)) знак равно x { displaystyle sin ( arcsin (x)) = x !}
и
- arcsin (sin (θ)) = θ для — π 2 ≤ θ ≤ π 2. { displaystyle arcsin ( sin ( theta)) = theta quad { text {for}} — { frac { pi} {2}} leq theta leq { frac { pi} {2}}.}
Исчисление
Для функции синуса:
- f (x) = sin (x) { displaystyle f (x) = sin (x)}
Производная:
- f ‘(x) = cos (x) { displaystyle f’ (x) = cos (x)}
Первообразная:
- ∫ f (x) dx = — cos (x) + C { displaystyle int f (x) , dx = — cos (x) + C}
где C обозначает постоянную интегрирования.
Другие тригонометрические функции

sin (π / 2 — x) { displaystyle sin ( pi / 2-x)}

cos (x) { displaystyle cos (x)}

Любую тригонометрическую функцию можно выразить через любую другую (до знака плюс или минус или с помощью функции знака ).
В следующей таблице показано, как синус может быть выражен в терминах других общих тригонометрических функций :
| f θ | Использование плюса / минуса (±) | Использование функции знака (sgn) | |||||
|---|---|---|---|---|---|---|---|
| f θ = | ± на квадрант | f θ = | |||||
| I | II | III | IV | ||||
| соз | грех (θ) { displaystyle sin ( theta)} |
= ± 1 — cos 2 (θ) { displaystyle = pm { sqrt {1- cos ^ {2 } ( theta)}}} |
+ | + | − | − | = sign (соз (θ — π 2)) 1 — соз 2 (θ) { displaystyle = operatorname {sgn} left ( cos left ( theta — { frac { pi} {2}} right) right) { sqrt {1- cos ^ {2} ( theta)}}} |
cos (θ) { displaystyle соз ( theta)} |
= ± 1 — грех 2 (θ) { displaystyle = pm { sqrt {1- sin ^ {2} ( theta)}}} |
+ | − | − | + | = sgn (грех (θ + π 2)) 1 — грех 2 (θ) { displaystyle = operatorname {sgn} left ( sin left ( theta + { frac { pi} {2}} вправо) вправо) { sqrt {1- sin ^ {2} ( theta)}}} |
|
| кроватка | грех (θ) { displaystyle sin ( theta)} |
= ± 1 1 + детская кроватка 2 (θ) { displaysty le = pm { frac {1} { sqrt {1+ cot ^ {2} ( theta)}}}} |
+ | + | − | − | = sgn (детская кроватка (θ 2)) 1 1 + детская кроватка 2 (θ) { displaystyle = operatorname {sgn} left ( cot left ({ frac { theta} {2}} right) right) { frac {1} { sqrt {1+ кроватка ^ {2} ( theta)}}}} |
детская кроватка (θ) { displaystyle cot ( theta)} |
= ± 1 — sin 2 (θ) sin (θ) { displaystyle = pm { frac { sqrt {1- sin ^ {2} ( theta)}} { sin ( theta)}}} |
+ | − | − | + | = sgn (sin (θ + π 2)) 1 — грех 2 (θ) грех (θ) { displaystyle = operatorname {sgn} left ( sin left ( theta + { frac { pi} {2}} right) справа) { frac { sqrt {1- sin ^ {2} ( theta)}} { sin ( theta)}}} |
|
| tan | грех (θ) { displaystyle sin ( theta)} |
= ± загар (θ) 1 + загар 2 (θ) { displaystyle = pm { frac { tan ( theta)} { sqrt {1+ tan ^ { 2} ( theta)}}}} |
+ | − | − | + | = sign (tan (2 θ + π 4)) tan (θ) 1 + tan 2 (θ) { displaystyle = operatorname {sgn} left ( tan left ({ frac {2 theta + pi} {4}} right) right) { frac { tan ( theta)} { sqrt {1+ tan ^ {2 } ( theta)}}}} |
загар (θ) { Displaystyle загар ( theta)} |
= ± грех (θ) 1 — грех 2 (θ) { displaystyle = pm { frac { sin ( theta)} { sqrt {1- sin ^ {2} ( theta)}}}} |
+ | − | − | + | = sgn (sin (θ + π 2)) sin (θ) 1 — sin 2 (θ) { displaystyle = operatorname {sgn} left ( sin left ( theta + { frac { pi} {2}} right) right) { frac { sin ( theta)} { sqrt { 1- sin ^ {2} ( theta)}}}} |
|
| сек | грех (θ) { displaystyle sin ( theta)} |
= ± sec 2 (θ) — 1 сек (θ) { displaystyle = pm { frac { sqrt { sec ^ {2} ( theta) -1}} { sec ( theta)}}} |
+ | − | + | − | = sgn ( сек (4 θ — π 2)) сек 2 (θ) — 1 сек (θ) { displaystyle = operatorname {sgn} left ( sec left ({ frac {4 theta — pi } {2}} right) right) { frac { sqrt { sec ^ {2} ( theta) -1}} { sec ( theta)}}} |
сек (θ) { displaystyle sec ( theta)} |
= ± 1 1 — грех 2 (θ) { displaystyle = pm { frac {1} { sqrt {1- sin ^ {2} ( тета)}}}} |
+ | − | − | + | = знак (грех (θ + π 2)) 1 1 — грех 2 (θ) { displaystyle = operatorname {sgn} left ( sin left ( th eta + { frac { pi} {2}} right) right) { frac {1} { sqrt {1- sin ^ {2} ( theta)}}}} |
Для всех уравнения, которые используют плюс / минус (±), результат будет положительным для углов в первом квадранте.
Основное соотношение между синусом и косинусом также может быть выражено как тригонометрическое тождество Пифагора :
- cos 2 (θ) + sin 2 (θ) = 1 { displaystyle cos ^ {2} ( theta) + sin ^ {2} ( theta) = 1 !}
где sin (x) означает (sin (x)).
Функция синус-квадрата

На графике показаны как функция синуса, так и функция в квадрате синуса, причем синус отображается синим цветом, а синус в квадрате — красным. Оба графика имеют одинаковую форму, но с разными диапазонами значений и разными периодами. Синус в квадрате имеет только положительные значения, но в два раза больше периодов.
Функция квадрата синуса может быть выражена как модифицированная синусоида из тождества Пифагора и уменьшения мощности — с помощью формулы двойного угла косинуса:
- sin 2 (θ) = 1 — sin (2 θ + π 2) 2 { displaystyle sin ^ {2} ( theta) = { frac {1- sin (2 theta + { tfrac { pi} {2}})} {2} } }
Свойства, относящиеся к квадрантам

В таблице ниже показаны многие ключевые свойства синусоидальной функции (знак, монотонность, выпуклость), упорядоченные по квадрантам аргумента. Для аргументов, не указанных в таблице, можно вычислить соответствующую информацию, используя периодичность sin (α + 360 ∘) = sin (α) { displaystyle sin ( alpha +360 ^ { circ}) = sin ( alpha)}
| Квадрант | Градусы | Радианы | Значение | Знак | Монотонность | Выпуклость |
|---|---|---|---|---|---|---|
| 1-й квадрант | 0 ∘ < x < 90 ∘ {displaystyle 0^{circ } |
0 < x < π 2 {displaystyle 0 |
0 < sin ( x) < 1 {displaystyle 0<sin(x)<1} |
+ { displaystyle +} |
увеличение | вогнутый |
| 2-й квадрант | 90 ∘ < x < 180 ∘ {displaystyle 90^{circ } |
π 2 < x < π {displaystyle {frac {pi }{2}} |
0 < sin ( x) < 1 {displaystyle 0<sin(x)<1} |
+ { displaystyle +} |
уменьшение | вогнутый |
| 3-й квадрант | 180 ∘ < x < 270 ∘ {displaystyle 180^{circ } |
π < x < 3 π 2 {displaystyle pi  |
— 1 < sin ( x) < 0 {displaystyle -1<sin(x)<0} |
— { displaystyle -} |
уменьшение | выпуклый |
| 4-й квадрант | 270 ∘ < x < 360 ∘ {displaystyle 270^{circ } |
3 π 2 < x < 2 π {displaystyle {frac {3pi }{2}} |
— 1 < sin ( x) < 0 {displaystyle -1<sin(x)<0} |
— { displaystyle -} |
увеличение | выпуклое |

В следующей таблице приведены основная информация на границе квадрантов.
| Градусы | Радианы | грех (x) { displaystyle sin (x)} |
Тип точки |
|---|---|---|---|
0 ∘ { displaystyle 0 ^ { circ}} |
0 { displaystyle 0} |
0 { displaystyle 0} |
Корень, Inflection |
90 ∘ { displaystyle 90 ^ { circ}} |
π 2 { displaystyle { frac { pi} {2}}} |
1 { displaystyle 1} |
Максимум |
180 ∘ { displaystyle 180 ^ { circ}} |
π { displaystyle pi} |
0 { displaystyle 0} |
Корень, перегиб |
270 ∘ { displaystyle 270 ^ { circ}} |
3 π 2 { displaystyle { frac {3 pi } {2}}} |
— 1 { displaystyle -1} |
Минимум |
Определение ряда


Использование только геометрии и свойств ограничивает, можно показать, что производная синуса является косинусом, и что де Производная косинуса является отрицательной величиной синуса.
Использование отражения из вычисленного геометрического вывода синуса с (4n + k) -й производной в точке 0:
- sin (4 n + k) (0) = {0 когда k = 0 1, когда k = 1 0, когда k = 2 — 1, когда k = 3 { displaystyle sin ^ {(4n + k)} (0) = { begin {cases} 0 { text {when} } k = 0 \ 1 { text {when}} k = 1 \ 0 { text {when}} k = 2 \ — 1 { text {when}} k = 3 end {cases}} }
Это дает следующее разложение в ряд Тейлора при x = 0. Затем можно использовать теорию ряда Тейлора, чтобы показать, что следующие тождества выполняются для всех действительных чисел x ( где x — угол в радианах):
- sin (x) = x — x 3 3! + х 5 5! — х 7 7! + ⋯ знак равно ∑ N знак равно 0 ∞ (- 1) N (2 N + 1)! Икс 2 N + 1 { Displaystyle { begin {align} sin (x) = x — { frac {x ^ {3}} {3!}} + { frac {x ^ {5}} { 5!}} — { frac {x ^ {7}} {7!}} + Cdots \ [8pt] = sum _ {n = 0} ^ { infty} { frac {(-1) ^ {n}} {(2n + 1)!}} x ^ {2n + 1} \ [8pt] end {align}}}
Если бы x был выражен в градусах, тогда ряд содержал бы факторы, включающие степени π / 180: если x — количество градусов, количество радианов равно y = πx / 180, поэтому
- sin (xdeg) = sin (yrad) = π 180 x — (π 180) 3 х 3 3! + (π 180) 5 х 5 5! — (π 180) 7 х 7 7! + ⋯. { displaystyle { begin {align} sin (x _ { mathrm {deg}}) = sin (y _ { mathrm {rad}}) \ = { frac { pi} {180}} x- left ({ frac { pi} {180}} right) ^ {3} { frac {x ^ {3}} {3!}} + left ({ frac { pi} { 180}} right) ^ {5} { frac {x ^ {5}} {5!}} — left ({ frac { pi} {180}} right) ^ {7} { frac {x ^ {7}} {7!}} + cdots. end {align}}}
Формулы ряда для синуса и косинуса определяются однозначно, с точностью до выбора единицы для углов, согласно требованиям, что
- sin (0) = 0 и sin (2 x) = 2 sin (x) cos (x) cos 2 (x) + sin 2 (x) = 1 и соз (2 Икс) знак равно соз 2 (Икс) — грех 2 (Икс) { Displaystyle { begin {align} sin (0) = 0 { text {и}} sin (2x) = 2 sin (x) cos (x) \ cos ^ {2} (x) + sin ^ {2} (x) = 1 { text {and}} cos (2x) = cos ^ {2} (x) — sin ^ {2} (x) \ end {align}}}
Радиан — это единица, которая приводит к разложению с ведущим коэффициентом 1 для синуса и определяется дополнительное требование:
- sin (x) ≈ x, когда x ≈ 0. { displaystyle sin (x) приблизительно x { text {when}} x a pprox 0.}
Коэффициенты для серий синуса и косинуса, следовательно, могут быть получены путем подстановки их разложений в тождества пифагора и двойного угла, принимая ведущий коэффициент для синуса равным 1 и согласовывая остальные коэффициенты.
В общем, математически важные отношения между функциями синуса и косинуса и экспоненциальной функцией (см., Например, формулу Эйлера ) существенно упрощаются, когда углы выражаются в радианах, а не в градусах, градусах или других единицах. Поэтому в большинстве разделов математики, выходящих за рамки практической геометрии, считается, что углы выражаются в радианах.
Аналогичный ряд — это ряд Грегори для arctan, который получается путем опускания факториалов в знаменателе.
Непрерывная дробь
Функция синуса также может быть представлена как обобщенная непрерывная дробь :
- sin (x) = x 1 + x 2 2 ⋅ 3 — x 2 + 2 ⋅ 3 x 2 4 ⋅ 5 — x 2 + 4 ⋅ 5 x 2 6 ⋅ 7 — x 2 + ⋱. { displaystyle sin (x) = { cfrac {x} {1 + { cfrac {x ^ {2}} {2 cdot 3-x ^ {2} + { cfrac {2 cdot 3x ^ { 2}} {4 cdot 5-x ^ {2} + { cfrac {4 cdot 5x ^ {2}} {6 cdot 7-x ^ {2} + ddots}}}}}}}}.}
Представление непрерывной дроби может быть получено из формулы непрерывной дроби Эйлера и выражает вещественное число, как рациональное, так и иррациональное синусоидальной функции.
Фиксированная точка
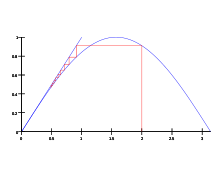
Ноль — единственная действительная фиксированная точка синусоидальной функции; другими словами, единственное пересечение синусоидальной функции и тождественной функции — это sin (0) = 0.
Длина дуги
Длина дуги синусоидальной кривой между a { displaystyle a}


Длина дуги для полного периода равна 4 2 π 3 Γ (1/4) 2 + Γ (1/4) 2 2 π = 7.640395578 … { Textstyle { frac {4 { sqrt {2 pi ^ {3}}}} { Gamma (1/4) ^ {2}}} + { frac { Gamma (1/4) ^ {2}} { sqrt {2 pi}}} = 7.640395578 ldots}

Длина дуги синусоидальной кривой от 0 до x равна приведенному выше числу, деленному на 2 π { displaystyle 2 pi}

- 1,21600672 x + 0,10317093 sin (2 x) — 0,00220445 sin (4 x) + 0,00012584 sin (6 x) — 0,00001011 sin (8 x) + ⋯ { displaystyle 1.21600672x + 0.10317093 sin (2x) -0.00220445 sin (4x) +0.00012584 sin (6x) -0.00001011 sin (8x) + cdots}
Главный член в приведенном выше уравнении и предел отношение длины дуги к расстоянию определяется следующим образом:
- π 2 + 2 Γ (3 4) 4 2 π 3/2 Γ (3 4) 2 { displaystyle { frac { pi ^ {2} +2 Гамма left ({ frac {3} {4}} right) ^ {4}} {{ sqrt {2}} pi ^ {3/2} Gamma left ({ frac {3} { 4}} right) ^ {2}}}}
Закон синусов
Закон синусов гласит, что для произвольного треугольника со сторонами a, b и c и углы, противоположные этим сторонам A, B и C:
- sin A a = sin B b = sin C c. { displaystyle { frac { sin A} {a}} = { frac { sin B} {b}} = { frac { sin C} {c}}.}
Это эквивалентно равенство первых трех выражений ниже:
- a sin sin A = b sin B = c sin C = 2 R, { displaystyle { frac {a} { sin A}} = { frac { b} { sin B}} = { frac {c} { sin C}} = 2R,}
где R — описанный радиус треугольника.
Это можно доказать, разделив треугольник на два правильные и используя приведенное выше определение синуса. Закон синусов полезен для вычисления длин неизвестных сторон треугольника, если известны два угла и одна сторона. Это обычная ситуация, возникающая в триангуляции, методе определения неизвестных расстояний путем измерения двух углов и доступного замкнутого расстояния.
Особые значения

Для некоторых целых чисел x градусов, значение sin (x) особенно просто. Таблица некоторых из этих значений приведена ниже.
| x (угол) | sin (x) | ||||
|---|---|---|---|---|---|
| Градусы | Радианы | Градианы | Повороты | Точное значение | Десятичное число |
| 0° | 0 | 0 | 0 | 0 | 0 |
| 180 ° | π | 200 | 1/2 | ||
| 15 ° | 1 / 12π | 16+2/3 | 1/24 | 6 — 2 4 { displaystyle { frac {{ sqrt {6}} — { sqrt {2}}} {4}}} |
0,258819045102521 |
| 165 ° | 11 / 12π | 183 + 1/3 | 11/24 | ||
| 30 ° | 1 / 6π | 33+1/3 | 1/12 | 1/2 | 0,5 |
| 150 ° | 5 / 6π | 166+2/3 | 5/12 | ||
| 45 ° | 1 / 4π | 50 | 1/8 | 2 2 { displaystyle { frac { sqrt {2}} {2}}} |
0,707106781186548 |
| 135 ° | 3 / 4π | 150 | 3/8 | ||
| 60 ° | 1 / 3π | 66 + 2/3 | 1/6 | 3 2 { displaystyle { frac { sqrt {3}} {2}}} |
0,866025403784439 |
| 120 ° | 2 / 3π | 133+1/3 | 1/3 | ||
| 75 ° | 5 / 12π | 83 + 1/3 | 5/24 | 6 + 2 4 { displaystyle { frac {{ sqrt {6}} + { sqrt {2}}} {4}}} |
0,965925826289068 |
| 105 ° | 7 / 12π | 116 + 2/3 | 7/24 | ||
| 90 ° | 1 / 2π | 100 | 1/4 | 1 | 1 |
с шагом 90 градусов:
| x в градусах | 0° | 90 ° | 180 ° | 270 ° | 360 ° |
| x в радианах | 0 | π / 2 | π | 3π / 2 | 2π |
| x в углах | 0 | 100 | 200 | 300 | 400 |
| x по очереди | 0 | 1/4 | 1/2 | 3/4 | 1 |
| sin x | 0 | 1 | 0 | -1 | 0 |
Другие значения, не указанные выше:
- sin (π 60) знак равно грех (3 ∘) знак равно (2–12) 5 + 5 + (10–2) (3 + 1) 16 { displaystyle sin left ({ frac { pi} {60}} right) = sin (3 ^ { circ}) = { frac {(2 — { sqrt {12}}) { sqrt {5 + { sqrt {5}}}} + ({ sqrt {10} } — { sqrt {2}}) ({ sqrt {3}} + 1)} {16}}}
OEIS : A019812
- грех (π 30) = грех (6 ∘) = 30 — 180 — 5 — 1 8 { displaystyle sin left ({ frac { pi} {30}} right) = sin (6 ^ { circ}) = { frac {{ sqrt {30 — { sqrt {180}}}} — { sqrt {5}} — 1} {8}}}
OEIS : A019815
- грех (π 20) знак равно грех (9 ∘) = 10 + 2-20-80 8 { displaystyle sin left ({ frac { pi} {20}} right) = sin (9 ^ { circ}) = { frac {{ sqrt {10}} + { sqrt {2}} — { sqrt {20 — { sqrt {80}}}}} {8}}}
OEIS : A019818
- грех (π 15) = грех (12 ∘) = 10 + 20 + 3-15 8 { displaystyle sin left ({ frac { pi} {15}} right) = sin (12 ^ { circ}) = { frac {{ sqrt {10 + { sqrt {20}}}} + { sqrt {3}} — { sqrt {15}}} {8}}}
OEIS : A019821
- грех (π 10) = грех (18 ∘) = 5 — 1 4 = 1 2 φ — 1 { displaystyle sin left ({ frac { pi} {10}} right) = sin (18 ^ { circ}) = { frac {{ sqrt {5}} — 1} {4}} = { tfrac {1} {2}} varphi ^ {- 1}}
OEIS : A019827
- sin (7 π 60) = sin (21 ∘) = (2 + 12) 5-5 — (10 + 2) (3-1) 16 { displaystyle sin left ({ frac {7 pi} {60}} right) = sin (21 ^ { circ}) = { frac {(2+ { sqrt {12}}) { sqrt {5 — { sqrt {5}}}} — ({ sqrt {10}} + { sqrt {2}}) ({ sqrt {3}} — 1)} {16}}}
OEIS : A019830
- грех (π
= грех (22,5 ∘) = 2–2 2 { displaystyle sin left ({ frac { pi} {8}} right) = sin (22,5 ^ { circ}) = { frac { sqrt {2 — { sqrt {2}}}} {2}}}
- грех (2 π 15) = грех (24 ∘) = 3 + 15 — 10 — 20 8 { displaystyle sin left ({ frac {2 pi} {15}} right) = sin (24 ^ { circ}) = { frac {{ sqrt { 3}} + { sqrt {15}} — { sqrt {10 — { sqrt {20}}}}} {8}}}
OEIS : A019833
- грех (3 π 20) знак равно грех (27 ∘) = 20 + 80-10 + 2 8 { displaystyle sin left ({ frac {3 pi} {20}} right) = sin (27 ^ { circ}) = { frac {{ sqrt {20 + { sqrt {80}}}} — { sqrt {10}} + { sqrt {2}}} {8}}}
OEIS : A019836
- грех (11 π 60) = грех (33 ∘) = (12–2) 5 + 5 + (10–2) (3 + 1) 16 { displaystyle sin left ({ frac {11 pi} {60}} right) = sin (33 ^ { circ}) = { frac {({ sqrt {12}} — 2) { sqrt {5 + { sqrt {5}}}} + ({ sqrt {10}} — { sqrt {2}}) ({ sqrt {3}} + 1)} {16}}}
OEIS : A019842
- грех (π 5) = грех (36 ∘) = 10-20 4 { displaystyle sin left ({ frac { pi} {5}} справа) = sin (36 ^ { circ}) = { frac { sqrt {10 — { sqrt {20}}}} {4}}}
OEIS : A019845
- грех (13 π 60) = грех (39 ∘) = (2–12) 5–5 + (10 + 2) (3 + 1) 16 { displaystyle sin left ({ frac {13 число Пи } {60}} right) = sin (39 ^ { circ}) = { frac {(2 — { sqrt {12}}) { sqrt {5 — { sqrt {5}}}} + ({ sqrt {10}} + { sqrt {2}}) ({ sqrt {3}} + 1)} {16}}}
OEIS : A019848
- грех (7 π 30) знак равно грех (42 ∘) = 30 + 180 — 5 + 1 8 { displaystyle sin left ({ frac {7 pi} {30}} right) = sin ( 42 ^ { circ}) = { frac {{ sqrt {30 + { sqrt {180}}}} — { sqrt {5}} + 1} {8}}}
OEIS : A019851
Связь с комплексными числами

Синус используется для определения мнимой части комплексного числа , заданного в полярных координатах. (г, φ):
- Z знак равно р (соз (φ) + я грех (φ)) { Displaystyle Z = г ( соз ( varphi) + я грех ( varphi))}
мнимая часть:
- Im (z) = r sin (φ) { displaystyle operatorname {Im} (z) = r sin ( varphi)}
r и φ представляют собой величину и угол комплексного числа соответственно. i — это мнимая единица. z — комплексное число ..
Несмотря на то, что мы имеем дело с комплексными числами, параметр синуса в этом случае по-прежнему является действительным числом. Синус также может принимать в качестве аргумента комплексное число.
Синус с комплексным аргументом
sin (z) { displaystyle sin (z)}


sin (θ) { displaystyle sin ( theta)}

ei θ { displaystyle e ^ {i theta}}

Определение синусоидальной функции для комплексных аргументов z:
- sin (z) = ∑ n = 0 ∞ (- 1) n ( 2 п + 1)! z 2 N + 1 знак равно eiz — е — iz 2 i = sinh (iz) i { displaystyle { begin {align} sin (z) = sum _ {n = 0} ^ { infty} { frac {(-1) ^ {n}} {(2n + 1)!}} z ^ {2n + 1} \ = { frac {e ^ {iz} -e ^ {- iz}} { 2i}} \ = { frac { sinh left (iz right)} {i}} end {align}}}
где i = −1, а sinh — гиперболический синус. Это целая функция. Кроме того, для чисто вещественного x
- sin (x) = Im (e i x). { displaystyle sin (x) = operatorname {Im} (e ^ {ix}).}
Для чисто мнимых чисел:
- sin (i y) = i sinh (y). { displaystyle sin (iy) = i sinh (y).}
Также иногда полезно выразить сложную синусоидальную функцию в терминах действительной и мнимой частей ее аргумента:
- sin (x + iy) = sin (x) cos (iy) + cos (x) sin (iy) = sin (x) cosh (y) + i cos (x) sinh (y). { Displaystyle { begin {align} sin (x + iy) = sin (x) cos (iy) + cos (x) sin (iy) \ = sin (x) cosh (y) + i cos (x) sinh (y). end {align}}}
Разложение на частичную дробь и произведение комплексного синуса
Использование техники разложения на частичную дробь в комплексный анализ, можно найти, что бесконечный ряд
- ∑ n = — ∞ ∞ (- 1) nz — n = 1 z — 2 z ∑ n = 1 ∞ (- 1) nn 2 — z 2 { displaystyle { begin {align} sum _ {n = — infty} ^ { infty} { frac {(-1) ^ {n}} {zn}} = { frac {1} {z} } -2z sum _ {n = 1} ^ { infty} { frac {(-1) ^ {n}} {n ^ {2} -z ^ {2}}} end {выровнено}}}
сходятся и равны π sin (π z) { textstyle { frac { pi} { sin ( pi z)}}}
- π 2 sin 2 (π z) = ∑ n = — ∞ ∞ 1 (z — n) 2. { displaystyle { begin {align} { frac { pi ^ {2}} { sin ^ {2} ( pi z)}} = sum _ {n = — infty} ^ { infty} { frac {1} {(zn) ^ {2}}}. end {align}}}
Используя технику расширения произведения, можно вывести
- sin (π z) = π z ∏ n = 1 ∞ (1 — z 2 n 2). { displaystyle { begin {align} sin ( pi z) = pi z prod _ {n = 1} ^ { infty} left (1 — { frac {z ^ {2}} {n ^{2}}}right).end{aligned}}}
Alternatively, the infinite product for the sine can be proved using complex Fourier series.
| Proof of the infinite product for the sine |
|---|
|
Using complex Fourier series, the function cos ( zx) {displaystyle cos(zx)}
Setting x = π {displaystyle x=pi }
Therefore we get
The function π cot ( π z) {displaystyle pi cot(pi z)}
Exponentiating gives
Since lim z → 0 sin ( π z) z = π {textstyle lim _{zto 0}{frac {sin(pi z)}{z}}=pi }
for some open and connected subset of C {displaystyle mathbb {C} } |
Usage of complex sine
sin(z) is found in the functional equation for the Gamma function,
- Γ ( s) Γ ( 1 − s) = π sin ( π s), {displaystyle Gamma (s)Gamma (1-s)={pi over sin(pi s)},}
which in turn is found in the functional equation for the Riemann zeta-function,
- ζ ( s) = 2 ( 2 π) s − 1 Γ ( 1 − s) sin ( π s / 2) ζ ( 1 − s). {displaystyle zeta (s)=2(2pi)^{s-1}Gamma (1-s)sin(pi s/2)zeta (1-s).}
As a holomorphic function, sin z is a 2D solution of Laplace’s equation :
- Δ u ( x 1, x 2) = 0. {displaystyle Delta u(x_{1},x_{2})=0.}
The complex sine function is also related to the level curves of pendulums.
Complex graphs
 |
 |
 |
| real component | imaginary component | magnitude |
.
 |
 |
 |
| real component | imaginary component | magnitude |
History
While the early study of trigonometry can be traced to antiquity, the trigonometric functions as they are in use today were developed in the medieval period. The chord function was discovered by Hipparchus of Nicaea (180–125 BCE) and Ptolemy of Rom Египет (90–165 гг. н. э.).
Функцию синуса и версин (1 — косинус) можно проследить до функций jyā и koṭi-jyā, используемых в период Гупты (320–550 гг. Н. Э.) Индийская астрономия (Арьябхатия, Сурья Сиддханта ) посредством перевода с санскрита на арабский, а затем с арабского на латинский.
Все шесть используемых в настоящее время тригонометрических функций были известны в исламской математике к 9 веку, как и закон синусов, использовавшийся в решении треугольников. За исключением синуса (который был заимствован из индийской математики), арабскими математиками были открыты другие пять современных тригонометрических функций, включая косинус, тангенс, котангенс, секанс и косеканс. Аль-Хваризми (ок. 780–850) составил таблицы синусов, косинусов и тангенсов. Мухаммад ибн Джабир аль-Харрани аль-Баттани (853–929) открыл взаимные функции секанса и косеканса и создал первую таблицу косекансов. для каждой степени от 1 ° до 90 °.
Первое опубликованное использование сокращений sin, cos и tan принадлежит французскому математику 16 века Альбер Жирар ; в дальнейшем они были обнародованы Эйлером (см. ниже). Opus palatinum de triangulis Георга Иоахима Ретикуса, ученика Коперника, вероятно, был первым в Европе, который определил тригонометрические функции непосредственно в терминах прямоугольных треугольников, а не окружностей, с таблицами для все шесть тригонометрических функций; эта работа была закончена учеником Ретикуса Валентином Отоном в 1596 году.
В статье, опубликованной в 1682 году, Лейбниц доказал, что sin x не является алгебраической функцией x Роджер Котес вычислил производную синуса в своей Harmonia Mensurarum (1722). Введение Леонарда Эйлера в анализ бесконечности (1748) в основном отвечало за установление аналитического подхода к тригонометрическим функциям. в Европе, также определяя их как бесконечные серии и представляя «формулу Эйлера », а также почти современные сокращения sin., cos., tang., cot., sec. и cosec.
Этимология
| Найдите sine в Wiktionary, бесплатном словаре. |
Этимологически слово синус происходит от санскрита слово, обозначающее аккорд, jiva * (jya — его более популярный синоним). Это было транслитерировано на арабском как jiba جيب, что, однако, не имеет смысла на этом языке и сокращается как jb جب. Поскольку арабский язык написан без коротких гласных, «jb» интерпретировалось как слово jaib جيب, что означает «грудь». Когда в XII веке арабские тексты были переведены на латинский Герардом Кремонским, он использовал латинский эквивалент слова «лоно», sinus (что означает « лоно »или« гнедой »или« складкой »). Джерард, вероятно, был не первым ученым, использовавшим этот перевод; Роберт Честерский, кажется, предшествовал ему, и есть свидетельства более раннего использования. Английская форма синуса была введена в 1590-х годах.
Программные реализации
Не существует стандартного алгоритма для вычисления синуса. IEEE 754-2008, наиболее широко используемый стандарт для вычислений с плавающей запятой, не касается вычисления тригонометрических функций, таких как синус. Алгоритмы вычисления синуса могут быть сбалансированы с учетом таких ограничений, как скорость, точность, переносимость или диапазон принимаемых входных значений. Это может привести к разным результатам для разных алгоритмов, особенно для особых обстоятельств, таких как очень большие входные данные, например sin (10).
Некогда распространенная оптимизация программирования, особенно используемая в трехмерной графике, заключалась в предварительном вычислении таблицы значений синуса, например, одно значение на градус. Это позволяло искать результаты в таблице, а не рассчитывать их в реальном времени. С современной архитектурой ЦП этот метод не может дать никаких преимуществ.
Алгоритм CORDIC обычно используется в научных калькуляторах.
Функция синуса, наряду с другими тригонометрическими функциями, широко доступна для разных языков и платформ программирования. В вычислениях это обычно сокращается до sin.
Некоторые архитектуры ЦП имеют встроенную инструкцию для синуса, включая FPU Intel x87 начиная с 80387.
В языках программирования sinобычно либо встроенная функция, либо находится в стандартной математической библиотеке языка.
Например, стандартная библиотека C определяет синусоидальные функции в пределах math.h : sin (double ), sinf (float )и sinl (long double ). Параметром каждого из них является значение с плавающей запятой, определяющее угол в радианах. Каждая функция возвращает тот же тип данных , который принимает.Множество других тригонометрических функций также определены в math.h, например, для косинуса, арксинуса и гиперболического синуса (sinh).
Аналогично, Python определяет math.sin (x)во встроенном модуле math. Сложные синусоидальные функции также доступны в Модуль cmath, например, cmath.sin (z). Математические функции CPython вызывают библиотеку C mathи используют Формат с плавающей запятой двойной точности.
.
Реализации на основе поворотов
Некоторые программные библиотеки предоставляют реализации синусоиды с использованием входного угла в половину- оборотов, где пол-оборота составляет угол 180 градусы или π { displaystyle pi}
| Окружение | Название функции | Угловые единицы |
|---|---|---|
| MATLAB | sinpi |
полуобороты |
| OpenCL | sinpi |
полуобороты |
| R | sinpi |
полуобороты |
| Julia | sinpi |
полуобороты |
| CUDA | sinpi |
полуобороты |
| ARM | sinpi |
полуобороты |
Преимущество точности проистекает из способности идеально представлять ключевые углы, такие как полный оборот, полуоборот и четверть оборота, без потерь в двоичной системе с плавающей запятой или с фиксированной запятой. Напротив, представляя 2 π { displaystyle 2 pi}


Повороты также имеют преимущество в точности и эффективности для вычисления по модулю до одного периода. Вычисление по модулю 1 оборот или по модулю 2 полуоборотов может выполняться без потерь и эффективно как с плавающей, так и с фиксированной точкой. Например, вычисление по модулю 1 или 2 для значения с фиксированной запятой, масштабированного по двоичной точке, требует только битового сдвига или операции побитового И. Напротив, вычисление по модулю π 2 { displaystyle { frac { pi} {2}}}

Для приложений, связанных с датчиками угла, датчик обычно обеспечивает угловые измерения в форме, напрямую совместимой с поворотами или полуоборотами. Например, датчик угла может отсчитывать от 0 до 4096 за один полный оборот. Если полуворота используются в качестве единицы измерения угла, тогда значение, предоставляемое датчиком, напрямую и без потерь отображается в тип данных с фиксированной точкой с 11 битами справа от двоичной точки. Напротив, если радианы используются в качестве единицы для хранения угла, то неточности и стоимость умножения необработанного целого числа датчика на приближение к π 2048 { displaystyle { frac { pi} {2048}}}
См. Также
- таблицу синусов Рьябханы
- Формула аппроксимации синуса Бхаскары I
- Дискретное синусоидальное преобразование
- Формула Эйлера
- Обобщенная тригонометрия
- Гиперболическая функция
- Закон синусов
- Список периодических функций
- Список тригонометрических тождеств
- Серия Мадхав
- Таблица синусов Мадхавы
- Теорема оптического синуса
- Полярный синус — обобщение на углы вершин
- Доказательства тригонометрических тождества
- функция Sinc
- преобразования синуса и косинуса
- интеграл синуса
- квадрант синуса
- волна синуса
- уравнение синуса – Гордона
- синусоидальная модель
- тригонометрические функции
- тригонометрический интеграл
Цитаты
Ссылки
- Траупман, доктор философии, Джон К. (1966), Латинский и английский словарь Нью-колледжа, Торонто: Bantam, ISBN 0-553-27619-0
- Седьмой новый университетский словарь Вебстера, Спрингфилд: G. C. Merriam Company, 1969
Внешние ссылки
СМИ, связанные с функцией синуса на Wikimedia Commons
| Найдите sine в Wiktionary, бесплатном словаре. |
Тригонометрия — раздел математической науки, в котором изучаются тригонометрические функции и их использование в геометрии. Развитие тригонометрии началось еще во времена античной Греции. Во времена средневековья важный вклад в развитие этой нужной науки внесли ученые Ближнего Востока и Индии, которые придумали наиболее важные понятия, объяснили многие свойства, предложили варианты измерения и др.
Данная статья посвящена базовым понятиям и дефинициям тригонометрии. В ней рассмотрены определения основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Разъяснен и проиллюстрирован их смысл в контексте геометрии без таблиц и графиков.
Синус, косинус, тангенс и котангенс. Определения
Зачем разделять понятия синуса, косинуса, тангенса и котангенса?
Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.
Что такое синус?
Синус угла (sin α) — это отношение противолежащего этому углу катета к гипотенузе.
Что такое косинус?
Косинус угла (cosα) — это отношение прилежащего катета к гипотенузе.
Что такое тангенс?
Тангенс угла (tg α) — это отношение противолежащего катета к прилежащему.
Котангенс угла (ctg α) — отношение прилежащего катета к противолежащему.
Данные определения даны для острого угла прямоугольного треугольника!
Синус и косинус можно представить через экспоненту (экспоненциальная функция).
Приведем иллюстрацию.
В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.
Означения синуса, косинуса, тангенса и котангенса позволяют вычислять (находить) значения этих функций по известным длинам сторон треугольника.
Что и почему важно и принято помнить в ходе такого нахождения?
Область значений синуса и косинуса: от -1 до 1. Иными словами синус и косинус принимают значения от -1 до 1. Область значений тг и ктг — вся числовая прямая, то есть эти функции могут принимать любые значения.
Как найти синус? Для начала нужно определиться, какой перед нами треугольник: прямоугольный или произвольный. В первом случае можно использовать обычный тригонометрический метод, а во втором — теорему косинусов.
Как найти косинус? Соответственно, нам нужно знать значения прилежающего катета и гипотенузы.
Как найти тангенс? Если треугольник прямоугольный, то тангенс вычисляется при помощи значений противоположного катета и прилежащего (в уравнении нужно поделить одно на другое). Если речь идет о числах, тупых, развернутых углов и углов, превышающих 360 градусов, то тангенс определяется при помощи синуса и косинуса (посредством их отношения и деления).
Теорема синусов и косинусов используется для того чтобы искать элементы в произвольном треугольнике. Такой поиск используется часто.
Угол поворота
Определения, данные выше, относятся к острым углам. В тригонометрии вводится понятие угла поворота, величина которого, в отличие от острого угла, не ограничена рамками от 0 до 90 градусов.Угол поворота в градусах или радианах выражается любым действительным числом от -∞ до +∞.
В данном контексте можно дать определение синуса, косинуса, тангенса и котангенса угла произвольной величины. Представим единичную окружность (круг) с центром в начале декартовой системы координат.
Начальная точка A с координатами (1, 0) поворачивается вокруг центра единичной окружности на некоторый угол α и переходит в точку A1. Определение дается через координаты точки A1(x , y).
Синус угла поворота α — это ордината точки A1(x , y). sin α=y
Косинус угла поворота α — это абсцисса точки A1(x , y). cos α=икс
Тангенс угла поворота α — это отношение ординаты точки A1(x , y) к ее абсциссе. tg α=yx
Котанг угла поворота α — это отношение абсциссы точки A1(x , y) к ее ординате. ctg α=xy
Синус и косинус определены для любого угла поворота. Это логично, ведь абсциссу и ординату точки после поворота можно определить при любом угле. Иначе обстоит дело с тангенсом и котангенсом. Тангенс не определен, когда точка после поворота переходит в точку с нулевой абсциссой (0, 1) и (0, -1). В таких случаях выражение для тангенса tg α=yx просто не имеет смысла, так как в нем присутствует деление на ноль. Аналогична ситуация с котангенсом. Отличие состоит в том, что котангенс не определен в тех случаях, когда в ноль обращается ордината точки.
Простое правило: синус и косинус определены для любых углов α.
Тангенс определен для всех углов, кроме α=90°+180°·k, k∈Z (α=π2+π·k, k∈Z)
Котангенс определен для всех углов, кроме α=180°·k, k∈Z (α=π·k, k∈Z)
При решении практических примеров не говорят «синус угла поворота α». Слова «угол поворота» просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь.
Числа
Как быть с определением синуса, косинуса, тангенса и котангенса числа, а не угла поворота?
Синусом, косинусом, тангенсом и котангенсом числа t называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в t радиан.
Например, синус числа 10π равен синусу угла поворота величиной 10π рад.
Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Рассмотрим его подробнее.
Любому действительному числу t ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат. Синус, косинус, тангенс и котангенс определяются через координаты этой точки.
Начальная точка на окружности — точка A c координатами (1, 0).
Положительному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t.
Отрицательному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t.
Теперь, когда связь числа и точки на окружности установлена, переходим к определению синуса, косинуса, тангенса и котангенса.
Синус числа t — ордината точки единичной окружности, соответствующей числу t. sin t=y
Косинус числа t — абсцисса точки единичной окружности, соответствующей числу t. cos t=x
Тангенс числа t — отношение ординаты к абсциссе точки единичной окружности, соответствующей числу t. tg t=yx=sin tcos t
Последние определения находятся в соответствии и не противоречат определению, данному в начале это пункта. Точка на окружности, соответствующая числу t, совпадает с точкой, в которую переходит начальная точка после поворота на угол t радиан.
Тригонометрические функции углового и числового аргумента
Каждому значению угла α соответствует определенное значение синуса и косинуса этого угла. Также, как всем углам α, отличным от α = 90 ° + 180 ° · k , k ∈ Z ( α = π 2 + π · k , k ∈ Z ) соответствует определенное значение тангенса. Котангенс, как сказано выше, определен для всех α, кроме α = 180 ° · k , k ∈ Z ( α = π · k , k ∈ Z ).
Можно сказать, что sin α, cos α, tg α, ctg α — это функции угла альфа, или функции углового аргумента.
Аналогично можно говорить о синусе, косинусе, тангенсе и котангенсе, как о функциях числового аргумента. Каждому действительному числу t соответствует определенное значение синуса или косинуса числа t. Всем числам, отличным от π 2 + π · k , k ∈ Z соответствует значение тангенса. Котангенс, аналогично, определен для всех чисел, кроме π · k , k ∈ Z.
Синус, косинус, тангенс и котангенс — основные тригонометрические функции.
Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело.
Связь определений sin, cos, tg и ctg из геометрии и тригонометрии
Вернемся к данным в самом начале определениям и углу альфа, лежащему в пределах от 0 до 90 градусов. Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью соотношений сторон прямоугольного треугольника. Покажем это.
Возьмем единичную окружность с центром в прямоугольной декартовой системе координат. Повернем начальную точку A(1,0) на угол величиной до 90 градусов и проведем из полученной точки A1(x,y) перпендикуляр к оси абсцисс. В полученном прямоугольном треугольнике угол A1OH равен углу поворота α, длина катета OH равна абсциссе точки A1(x,y). Длина катета, противолежащего углу, равна ординате точки A1(x,y), а длина гипотенузы равна единице, так как она является радиусом единичной окружности.
В соответствии с определением из геометрии, синус угла α равен отношению противолежащего катета к гипотенузе.
sin α=A1HOA1=y1=y
Значит, определение синуса острого угла в прямоугольном треугольнике через соотношение сторон эквивалентно определению синуса угла поворота α, при альфа лежащем в пределах от 0 до 90 градусов.
Аналогично соответствие определений можно показать для косинуса, тангенса и котангенса.
Синус, косинус, тангенс и котангенс: основные формулы
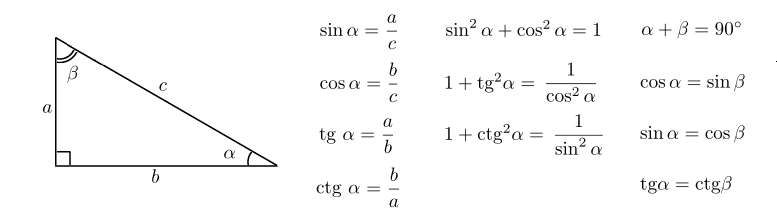
Для удобства сразу же приведем таблицу с всеми тригонометрическими тождествами. Всегда удобно открыть формулы в одном месте, выбрать нужную и решить пример. После таблицы мы по отдельности рассмотрим каждую тригонометрическую формулу: обсудим ее вывод и порешаем примеры.
- Основное тригонометрическое тождество:
$$sin(alpha)^2+cos(alpha)^2=1;$$ - Определение тангенса и котангенса через синус и косинус:
$$tg(alpha)=frac{sin(alpha)}{cos(alpha)};$$
$$ctg(alpha)=frac{cos(alpha)}{sin(alpha)};$$ - Cвязь тангенса и котангенса:
$$tg(alpha)=frac{1}{ctg(alpha)};$$
$$tg(alpha)*ctg(alpha)=1;$$ - Тангенс через косинус. Котангенс через синус:
$$tg(alpha)^2+1=frac{1}{cos(alpha)^2};$$
$$ctg(alpha)^2+1=frac{1}{sin(alpha)^2};$$ - Синус суммы и разности:
$$sin(alpha+beta)=sin(alpha)*cos(beta)+sin(beta)*cos(alpha);$$
$$sin(alpha-beta)=sin(alpha)*cos(beta)-sin(beta)*cos(alpha);$$ - Косинус суммы и разности:
$$cos(alpha+beta)=cos(alpha)*cos(beta)-sin(beta)*sin(alpha);$$
$$cos(alpha-beta)=cos(alpha)*cos(beta)+sin(beta)*sin(alpha);$$ - Тангенс суммы и разности:
$$tg(alpha+beta)=frac{tg(alpha)+tg(beta)}{1-tg(alpha)*tg(beta)};$$
$$tg(alpha-beta)=frac{tg(alpha)-tg(beta)}{1+tg(alpha)*tg(beta)};$$ - Котангенс суммы и разности:
$$сtg(alpha+beta)=frac{-1+сtg(alpha)*ctg(beta)}{ctg(alpha)+ctg(beta)};$$
$$сtg(alpha-beta)=frac{-1-сtg(alpha)*ctg(beta)}{ctg(alpha)-ctg(beta)};$$ - Двойной угол:
$$cos(2*alpha)=cos(alpha)^2-sin(alpha)^2=1-2*sin(alpha)^2=2*cos(alpha)^2-1;$$
$$sin(2*alpha)=2*sin(alpha)*cos(alpha);$$
$$tg(2*alpha)=frac{2*tg(alpha)}{1-tg(alpha)^2};$$
$$ctg(2*alpha)=frac{ctg(alpha)^2-1}{2*ctg(alpha)};$$ - Тройной угол:
$$cos(3*alpha)=cos(alpha)^3-3*sin(alpha)^2*cos(alpha)=-3*cos(alpha)+4*cos(alpha)^3;$$
$$sin(3*alpha)=3*sin(alpha)*cos(alpha)^2-sin(alpha)^3=3*sin(alpha)-4*sin(alpha)^3;$$
$$tg(3*alpha)=frac{3*tg(alpha)-tg(alpha)^3}{1-3*tg(alpha)^2};$$
$$ctg(3*alpha)=frac{ctg(alpha)^3-3*ctg(alpha)}{3*ctg(alpha)^2-1};$$ - Формулы половинного угла:
$$sin(frac{alpha}{2})^2=frac{1-cos(alpha)}{2};$$
$$cos(frac{alpha}{2})^2=frac{1+cos(alpha)}{2};$$
$$tg(frac{alpha}{2})^2=frac{1-cos(alpha)}{1+cos(alpha)};$$
$$ctg(frac{alpha}{2})^2=frac{1+cos(alpha)}{1-cos(alpha)};$$ - Понижение степени:
$$sin(alpha)^2=frac{1-cos(2*alpha)}{2};$$
$$cos(alpha)^2=frac{1+cos(2*alpha)}{2};$$
$$sin(alpha)^3=frac{3*sin(alpha)-sin(3*alpha)}{4};$$
$$cos(alpha)^3=frac{3*cos(alpha)+cos(3*alpha)}{4};$$
$$sin(alpha)^4=frac{3-4*cos(2*alpha)+cos(4*alpha)}{8};$$
$$cos(alpha)^4=frac{3+4*cos(2*alpha)+cos(4*alpha)}{8};$$ - Преобразование суммы и разности тригонометрических функций:
$$sin(alpha)+sin(beta)=2*sinleft(frac{alpha+beta}{2}right)*cosleft(frac{alpha-beta}{2}right);$$
$$sin(alpha)-sin(beta)=2*sinleft(frac{alpha-beta}{2}right)*cosleft(frac{alpha+beta}{2}right);$$
$$cos(alpha)+cos(beta)=2*cosleft(frac{alpha+beta}{2}right)*cosleft(frac{alpha-beta}{2}right);$$
$$cos(alpha)-cos(beta)=-2*sinleft(frac{alpha+beta}{2}right)*sinleft(frac{alpha-beta}{2}right);$$
$$cos(alpha)-cos(beta)=2*sinleft(frac{alpha+beta}{2}right)*sinleft(frac{beta-alpha}{2}right);$$
$$tg(alpha)+tg(beta)=frac{sin(alpha+beta)}{cos(alpha)*cos(beta)};$$
$$tg(alpha)-tg(beta)=frac{sin(alpha-beta)}{cos(alpha)*cos(beta)};$$
$$ctg(alpha)+ctg(beta)=frac{sin(alpha+beta)}{sin(alpha)*sin(beta)};$$
$$ctg(alpha)-ctg(beta)=frac{sin(beta-alpha)}{sin(alpha)*sin(beta)};$$ - Преобразование произведения тригонометрических функций:
$$sin(alpha)*sin(beta)=frac{1}{2}*left(cos(alpha-beta)-cos(alpha+beta)right);$$
$$cos(alpha)*cos(beta)=frac{1}{2}*left(cos(alpha-beta)+cos(alpha+beta)right);$$
$$sin(alpha)*cos(beta)=frac{1}{2}*left(sin(alpha-beta)+sin(alpha+beta)right);$$ - Формулы подстановки тангенса:
$$sin(alpha)=frac{2*tg(frac{alpha}{2})}{1+tg(frac{alpha}{2})^2};$$
$$cos(alpha)=frac{1-tg(frac{alpha}{2})^2}{1+tg(frac{alpha}{2})^2};$$
$$tg(alpha)=frac{2*tg(frac{alpha}{2})}{1-tg(frac{alpha}{2})^2};$$
$$ctg(alpha)=frac{1-tg(frac{alpha}{2})^2}{2*tg(frac{alpha}{2})};$$ - Формулы приведения можно найти в отдельной статье
Зачем нужны тригонометрические формулы?
Как видите, тригонометрических формул очень много. Тут еще и не все приведены. Но на ваше счастье, учить всю эту таблицу не нужно. Достаточно знать только основные: №1-6, 9. Остальные на ЕГЭ по профильной математике встречаются крайне редко, а если и попадутся, то, скорее всего, будут даны в справочных материалах.
Но для участия в олимпиадах или, если вы хотите поступать в сильный математический ВУЗ через вступительные экзамены, то вам может понадобиться вся таблица. По крайней мере, у вас точно должно быть представление о существовании таких формул, чтобы их вывести в случае необходимости. Да, большинство из них легко выводятся.
Тригонометрические формулы нужны, чтобы связать все тригонометрические функции между собой. Если вы знаете одну из функций, например, синус, то, используя эти формулы, можно легко найти оставшиеся три тригонометрические функции (косинус, тангенс и котангенс). Кроме этого тождества позволяют упростить выражение под тригонометрической функцией: например, выразить синус от двойного угла через комбинацию тригонометрических функций от одинарного угла, что бывает очень полезно при решении тригонометрических уравнений и неравенств.
Обсудим и порешаем примеры на все формулы из таблицы.
Основное тригонометрическое тождество
$$mathbf{sin(alpha)^2+cos(alpha)^2=1;}$$
Эту формулу можно считать главной и самой часто используемой в тригонометрии. Она выводится при помощи определения синуса и косинуса через прямоугольный треугольник и теоремы Пифагора. Не буду еще раз описывать вывод, с ним можно познакомиться в самой первой главе по тригонометрии.
При помощи основного тригонометрического тождества очень удобно искать значение синуса, если известен косинус и наоборот. Разберем пример:
Пример 1
Найдите (3sqrt{2}*sin(alpha)=?), если (cos(alpha)=frac{1}{3}) и (alphain(0;frac{pi}{2})). (ЕГЭ)
Чтобы найти значение выражения (3sqrt{2}*sin(alpha)) необходимо сначала найти значение синуса.
Формула, которая связывает и синус, и косинус — это основное тригонометрическое тождество:
$$sin(alpha)^2+cos(alpha)^2=1;$$
Просто подставим в нее известное значение косинуса
$$sin(alpha)^2+left(frac{1}{3}right)^2=1;$$
$$sin(alpha)^2+frac{1}{9}=1;$$
$$sin(alpha)^2=1-frac{1}{9};$$
$$sin(alpha)^2=frac{8}{9};$$
$$sin(alpha)=pmsqrt{frac{8}{9}}=pmfrac{2sqrt{2}}{3};$$
Обратите внимание на знак (pm), отрицательное значение синуса нас тоже устраивает, так как при подстановке и возведении в квадрат знак минус исчезает.
В задании указано, что это пример из ЕГЭ первой части, значит должен быть только один ответ. Какое же значение синуса нам выбрать: положительное или отрицательное?
В этом нам поможет дополнительное условие на (alphain(0;frac{pi}{2})), что соответсвует первой четверти на тригонометрической окружности. Раз (alpha) лежит в первой четверти, то синус должен быть положительный. Выбираем положительное значение синуса:
$$sin(alpha)=frac{2sqrt{2}}{3};$$
И подставим найденное значение в искомое выражение:
$$3sqrt{2}*sin(alpha)=3sqrt{2}*frac{2sqrt{2}}{3}=4.$$
Ответ: (4.)
Аналогично по основному тригонометрическому тождеству можно находить значение косинуса, если известен синус.
Основные тригонометрическое тождество это ключ к решению более половины всех тригонометрических уравнений.
Основные связи тригонометрических функций
А как найти тангенс или котангенс, если нам, например, известен косинус? Посмотрите на формулы №2, для того, чтобы найти тангенс, нужно знать и косинус, и синус:
$$mathbf{tg(alpha)=frac{sin(alpha)}{cos(alpha)};}$$
$$mathbf{ctg(alpha)=frac{cos(alpha)}{sin(alpha)};}$$
Но зная косинус, мы легко можем найти синус по основному тригонометрическому тождеству, а потом уже найти тангенс.
Пример 2
Найдите (tg(alpha)) и (ctg(alpha)), если (cos(alpha)=frac{sqrt{10}}{10}) и (alpha in (frac{3pi}{2};2pi)).
Сначала находим значение синуса:
$$sin(alpha)^2+cos(alpha)^2=1;$$
$$sin(alpha)^2+left(frac{sqrt{10}}{10}right)^2=1;$$
$$sin(alpha)^2+frac{1}{10}=1;$$
$$sin(alpha)^2=1-frac{1}{10};$$
$$sin(alpha)^2=frac{9}{10};$$
$$sin(alpha)=pmsqrt{frac{9}{10}}=pmfrac{3}{sqrt{10}};$$
Так как по условию задачи (alpha in (frac{3pi}{2};2pi)), что соответсвует четвертой четверти на тригонометрической окружности, то (sin(alpha)<0). Выбираем отрицательное значение:
$$sin(alpha)=-frac{3}{sqrt{10}};$$
Теперь нам известны значения и косинуса, и синуса, можем найти тангенс:
$$tg(alpha)=frac{sin(alpha)}{cos(alpha)}=frac{-frac{3}{sqrt{10}}}{frac{sqrt{10}}{10}}=-frac{3}{sqrt{10}}*frac{10}{sqrt{10}}=-3;$$
Котангенс можно найти аналогично по формуле:
$$ctg(alpha)=frac{cos(alpha)}{sin(alpha)};$$
Но поступим проще и воспользуемся тригонометрической формулой, связывающей тангенс с котангенсом:
$$mathbf{сtg(alpha)=frac{1}{tg(alpha)};}$$
$$сtg(alpha)=frac{1}{-3}=-frac{1}{3};$$
Ответ: (tg(alpha)=-3;) (ctg(alpha)=-frac{1}{3}.)
Как видите, чтобы найти тангенс или котангенс через косинус или синус, необходимо воспользоваться сразу двумя тригонометрическими формулами. Это не очень удобно, поэтому очень полезны тригонометрические формулы, связывающие тангенс с косинусом или котангенс с синусом напрямую:
$$mathbf{tg(alpha)^2+1=frac{1}{cos(alpha)^2};}$$
$$mathbf{ctg(alpha)^2+1=frac{1}{sin(alpha)^2};}$$
Вывод связи тангенса с косинусом и котангенса с синусом
Полезно знать, как они выводятся. Вывод, на самом деле, элементарный, с использованием основного тригонометрического тождества и определения тангенса через синус и косинус:
$$tg(alpha)^2+1=frac{1}{cos(alpha)^2};$$
$$left(frac{sin(alpha)}{cos(alpha)}right)^2+1=frac{1}{cos(alpha)^2};$$
Приводим левую часть к общему знаменателю:
$$frac{sin(alpha)^2}{cos(alpha)^2}+frac{cos(alpha)^2}{cos(alpha)^2}=frac{1}{cos(alpha)^2};$$
$$frac{sin(alpha)^2+cos(alpha)^2}{cos(alpha)^2}=frac{1}{cos(alpha)^2};$$
В числителе у нас получилось основное тригонометрическое тождество:
$$frac{1}{cos(alpha)^2}=frac{1}{cos(alpha)^2};$$
Получилось верное равенство — формула доказана. Аналогично доказывается формула для котангенса и синуса. (В качестве упражнения докажите ее сами).
Если решать пример №2 по этим формулам, то решение заметно сокращается:
$$tg(alpha)^2+1=frac{1}{left(frac{sqrt{10}}{10}right)^2};$$
$$tg(alpha)^2+1=10;$$
$$tg(alpha)^2=9;$$
$$tg(alpha)=pm3;$$
Так как (alpha in (frac{3pi}{2};2pi)), то тангенс будет отрицательным:
$$tg(alpha)=-3;$$
Формулы суммы и разности тригонометрических функций
- Синус суммы и разности:
$$mathbf{sin(alpha+beta)=sin(alpha)*cos(beta)+sin(beta)*cos(alpha);}$$
$$mathbf{sin(alpha-beta)=sin(alpha)*cos(beta)-sin(beta)*cos(alpha);}$$ - Косинус суммы и разности:
$$mathbf{cos(alpha+beta)=cos(alpha)*cos(beta)-sin(beta)*sin(alpha);}$$
$$mathbf{cos(alpha-beta)=cos(alpha)*cos(beta)+sin(beta)*sin(alpha);}$$ - Тангенс суммы и разности:
$$mathbf{tg(alpha+beta)=frac{tg(alpha)+tg(beta)}{1-tg(alpha)*tg(beta)};}$$
$$mathbf{tg(alpha-beta)=frac{tg(alpha)-tg(beta)}{1+tg(alpha)*tg(beta)};}$$ - Котангенс суммы и разности:
$$mathbf{сtg(alpha+beta)=frac{-1+сtg(alpha)*ctg(beta)}{ctg(alpha)+ctg(beta)};}$$
$$mathbf{сtg(alpha-beta)=frac{-1-сtg(alpha)*ctg(beta)}{ctg(alpha)-ctg(beta)};}$$
Формулы суммы разности тригонометрических функций попадаются в ЕГЭ по профильной математике в №12. В прошлые года эти формулы давались в справочные материалах и учить их было не обязательно. Тем не менее, я бы рекомендовал выучить хотя бы формулы суммы и разности для синуса и косинуса.
Это не очень удобно, но иногда формулы суммы разности используют для вывода формул приведения:
Пример 3
Упростить выражение (sin(frac{pi}{2}+alpha)).
Воспользуемся формулой синуса суммы:
$$sin(alpha+beta)=sin(alpha)*cos(beta)+sin(beta)*cos(alpha);$$
$$sin(frac{pi}{2}+alpha)=sin(frac{pi}{2})*cos(alpha)+sin(alpha)*cos(frac{pi}{2})=$$
$$=1*cos(alpha)+sin(alpha)*0=cos(alpha);$$
Формулы суммы разности так же полезны, когда нужно посчитать значение тригонометрических функций некоторых нестандартных углов:
Пример 4
Найдите значение (sin(15^o)=?)
(15^o) нестандартный угол, вы его не найдете в тригонометрической таблице углов. Представим (15^o) в виде разности стандартных углов (15^o=45^o-30^o). И воспользуемся формулой синуса разности:
$$sin(alpha-beta)=sin(alpha)*cos(beta)-sin(beta)*cos(alpha);$$
$$sin(15^o)=sin(45^o-30^o)=sin(45^o)*cos(30^o)-sin(30^o)*cos(45^o)=$$
$$=frac{sqrt{2}}{2}*frac{sqrt{3}}{2}-frac{1}{2}*frac{sqrt{2}}{2}=$$
$$=frac{sqrt{6}}{4}-frac{sqrt{2}}{4}=frac{sqrt{6}-sqrt{2}}{4};$$
Вот мы наши синус (15^o). Получилось такое иррациональное некрасивое выражение, так и оставляем.
Ответ: (sin(15^o)=frac{sqrt{6}-sqrt{2}}{4}.)
Пример 5
Найдите значение (cos(75^o)=?)
(75^o) можно представить в виде суммы стандартных углов (75^o=30^o+45^o). Здесь воспользуемся формулой косинуса суммы:
$$cos(alpha+beta)=cos(30^o)*cos(45^o)-sin(30^0)*sin(45^0)=$$
$$=frac{sqrt{3}}{2}*frac{sqrt{2}}{2}-frac{1}{2}*frac{sqrt{2}}{2}=$$
$$=frac{sqrt{6}}{4}-frac{sqrt{2}}{4}=frac{sqrt{6}-sqrt{2}}{4};$$
У нас получился опять отвратительный ответ, но внимательный читатель заметит, что ответ такой же, как в предыдущем примере, это значит, что (cos(75^o)=sin(15^o)). Такой же вывод можно было бы сделать исходя из формул приведения и знания тригонометрической окружности.
Ответ: (cos(75^o)=frac{sqrt{6}-sqrt{2}}{4}.)
Мы не будем выводить эти формулы — это не самое приятное занятие. Их проще выучить, а вывод вам вряд ли когда-либо пригодится. Но сами формулы суммы и разности служат основой для доказательства других тригонометрических формул.
Формулы двойного угла
$$cos(2*alpha)=cos(alpha)^2-sin(alpha)^2=1-2*sin(alpha)^2=2*cos(alpha)^2-1;$$
$$sin(2*alpha)=2*sin(alpha)*cos(alpha);$$
$$tg(2*alpha)=frac{2*tg(alpha)}{1-tg(alpha)^2};$$
$$ctg(2*alpha)=frac{ctg(alpha)^2-1}{2*ctg(alpha)};$$
Формулы двойного угла для синуса, косинуса, тангенса и котангенса дают возможность выразить двойной угол (2alpha) через (alpha). Формулы для синуса и косинуса очень часто встречаются на ЕГЭ. Их обязательно нужно знать. Все они легко выводятся из формул синуса и косинуса суммы (формулы №5 и №6) :
$$cos(2alpha)=cos(alpha+alpha)=cos(alpha)*cos(alpha)-sin(alpha)*sin(alpha)=cos(alpha)^2-sin(alpha)^2;$$
Воспользовавшись основным тригонометрическим тождеством можно преобразовать эту формулу:
$$cos(2alpha)=cos(alpha)^2-sin(alpha)^2=1-sin(alpha)^2-sin(alpha)^2=1-2sin(alpha)^2;$$
$$cos(2alpha)=cos(alpha)^2-sin(alpha)^2=cos(alpha)^2-(1-cos(alpha)^2)=2cos(alpha)^2-1;$$
Синус двойного угла выводится аналогичным образом только с использованием формулы синуса суммы:
$$sin(2alpha)=sin(alpha)*cos(alpha)+sin(alpha)*cos(alpha)=2sin(alpha)cos(alpha);$$
Для вывода формул двойного угла для тангенса нам понадобится представить тангенс в виде отношения синуса к косинуса по определению и только что выведенные формулы синуса и косинуса двойного угла:
$$tg(2alpha)=frac{sin(2alpha)}{cos(2alpha)}=frac{2sin(alpha)cos(alpha)}{cos(alpha)^2-sin(alpha)^2}=frac{frac{2sin(alpha)cos(alpha)}{cos(alpha)^2}}{frac{cos(alpha)^2-sin(alpha)^2}{cos(alpha)^2}}=frac{frac{2sin(alpha)}{cos(alpha)}}{1-frac{sin(alpha)^2}{cos(alpha)^2}}=frac{2tg(alpha)}{1-tg(alpha)^2};$$
Котангенс двойного угла выводится абсолютно также:
$$сtg(2alpha)=frac{cos(2alpha)}{sin(2alpha)}=frac{cos(alpha)^2-sin(alpha)^2}{2sin(alpha)cos(alpha)}=frac{frac{cos(alpha)^2-sin(alpha)^2}{sin(alpha)^2}}{frac{2sin(alpha)cos(alpha)}{sin(alpha)^2}}=frac{frac{cos(alpha)^2}{sin(alpha)^2}-1}{frac{2cos(alpha)}{sin(alpha)}}=frac{ctg(alpha)^2-1}{2ctg(alpha)};$$
В первой части на ЕГЭ попадаются номера на преобразование тригонометрических выражений, где часто содержится двойной угол:
Пример 6
Найти значение (24cos(2alpha)=?), если (sin(alpha)=-0,2.)
Воспользуемся формулой косинуса двойного угла:
$$cos(2alpha)=1-2sin(alpha)^2;$$
$$24cos(2alpha)=24(1-2sin(alpha)^2)=24-48sin(alpha)^2=24-48*(-0,2)^2=24-48*0,04=22,08.$$
Пример 7
Найти значение (frac{10sin(6alpha)}{3cos(3alpha)}=?), если (sin(3alpha)=0,6.)
Используем синус двойного угла, для этого представим (6alpha=2*(3alpha)):
$$sin(6alpha)=sin(2*(3alpha))=2sin(3alpha)cos(3alpha);$$
$$frac{10sin(6alpha)}{3cos(3alpha)}=frac{10*2sin(3alpha)cos(3alpha)}{3cos(3alpha)}=frac{20sin(3alpha)}{3}=frac{20*0,6}{3}=frac{12}{3}=4.$$
Пример 8
Найти значение выражения (frac{12sin(11^o)cos(11^o)}{sin(22^o)}=?)
Замечаем, что (22^o=2*11^o) и воспользуемся синусом двойного угла:
$$frac{12sin(11^o)cos(11^o)}{sin(22^o)}=frac{12sin(11^o)cos(11^o)}{2sin(11^o)cos(11^o)}=frac{12}{2}=6.$$
Формулы тройного угла
Формулы тройного угла обычно попадаются на математических олимпиадах или вступительных экзаменах в математические ВУЗы. Учить их необязательно, но знать о существовании полезно, тем более, что они достаточно легко выводятся.
$$cos(3*alpha)=cos(alpha)^3-3*sin(alpha)^2*cos(alpha)=-3*cos(alpha)+4*cos(alpha)^3;$$
$$sin(3*alpha)=3*sin(alpha)*cos(alpha)^2-sin(alpha)^3=3*sin(alpha)-4*sin(alpha)^3;$$
$$tg(3*alpha)=frac{3*tg(alpha)-tg(alpha)^3}{1-3*tg(alpha)^2};$$
$$ctg(3*alpha)=frac{ctg(alpha)^3-3*ctg(alpha)}{3*ctg(alpha)^2-1};$$
Выведем эти формулы, использую формулы сложения. Начнем с косинуса тройного угла:
$$cos(3*alpha)=cos(2alpha+alpha)=cos(2alpha)*cos(alpha)-sin(2alpha)*sin(alpha)=$$
$$=(cos(alpha)^2-sin(alpha)^2)*cos(alpha)-2sin(alpha)*cos(alpha)*sin(alpha)=$$
$$=cos(alpha)^3-sin(alpha)^2*cos(alpha)-2sin(alpha)^2*cos(alpha)=$$
$$=cos(alpha)^3-3sin(alpha)^2*cos(alpha);$$
Если расписать (sin(alpha)^2=1-cos(alpha)^2), то получим еще один вариант формулы тройного угла:
$$cos(3*alpha)=cos(alpha)^3-3sin(alpha)^2*cos(alpha)=cos(alpha)^3-3(1-cos(alpha)^2)*cos(alpha)=$$
$$=4cos(alpha)^3-3cos(alpha);$$
Аналогично выводится формула синуса тройного угла:
$$sin(3alpha)=sin(2alpha+alpha)=sin(2alpha)*cos(alpha)+sin(alpha)*cos(2alpha)=$$
$$=2sin(alpha)*cos(alpha)*cos(alpha)+sin(alpha)*(cos(alpha)^2-sin(alpha)^2)=$$
$$=2sin(alpha)*cos(alpha)^2+sin(alpha)*cos(alpha)^2-sin(alpha)^3=3sin(alpha)*cos(alpha)^2-sin(alpha)^3;$$
Распишем по основному тригонометрическому тождеству (cos(alpha)^2=1-sin(alpha)^2) и подставим:
$$sin(3alpha)=3sin(alpha)*cos(alpha)^2-sin(alpha)^3=$$
$$=3sin(alpha)*(1-sin(alpha)^2)-sin(alpha)^3=3sin(alpha)-4sin(alpha)^3;$$
Для тангенса и котангенса формулы тройного угла здесь выводить не будем, так как они достаточно редки. Но в качестве упражнения можете сами выполнить вывод, представив тангенс или котангенс по определению: через отношение синуса тройного угла к косинусу тройного угла или наоборот соотвественно.
Формулы тройного угла обычно используются при преобразовании сложных тригонометрических выражений. Например, на вступительных экзаменах в МФТИ любят давать тригонометрические уравнения на тройной угол и больше.
Формулы половинного угла (двойного аргумента)
$$sin(frac{alpha}{2})^2=frac{1-cos(alpha)}{2};$$
$$cos(frac{alpha}{2})^2=frac{1+cos(alpha)}{2};$$
$$tg(frac{alpha}{2})^2=frac{1-cos(alpha)}{1+cos(alpha)};$$
$$ctg(frac{alpha}{2})^2=frac{1+cos(alpha)}{1-cos(alpha)};$$
Формулы половинного угла это по сути формулы обратные формулам двойного угла. Достаточно запомнить их элементарный вывод, тогда учить совсем необязательно. Здесь важный момент, что любой угол (alpha) всегда можно представить в виде удвоенного угла (frac{alpha}{2}):
$$alpha=2*frac{alpha}{2};$$
Выведем формулу синуса половинного угла, для этого нам понадобится формула косинуса двойного угла:
$$cos(alpha)=1-2*sin(frac{alpha}{2})^2;$$
Выразим отсюда (sin(frac{alpha}{2})):
$$sin(frac{alpha}{2})^2=frac{1-cos(alpha)}{2};$$
Иногда эту формулу записывают без квадрата:
$$sin(frac{alpha}{2})=pmsqrt{frac{1-cos(alpha)}{2}};$$
Плюс минус возникает при избавлении от квадрата.
Вывод косинуса половинного угла тоже получается из формулы косинуса двойного угла:
$$cos(alpha)=2*cos(frac{alpha}{2})^2-1;$$
$$cos(frac{alpha}{2})^2=frac{cos(alpha)+1}{2};$$
$$cos(frac{alpha}{2})=pmsqrt{frac{cos(alpha)+1}{2}};$$
Доказательство формул половинного угла для тангенса и котангенса следует из выше доказанных формул:
$$tg(frac{alpha}{2})=frac{sin(frac{alpha}{2})}{cos(frac{alpha}{2})}=frac{pmsqrt{frac{1-cos(alpha)}{2}}}{pmsqrt{frac{cos(alpha)+1}{2}}}=sqrt{frac{frac{1-cos(alpha)}{2}}{frac{cos(alpha)+1}{2}}}=frac{1-cos(alpha)}{1+cos(alpha)};$$
Точно так же для котангенса:
$$сtg(frac{alpha}{2})=frac{cos(frac{alpha}{2})}{sin(frac{alpha}{2})}=frac{pmsqrt{frac{cos(alpha)+1}{2}}}{pmsqrt{frac{1-cos(alpha)}{2}}}=sqrt{frac{frac{cos(alpha)+1}{2}}{frac{1-cos(alpha)}{2}}}=frac{1+cos(alpha)}{1-cos(alpha)};$$
Пример 9
При помощи формул половинного угла можно, например, посчитать (cos(15^o)):
$$cos(frac{alpha}{2})^2=frac{1+cos(alpha)}{2};$$
$$cos(15^o)^2=frac{1+cos(30^o)}{2}=frac{1+frac{sqrt{3}}{2}}{2}=frac{2+sqrt{3}}{4};$$
$$cos(15^o)=sqrt{frac{2+sqrt{3}}{4}}.$$
Кстати, формулы половинного угла справедливы не только в явном виде, когда аргумент правой части формулы (alpha), а левой (frac{alpha}{2}). Но и в неявном, достаточно, чтобы аргумент правой части был больше аргумента левой в два раза:
$$sin(5alpha)=pmsqrt{frac{1-cos(10alpha)}{2}};$$
Формулы понижения степени
$$sin(alpha)^2=frac{1-cos(2*alpha)}{2};$$
$$cos(alpha)^2=frac{1+cos(2*alpha)}{2};$$
$$sin(alpha)^3=frac{3*sin(alpha)-sin(3*alpha)}{4};$$
$$cos(alpha)^3=frac{3*cos(alpha)+cos(3*alpha)}{4};$$
$$sin(alpha)^4=frac{3-4*cos(2*alpha)+cos(4*alpha)}{8};$$
$$cos(alpha)^4=frac{3+4*cos(2*alpha)+cos(4*alpha)}{8};$$
Формулы понижения второй степени на самом деле дублируют формулы половинного угла.
Формулы понижения третей степени перестановкой слагаемых дублируют формулы тройного угла.
Преобразование суммы и разности тригонометрических функций:
$$sin(alpha)+sin(beta)=2*sinleft(frac{alpha+beta}{2}right)*cosleft(frac{alpha-beta}{2}right);$$
$$sin(alpha)-sin(beta)=2*sinleft(frac{alpha-beta}{2}right)*cosleft(frac{alpha+beta}{2}right);$$
$$cos(alpha)+cos(beta)=2*cosleft(frac{alpha+beta}{2}right)*cosleft(frac{alpha-beta}{2}right);$$
$$cos(alpha)-cos(beta)=-2*sinleft(frac{alpha+beta}{2}right)*sinleft(frac{alpha-beta}{2}right);$$
$$cos(alpha)-cos(beta)=2*sinleft(frac{alpha+beta}{2}right)*sinleft(frac{beta-alpha}{2}right);$$
$$tg(alpha)+tg(beta)=frac{sin(alpha+beta)}{cos(alpha)*cos(beta)};$$
$$tg(alpha)-tg(beta)=frac{sin(alpha-beta)}{cos(alpha)*cos(beta)};$$
$$ctg(alpha)+ctg(beta)=frac{sin(alpha+beta)}{sin(alpha)*sin(beta)};$$
$$ctg(alpha)-ctg(beta)=frac{sin(beta-alpha)}{sin(alpha)*sin(beta)};$$
Формулы для суммы и разности тригонометрических функций полезны, если необходимо превратить сумму двух функций в произведение. Они в основном используются в уравнениях и преобразованиях сложных выражений, когда необходимо слагаемые разложить на множители.
Для вывода формул суммы и разности синусов и косинусов нам понадобится пара трюков и формулы синуса и косинуса суммы и разности (тут можно запутаться, в названиях формул, будьте внимательны). Вывод получается не самый очевидный.
Обратите внимание, что любой угол (alpha) можно представить в таком странном виде:
$$alpha=frac{alpha}{2}+frac{alpha}{2}+frac{beta}{2}-frac{beta}{2}=frac{alpha+beta}{2}+frac{alpha-beta}{2};$$
Аналогично угол (beta):
$$beta=frac{alpha+beta}{2}-frac{alpha-beta}{2};$$
Эти странности нам понадобятся при выводе формул, просто обратите на них внимание.
А теперь перейдем непосредственно к выводу формулы суммы синусов двух углов. Для начала распишем угла (alpha) и (beta) по формулам выше:
$$sin(alpha)+sin(beta)=sin(frac{alpha+beta}{2}+frac{alpha-beta}{2})+sin(frac{alpha+beta}{2}-frac{alpha-beta}{2}); qquad (*)$$
Теперь воспользуемся формулами синуса суммы и синуса разности:
$$sin(gamma+sigma)=sin(gamma)*cos(sigma)+sin(sigma)*cos(gamma);$$
$$sin(gamma-sigma)=sin(gamma)*cos(sigma)-sin(sigma)*cos(gamma);$$
Только у нас под синусами будут стоять не (gamma) и (sigma), а целые выражения.
Пусть:
$$gamma=frac{alpha+beta}{2};$$
$$sigma=frac{alpha-beta}{2};$$
Применим формулы синуса суммы и разности в (*):
$$sin(alpha)+sin(beta)=sin(frac{alpha+beta}{2}+frac{alpha-beta}{2})+sin(frac{alpha+beta}{2}-frac{alpha-beta}{2})=$$
$$=left(sin(frac{alpha+beta}{2})*cos(frac{alpha-beta}{2})+sin(frac{alpha-beta}{2})*cos(frac{alpha+beta}{2})right)+$$
$$+left(sin(frac{alpha+beta}{2})*cos(frac{alpha-beta}{2})-sin(frac{alpha-beta}{2})*cos(frac{alpha+beta}{2})right)=$$
$$=2*sin(frac{alpha+beta}{2})*cos(frac{alpha-beta}{2}); $$
В самом конце мы просто раскрыли большие скобки и привели подобные слагаемые.
Аналогично выводятся все остальные формулы.
Пример 10
Вычислить (sin(165)+sin(75)=?)
(165^o) и (75^o) это не табличные углы. Значения синусов этих углов мы не знаем. Для решения этого примера воспользуемся формулой суммы синусов:
$$sin(alpha)+sin(beta)=2*sinleft(frac{alpha+beta}{2}right)*cosleft(frac{alpha-beta}{2}right);$$
$$sin(165^o)+sin(75^o)=2*sinleft(frac{165^o+75^o}{2}right)*cosleft(frac{165^o-75^o}{2}right)=$$
$$=2*sin(120^o)*cos(45^o)=2*frac{sqrt{3}}{2}*frac{sqrt{2}}{2}=frac{sqrt{6}}{2}.$$
Преобразование произведения тригонометрических функций
$$sin(alpha)*sin(beta)=frac{1}{2}*left(cos(alpha-beta)-cos(alpha+beta)right);$$
$$cos(alpha)*cos(beta)=frac{1}{2}*left(cos(alpha-beta)+cos(alpha+beta)right);$$
$$sin(alpha)*cos(beta)=frac{1}{2}*left(sin(alpha-beta)+sin(alpha+beta)right);$$
В некотором смысле формулы произведения синуса, косинуса, тангенса и котангенса являются обратными к тригонометрическим формулам суммы и разности тригонометрических функций. При помощи этих формул возможно перейти от произведения к сумме или разности.
Для вывода нам опять понадобятся формулы косинуса суммы и разности:
$$cos(alpha+beta)=cos(alpha)*cos(beta)-sin(beta)*sin(alpha);$$
$$cos(alpha-beta)=cos(alpha)*cos(beta)+sin(beta)*sin(alpha);$$
Сложим эти две формулы. Для этого складываем их левые части и приравниваем сумме правых частей:
$$cos(alpha+beta)+cos(alpha-beta)=cos(alpha)*cos(beta)-sin(beta)*sin(alpha)+cos(alpha)*cos(beta)+sin(beta)*sin(alpha);$$
Приводим подобные слагаемые:
$$cos(alpha+beta)+cos(alpha-beta)=2*cos(alpha)*cos(beta);$$
Отсюда получаем:
$$cos(alpha)*cos(beta)=frac{1}{2}*(cos(alpha+beta)+cos(alpha-beta));$$
Формула произведения косинусов доказана.
Произведение синусов доказывается похожим образом. Для этого домножим формулу косинуса суммы слева и справа на ((-1)):
$$-cos(alpha+beta)=-cos(alpha)*cos(beta)+sin(beta)*sin(alpha);$$
Косинус разности оставим без изменений:
$$cos(alpha-beta)=cos(alpha)*cos(beta)+sin(beta)*sin(alpha);$$
Сложим опять эти две формулы:
$$cos(alpha-beta)-cos(alpha+beta)=cos(alpha)*cos(beta)+sin(beta)*sin(alpha)-cos(alpha)*cos(beta)+sin(beta)*sin(alpha);$$
$$cos(alpha-beta)-cos(alpha+beta)=2*sin(beta)*sin(alpha);$$
$$sin(beta)*sin(alpha)=frac{1}{2}*(cos(alpha-beta)-cos(alpha+beta));$$
Произведение синусов тоже доказано.
Для того, чтобы вывести формулу произведения синуса и косинуса, нам понадобятся формулы синуса суммы и разности:
$$sin(alpha+beta)=sin(alpha)*cos(beta)+sin(beta)*cos(alpha);$$
$$sin(alpha-beta)=sin(alpha)*cos(beta)-sin(beta)*cos(alpha);$$
Сложим их:
$$sin(alpha+beta)+sin(alpha-beta)=sin(alpha)*cos(beta)+sin(beta)*cos(alpha)+sin(alpha)*cos(beta)-sin(beta)*cos(alpha);$$
$$sin(alpha+beta)+sin(alpha-beta)=2*sin(alpha)*cos(beta);$$
$$sin(alpha)*cos(beta)=frac{1}{2}*(sin(alpha+beta)+sin(alpha-beta));$$
Пример 11
Вычислить (sin(75^o)*cos(15^o)=?)
Воспользуемся формулой произведения синуса и косинуса:
$$sin(alpha)*cos(beta)=frac{1}{2}*(sin(alpha+beta)+sin(alpha-beta));$$
$$sin(75^o)*cos(15^o)=frac{1}{2}*(sin(75^o+15^o)+sin(75^o-15^o))=$$
$$=frac{1}{2}*(sin(90^o)+sin(60^o))=frac{1}{2}*(1+frac{sqrt{3}}{2})=frac{2+sqrt{3}}{4}.$$
Таблица синусов и как ей пользоваться – с примерами решения задач
Одной из самых часто используемых из всех тригонометрических таблиц Брадиса, является таблица синусов. В этой статье мы разберемся с таким понятием, как синус (sin), научимся находить значения синуса для различных углов (0, 30, 45, 60, 90), и поймем, для чего нужна таблица синусов.
Таблица синусов и её применение
Для начала нужно напомнить, что означает такое понятие, как синус угла.
Синус – это отношение противолежащего этому углу катета к гипотенузе.
Это справедливо в случае, если треугольник прямоугольный.
Пример: найдем синус угла ⍺ и угла β
sin ⍺ = а/с или отношение стороны ВС к стороне АВ. Если брать угол β, то противостоящим будет считаться сторона b или АС. Гипотенуза в данном случае та же – AB. Тогда:
sin β = b/с или АС отношение АВ.
В прямоугольном треугольнике всегда 2 катета и только одна гипотенуза
Как известно, целых значений угла – 360. Но часто нужно рассчитать значения для самых популярных углов, таких как: синус 0°, синус 30°, синус 45°, синус 60°, синус 90°. Эти значения можно найти в таблицах Брадиса.
Несмотря на то, что в 2021 году она отмечает свой столетний юбилей, свою актуальность таблица Брадиса не утратила. В частности ее применяют архитекторы, проектанты, конструктора для проведения быстрых промежуточных расчетов. Таблицы Брадиса разрешены к использованию в школах при сдаче ЕГЭ, в отличие от калькуляторов.
Как рассчитать синус угла
Некоторые значения синуса угла можно рассчитать достаточно просто, воспользовавшись таблицей синусов угла π (пи) в радианах.
Пример: рассчитаем значения синуса следующих углов: 0°, 30°, 45°, 60°, 90° в радианах с использованием π (пи)
Берем синус 0°, в радианах он будет 0 , тут даже считать нечего.
Синус 30° равен π/6 .
Потому что “все” π (пи) – это половина окружности или 180°. Поэтому 30° – это все 180° разделенные на 6. По таком же принципу находим значения синусов для остальных углов.
Синус 45° равен π/4 (180 градусов разделенные на 4).
Синус 60° равен π/3 (180 градусов разделенные на 3).
Синус 90° равен π/2 или 1 (180 градусов разделенные на 2).
Остальное дело калькулятора – просто переводим π в 3,14 и делим на нужное число 6, 4, 3 или 2.
Но часто нужно решить задачу для каких то либо целей, при котором значения углов будут другими. Посмотрим пример решения такой задачи.
Пример: рассмотрим прямоугольный треугольник, в котором катеты а и b имеют значение 5 и 2√6, нужно найти синус каждого острого угла. Рисунок и обозначения стандартные (смотри выше).
Используя теорему Пифагора, которая гласит, что “квадрат гипотенузы равен сумме квадратов двух катетов”, находим гипотенузу:
С₂=5х5+ (2√6)х(2√6) = 25 + 4х6 = 49 (см). Итог: С₂ = 7 (см).
Нам известно, что синус это есть отношение катета, который противолежит к искомому углу, к гипотенузе. То есть sin α = a/c, это значит, что sin α =5/7. Соответственно, sin β= b/с ,и sin β равен 2√6/7.
Теперь пробуем найти точное значение синуса и через таблицы Брадиса, найдя число 5/7, затем по таблице найти соответствующее ему значение угла в градусах. Потом от 90° отнимаем это значение, получаем градусы и переводим его в радианы.
Можно использовать формулу из теоремы синусов.
Её можно использовать в случае, если у нас известна гипотенуза треугольника и два угла или один из катетов. Тогда в соответствии с правилами пропорции находим:
Что найти синус угла, к примеру: α = 42°, угол β =48 °, открываем таблицу Брадиса. Так как у нас углы без минут, находим значение синуса угла по первой колонке. Sin α = 0,6691, sin β = 0,7431. Пусть в условии сторона с = 9 см, Синус 90° = 1. Подставляем значение и получаем: а = 9 х (0,6691: 1) = 6, 0219 (см).
Что такое таблица синусов π и таблица Брадиса
В таблице синусов значение угла α дается в:
- радианах,
- градусах,
- в виде числа, выраженного через квадратный корень.
Это таблица не только для синусов, но и для других тригонометрических знаков.
Рассчитываем калькулятором значение π, данные можно посмотреть в таблице. Здесь включены значения синуса, которых нет в таблицах Брадиса, вычисления сделаны с точностью до 4 знака. Если нужно узнать, чему равен синус, это всегда можно посмотреть в таблице или рассчитать самому . Как пользоваться таблицей Бралиса , можно прочитать в моей статье, перейдя по ссылке. Там есть примеры задач и расчёты.
Как пользоваться таблицей Брадиса для синусов
Если у вас стоит вопрос, как пользоваться таблицей Брадиса, для нахождения синуса угла, рассмотрим такой пример.
Источник статьи: http://zen.yandex.ru/media/ideika/tablica-sinusov-i-kak-ei-polzovatsia-s-primerami-resheniia-zadach-5edcc375e8e24e636af5032f
Что такое синус, косинус, тангенс и котангенс в прямоугольном треугольнике?
Синус, косинус и тангенс острого угла прямоугольного треугольника.
Сейчас рассмотрим что же такое синус, косинус, тангенс и котангенс в прямоугольном треугольнике?
Это тема не сложная, главное это запомнить правила. И так начнем:
Вспомним, что такое прямоугольный треугольник?
Прямоугольным треугольником, называется треугольник у которого один из углов прямой (составляет 90 градусов). Две стороны которые прилежат к прямому углу, называются катетами, а сторона лежащая напротив прямого угла, называется гипотенузой.
Определение:
Синус (sin(a)) — это отношение противолежащего катета к гипотенузе;
Косинус (cos(a)) — это отношение прилежащего катета к гипотенузе;
Тангенс (tg(a)) — это отношение противолежащего катета к прилежащему катету;
Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу;
tg(a)=sin(a)/cos(a)
Котангенс (ctg(a)) — это отношение прилежащего катета к противолежащему.
Другое (равносильное) определение: котангенсом острого угла называется отношение косинуса угла к его синусу;
ctg(a)=cos(a)/sin(a)
Рассмотрим на примере:
Пусть дан прямоугольный треугольник ABC с прямым углом C.
sin(a)=BC/AB
cos(a)=AC/AB
tg(a)=BC/AC
ctg(a)=AC/BC
Источник статьи: http://zen.yandex.ru/media/id/5c950d5bbde70300b469fb12/chto-takoe-sinus-kosinus-tangens-i-kotangens-v-priamougolnom-treugolnike-5c9db7a4fa932f00b4b39c59
Таблица СИНУСОВ для углов от 0° до 360° градусов
СИНУС (SIN α) — это одна из прямых тригонометрических функций для углов, в прямоугольном треугольнике синус острого угла равен отношению противолежащего катета к его единственной гипотенузе.
Малая таблица значений тригонометрических функций (в радианах и градусах)
| α (радианы) | 0 | π/6 | π/4 | π/3 | π/2 | π | √3π/2 | 2π |
|---|---|---|---|---|---|---|---|---|
| α (градусы) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| SIN α (СИНУС) | 0 | 1/2 | √ 2/2 | √3 /2 | 1 | 0 | -1 | 0 |
Полная таблица синусов для углов от 0° до 360° с шагом всего в 1°
| Угол в градусах | Sin (Синус) |
|---|---|
| 0° | 0 |
| 1° | 0.0175 |
| 2° | 0.0349 |
| 3° | 0.0523 |
| 4° | 0.0698 |
| 5° | 0.0872 |
| 6° | 0.1045 |
| 7° | 0.1219 |
| 8° | 0.1392 |
| 9° | 0.1564 |
| 10° | 0.1736 |
| 11° | 0.1908 |
| 12° | 0.2079 |
| 13° | 0.225 |
| 14° | 0.2419 |
| 15° | 0.2588 |
| 16° | 0.2756 |
| 17° | 0.2924 |
| 18° | 0.309 |
| 19° | 0.3256 |
| 20° | 0.342 |
| 21° | 0.3584 |
| 22° | 0.3746 |
| 23° | 0.3907 |
| 24° | 0.4067 |
| 25° | 0.4226 |
| 26° | 0.4384 |
| 27° | 0.454 |
| 28° | 0.4695 |
| 29° | 0.4848 |
| 30° | 0.5 |
| 31° | 0.515 |
| 32° | 0.5299 |
| 33° | 0.5446 |
| 34° | 0.5592 |
| 35° | 0.5736 |
| 36° | 0.5878 |
| 37° | 0.6018 |
| 38° | 0.6157 |
| 39° | 0.6293 |
| 40° | 0.6428 |
| 41° | 0.6561 |
| 42° | 0.6691 |
| 43° | 0.682 |
| 44° | 0.6947 |
| 45° | 0.7071 |
| 46° | 0.7193 |
| 47° | 0.7314 |
| 48° | 0.7431 |
| 49° | 0.7547 |
| 50° | 0.766 |
| 51° | 0.7771 |
| 52° | 0.788 |
| 53° | 0.7986 |
| 54° | 0.809 |
| 55° | 0.8192 |
| 56° | 0.829 |
| 57° | 0.8387 |
| 58° | 0.848 |
| 59° | 0.8572 |
| 60° | 0.866 |
| 61° | 0.8746 |
| 62° | 0.8829 |
| 63° | 0.891 |
| 64° | 0.8988 |
| 65° | 0.9063 |
| 66° | 0.9135 |
| 67° | 0.9205 |
| 68° | 0.9272 |
| 69° | 0.9336 |
| 70° | 0.9397 |
| 71° | 0.9455 |
| 72° | 0.9511 |
| 73° | 0.9563 |
| 74° | 0.9613 |
| 75° | 0.9659 |
| 76° | 0.9703 |
| 77° | 0.9744 |
| 78° | 0.9781 |
| 79° | 0.9816 |
| 80° | 0.9848 |
| 81° | 0.9877 |
| 82° | 0.9903 |
| 83° | 0.9925 |
| 84° | 0.9945 |
| 85° | 0.9962 |
| 86° | 0.9976 |
| 87° | 0.9986 |
| 88° | 0.9994 |
| 89° | 0.9998 |
| 90° | 1 |
Полная таблица синусов для углов от 91° до 180°
| Угол в градусах | Sin (Синус) |
|---|---|
| 91° | 0.9998 |
| 92° | 0.9994 |
| 93° | 0.9986 |
| 94° | 0.9976 |
| 95° | 0.9962 |
| 96° | 0.9945 |
| 97° | 0.9925 |
| 98° | 0.9903 |
| 99° | 0.9877 |
| 100° | 0.9848 |
| 101° | 0.9816 |
| 102° | 0.9781 |
| 103° | 0.9744 |
| 104° | 0.9703 |
| 105° | 0.9659 |
| 106° | 0.9613 |
| 107° | 0.9563 |
| 108° | 0.9511 |
| 109° | 0.9455 |
| 110° | 0.9397 |
| 111° | 0.9336 |
| 112° | 0.9272 |
| 113° | 0.9205 |
| 114° | 0.9135 |
| 115° | 0.9063 |
| 116° | 0.8988 |
| 117° | 0.891 |
| 118° | 0.8829 |
| 119° | 0.8746 |
| 120° | 0.866 |
| 121° | 0.8572 |
| 122° | 0.848 |
| 123° | 0.8387 |
| 124° | 0.829 |
| 125° | 0.8192 |
| 126° | 0.809 |
| 127° | 0.7986 |
| 128° | 0.788 |
| 129° | 0.7771 |
| 130° | 0.766 |
| 131° | 0.7547 |
| 132° | 0.7431 |
| 133° | 0.7314 |
| 134° | 0.7193 |
| 135° | 0.7071 |
| 136° | 0.6947 |
| 137° | 0.682 |
| 138° | 0.6691 |
| 139° | 0.6561 |
| 140° | 0.6428 |
| 141° | 0.6293 |
| 142° | 0.6157 |
| 143° | 0.6018 |
| 144° | 0.5878 |
| 145° | 0.5736 |
| 146° | 0.5592 |
| 147° | 0.5446 |
| 148° | 0.5299 |
| 149° | 0.515 |
| 150° | 0.5 |
| 151° | 0.4848 |
| 152° | 0.4695 |
| 153° | 0.454 |
| 154° | 0.4384 |
| 155° | 0.4226 |
| 156° | 0.4067 |
| 157° | 0.3907 |
| 158° | 0.3746 |
| 159° | 0.3584 |
| 160° | 0.342 |
| 161° | 0.3256 |
| 162° | 0.309 |
| 163° | 0.2924 |
| 164° | 0.2756 |
| 165° | 0.2588 |
| 166° | 0.2419 |
| 167° | 0.225 |
| 168° | 0.2079 |
| 169° | 0.1908 |
| 170° | 0.1736 |
| 171° | 0.1564 |
| 172° | 0.1392 |
| 173° | 0.1219 |
| 174° | 0.1045 |
| 175° | 0.0872 |
| 176° | 0.0698 |
| 177° | 0.0523 |
| 178° | 0.0349 |
| 179° | 0.0175 |
| 180° | 0 |
Таблица синусов для углов 181° — 270°
| Угол | Sin (Синус) |
|---|---|
| 181° | -0.0175 |
| 182° | -0.0349 |
| 183° | -0.0523 |
| 184° | -0.0698 |
| 185° | -0.0872 |
| 186° | -0.1045 |
| 187° | -0.1219 |
| 188° | -0.1392 |
| 189° | -0.1564 |
| 190° | -0.1736 |
| 191° | -0.1908 |
| 192° | -0.2079 |
| 193° | -0.225 |
| 194° | -0.2419 |
| 195° | -0.2588 |
| 196° | -0.2756 |
| 197° | -0.2924 |
| 198° | -0.309 |
| 199° | -0.3256 |
| 200° | -0.342 |
| 201° | -0.3584 |
| 202° | -0.3746 |
| 203° | -0.3907 |
| 204° | -0.4067 |
| 205° | -0.4226 |
| 206° | -0.4384 |
| 207° | -0.454 |
| 208° | -0.4695 |
| 209° | -0.4848 |
| 210° | -0.5 |
| 211° | -0.515 |
| 212° | -0.5299 |
| 213° | -0.5446 |
| 214° | -0.5592 |
| 215° | -0.5736 |
| 216° | -0.5878 |
| 217° | -0.6018 |
| 218° | -0.6157 |
| 219° | -0.6293 |
| 220° | -0.6428 |
| 221° | -0.6561 |
| 222° | -0.6691 |
| 223° | -0.682 |
| 224° | -0.6947 |
| 225° | -0.7071 |
| 226° | -0.7193 |
| 227° | -0.7314 |
| 228° | -0.7431 |
| 229° | -0.7547 |
| 230° | -0.766 |
| 231° | -0.7771 |
| 232° | -0.788 |
| 233° | -0.7986 |
| 234° | -0.809 |
| 235° | -0.8192 |
| 236° | -0.829 |
| 237° | -0.8387 |
| 238° | -0.848 |
| 239° | -0.8572 |
| 240° | -0.866 |
| 241° | -0.8746 |
| 242° | -0.8829 |
| 243° | -0.891 |
| 244° | -0.8988 |
| 245° | -0.9063 |
| 246° | -0.9135 |
| 247° | -0.9205 |
| 248° | -0.9272 |
| 249° | -0.9336 |
| 250° | -0.9397 |
| 251° | -0.9455 |
| 252° | -0.9511 |
| 253° | -0.9563 |
| 254° | -0.9613 |
| 255° | -0.9659 |
| 256° | -0.9703 |
| 257° | -0.9744 |
| 258° | -0.9781 |
| 259° | -0.9816 |
| 260° | -0.9848 |
| 261° | -0.9877 |
| 262° | -0.9903 |
| 263° | -0.9925 |
| 264° | -0.9945 |
| 265° | -0.9962 |
| 266° | -0.9976 |
| 267° | -0.9986 |
| 268° | -0.9994 |
| 269° | -0.9998 |
| 270° | -1 |
Таблица синусов для углов от 271° до 360°
| Угол | Sin (Синус) |
|---|---|
| 271° | -0.9998 |
| 272° | -0.9994 |
| 273° | -0.9986 |
| 274° | -0.9976 |
| 275° | -0.9962 |
| 276° | -0.9945 |
| 277° | -0.9925 |
| 278° | -0.9903 |
| 279° | -0.9877 |
| 280° | -0.9848 |
| 281° | -0.9816 |
| 282° | -0.9781 |
| 283° | -0.9744 |
| 284° | -0.9703 |
| 285° | -0.9659 |
| 286° | -0.9613 |
| 287° | -0.9563 |
| 288° | -0.9511 |
| 289° | -0.9455 |
| 290° | -0.9397 |
| 291° | -0.9336 |
| 292° | -0.9272 |
| 293° | -0.9205 |
| 294° | -0.9135 |
| 295° | -0.9063 |
| 296° | -0.8988 |
| 297° | -0.891 |
| 298° | -0.8829 |
| 299° | -0.8746 |
| 300° | -0.866 |
| 301° | -0.8572 |
| 302° | -0.848 |
| 303° | -0.8387 |
| 304° | -0.829 |
| 305° | -0.8192 |
| 306° | -0.809 |
| 307° | -0.7986 |
| 308° | -0.788 |
| 309° | -0.7771 |
| 310° | -0.766 |
| 311° | -0.7547 |
| 312° | -0.7431 |
| 313° | -0.7314 |
| 314° | -0.7193 |
| 315° | -0.7071 |
| 316° | -0.6947 |
| 317° | -0.682 |
| 318° | -0.6691 |
| 319° | -0.6561 |
| 320° | -0.6428 |
| 321° | -0.6293 |
| 322° | -0.6157 |
| 323° | -0.6018 |
| 324° | -0.5878 |
| 325° | -0.5736 |
| 326° | -0.5592 |
| 327° | -0.5446 |
| 328° | -0.5299 |
| 329° | -0.515 |
| 330° | -0.5 |
| 331° | -0.4848 |
| 332° | -0.4695 |
| 333° | -0.454 |
| 334° | -0.4384 |
| 335° | -0.4226 |
| 336° | -0.4067 |
| 337° | -0.3907 |
| 338° | -0.3746 |
| 339° | -0.3584 |
| 340° | -0.342 |
| 341° | -0.3256 |
| 342° | -0.309 |
| 343° | -0.2924 |
| 344° | -0.2756 |
| 345° | -0.2588 |
| 346° | -0.2419 |
| 347° | -0.225 |
| 348° | -0.2079 |
| 349° | -0.1908 |
| 350° | -0.1736 |
| 351° | -0.1564 |
| 352° | -0.1392 |
| 353° | -0.1219 |
| 354° | -0.1045 |
| 355° | -0.0872 |
| 356° | -0.0698 |
| 357° | -0.0523 |
| 358° | -0.0349 |
| 359° | -0.0175 |
| 360° | 0 |
Таблица синусов особенно нужна, когда у вас под рукой нет супер навороченного инженерного калькулятора с маленькой спасительной кнопкой с надписью «sin». В таком случае, чтобы узнать, чему же равняется синус определенного заданного угла, просто найдите информацию о интересующем градусе.
Как распечатать таблицу? Левой кнопкой на компьютерной мишке выделите полностью всё таблицу, на выделенном фоне нажмите уже правую кнопку мишки и в появившемся меню перейдете в пункт «Печать».
Как пользоваться таблицей? Всё гораздо проще, чем Вы думаете, ищем в левой вертикальной колонке, соответствующий градус, и напротив него и будет указано нужное значение синуса для данного нужного нам угла.
Чему равен синус 45? …
– А вот собственно и сам ответ на поставленную задачку.sin 45 = 0.7071
Источник статьи: http://kvn201.com.ua/table-of-sines.htm


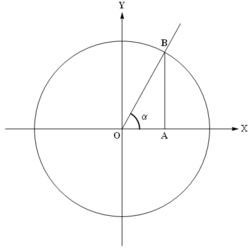












 — числа Бернулли,
— числа Бернулли, — числа Эйлера.
— числа Эйлера.






































 следует из формулы дополнения и формулы Гаусса для Гамма-функции
следует из формулы дополнения и формулы Гаусса для Гамма-функции














































 где
где 





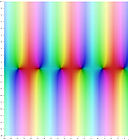
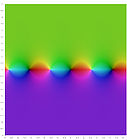


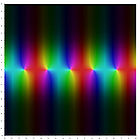







![{displaystyle {begin{aligned}sin z&=sin xcosh y+icos xsinh y\[5pt]cos z&=cos xcosh y-isin xsinh yend{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c1646655eab602e234f42df85cae241ffbb867cf)

![{displaystyle {begin{aligned}sin(x)&=x-{frac {x^{3}}{3!}}+{frac {x^{5}}{5!}}-{frac {x^{7}}{7!}}+cdots \[8pt]&=sum _{n=0}^{infty }{frac {(-1)^{n}}{(2n+1)!}}x^{2n+1}\[8pt]end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/def345e147219a7892eb8140dfeb1c77b29dce38)
![{displaystyle {begin{aligned}cos(x)&=1-{frac {x^{2}}{2!}}+{frac {x^{4}}{4!}}-{frac {x^{6}}{6!}}+cdots \[8pt]&=sum _{n=0}^{infty }{frac {(-1)^{n}}{(2n)!}}x^{2n}\[8pt]end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/72f8792e2fd4203f00339519200068cdd1652b08)









































 строится по координате y (красная точка) точки на единичной окружности (зеленого цвета) под углом θ.
строится по координате y (красная точка) точки на единичной окружности (зеленого цвета) под углом θ.
















 OEIS : A019812
OEIS : A019812  OEIS : A019815
OEIS : A019815  OEIS : A019818
OEIS : A019818  OEIS : A019821
OEIS : A019821  OEIS : A019827
OEIS : A019827  OEIS : A019830
OEIS : A019830  = грех (22,5 ∘) = 2–2 2 { displaystyle sin left ({ frac { pi} {8}} right) = sin (22,5 ^ { circ}) = { frac { sqrt {2 — { sqrt {2}}}} {2}}}
= грех (22,5 ∘) = 2–2 2 { displaystyle sin left ({ frac { pi} {8}} right) = sin (22,5 ^ { circ}) = { frac { sqrt {2 — { sqrt {2}}}} {2}}}
 OEIS : A019833
OEIS : A019833  OEIS : A019836
OEIS : A019836  OEIS : A019842
OEIS : A019842  OEIS : A019845
OEIS : A019845  OEIS : A019848
OEIS : A019848  OEIS : A019851
OEIS : A019851 






 can be decomposed as
can be decomposed as![{ displaystyle cos (zx) = { frac {z sin ( pi z)} { pi}} displaystyle sum _ {n = - infty} ^ { infty} { frac {(-1) ^ {n} , e ^ {inx}} {z ^ { 2} -n ^ {2}}}, , z in mathbb {C} setminu s { mathbb {Z} }, , x in [- pi, pi].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/99f892c035938064b0ca52b732ef6265e86a052f)
 yields
yields

 is the derivative of ln ( sin ( π z)) + C 0 {displaystyle ln(sin(pi z))+C_{0}}
is the derivative of ln ( sin ( π z)) + C 0 {displaystyle ln(sin(pi z))+C_{0}} . Furthermore, if d f d z = z z 2 − n 2 {textstyle {frac {df}{dz}}={frac {z}{z^{2}-n^{2}}}}
. Furthermore, if d f d z = z z 2 − n 2 {textstyle {frac {df}{dz}}={frac {z}{z^{2}-n^{2}}}} , then the function f {displaystyle f}
, then the function f {displaystyle f} such that the emerged series converges is f = 1 2 ln ( 1 − z 2 / n 2) + C 1 {textstyle f={frac {1}{2}}ln(1-z^{2}/n^{2})+C_{1}}
such that the emerged series converges is f = 1 2 ln ( 1 − z 2 / n 2) + C 1 {textstyle f={frac {1}{2}}ln(1-z^{2}/n^{2})+C_{1}} , which can be proved using the Weierstrass M-test. The interchange of the sum and derivative is justified by uniform convergence. It follows that
, which can be proved using the Weierstrass M-test. The interchange of the sum and derivative is justified by uniform convergence. It follows that

 and lim z → 0 ∏ n = 1 ∞ ( 1 − z 2 n 2) = 1 {textstyle lim _{zto 0}prod _{n=1}^{infty }left(1-{frac {z^{2}}{n^{2}}}right)=1}
and lim z → 0 ∏ n = 1 ∞ ( 1 − z 2 n 2) = 1 {textstyle lim _{zto 0}prod _{n=1}^{infty }left(1-{frac {z^{2}}{n^{2}}}right)=1} , we have e C = π {displaystyle e^{C}=pi }
, we have e C = π {displaystyle e^{C}=pi } . Hence
. Hence
 . Let a n ( z) = − z 2 n 2 {displaystyle textstyle {a_{n}(z)=-{frac {z^{2}}{n^{2}}}}}
. Let a n ( z) = − z 2 n 2 {displaystyle textstyle {a_{n}(z)=-{frac {z^{2}}{n^{2}}}}} . Since ∑ n = 1 ∞ | a n ( z) | {displaystyle textstyle {sum _{n=1}^{infty }|a_{n}(z)|}}
. Since ∑ n = 1 ∞ | a n ( z) | {displaystyle textstyle {sum _{n=1}^{infty }|a_{n}(z)|}} converges uniformly on any closed disk, ∏ n = 1 ∞ ( 1 + a n ( z)) {displaystyle textstyle {prod _{n=1}^{infty }(1+a_{n}(z))}}
converges uniformly on any closed disk, ∏ n = 1 ∞ ( 1 + a n ( z)) {displaystyle textstyle {prod _{n=1}^{infty }(1+a_{n}(z))}} converges uniformly on any closed disk as well. It follows that the infinite product is holomorphic on C {displaystyle mathbb {C} }
converges uniformly on any closed disk as well. It follows that the infinite product is holomorphic on C {displaystyle mathbb {C} } , which completes the proof. ◼ {displaystyle blacksquare }
, which completes the proof. ◼ {displaystyle blacksquare }



