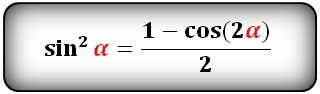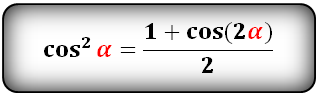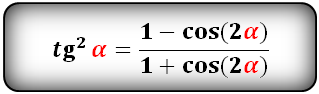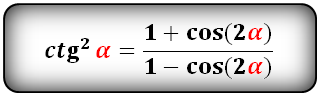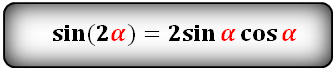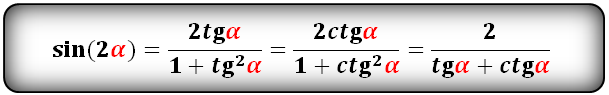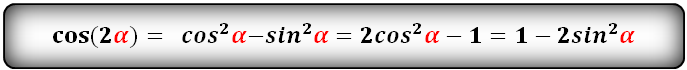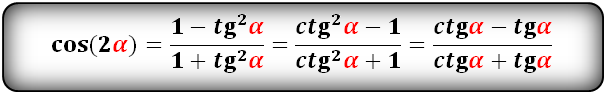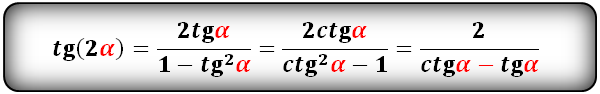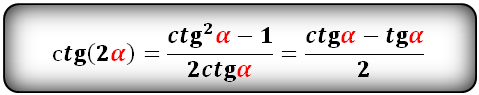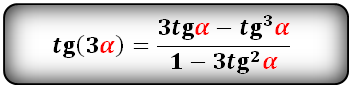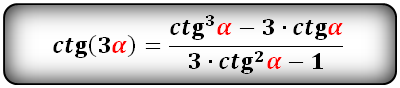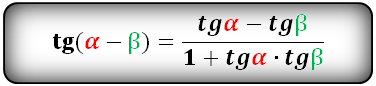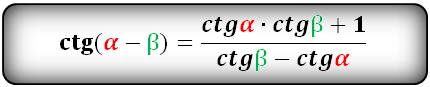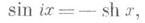Тригонометрия — раздел математической науки, в котором изучаются тригонометрические функции и их использование в геометрии. Развитие тригонометрии началось еще во времена античной Греции. Во времена средневековья важный вклад в развитие этой нужной науки внесли ученые Ближнего Востока и Индии, которые придумали наиболее важные понятия, объяснили многие свойства, предложили варианты измерения и др.
Данная статья посвящена базовым понятиям и дефинициям тригонометрии. В ней рассмотрены определения основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Разъяснен и проиллюстрирован их смысл в контексте геометрии без таблиц и графиков.
Синус, косинус, тангенс и котангенс. Определения
Зачем разделять понятия синуса, косинуса, тангенса и котангенса?
Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.
Что такое синус?
Синус угла (sin α) — это отношение противолежащего этому углу катета к гипотенузе.
Что такое косинус?
Косинус угла (cosα) — это отношение прилежащего катета к гипотенузе.
Что такое тангенс?
Тангенс угла (tg α) — это отношение противолежащего катета к прилежащему.
Котангенс угла (ctg α) — отношение прилежащего катета к противолежащему.
Данные определения даны для острого угла прямоугольного треугольника!
Синус и косинус можно представить через экспоненту (экспоненциальная функция).
Приведем иллюстрацию.
В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.
Означения синуса, косинуса, тангенса и котангенса позволяют вычислять (находить) значения этих функций по известным длинам сторон треугольника.
Что и почему важно и принято помнить в ходе такого нахождения?
Область значений синуса и косинуса: от -1 до 1. Иными словами синус и косинус принимают значения от -1 до 1. Область значений тг и ктг — вся числовая прямая, то есть эти функции могут принимать любые значения.
Как найти синус? Для начала нужно определиться, какой перед нами треугольник: прямоугольный или произвольный. В первом случае можно использовать обычный тригонометрический метод, а во втором — теорему косинусов.
Как найти косинус? Соответственно, нам нужно знать значения прилежающего катета и гипотенузы.
Как найти тангенс? Если треугольник прямоугольный, то тангенс вычисляется при помощи значений противоположного катета и прилежащего (в уравнении нужно поделить одно на другое). Если речь идет о числах, тупых, развернутых углов и углов, превышающих 360 градусов, то тангенс определяется при помощи синуса и косинуса (посредством их отношения и деления).
Теорема синусов и косинусов используется для того чтобы искать элементы в произвольном треугольнике. Такой поиск используется часто.
Угол поворота
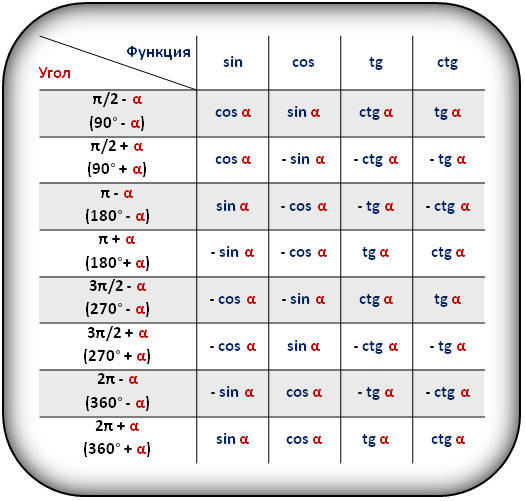
Определения, данные выше, относятся к острым углам. В тригонометрии вводится понятие угла поворота, величина которого, в отличие от острого угла, не ограничена рамками от 0 до 90 градусов.Угол поворота в градусах или радианах выражается любым действительным числом от -∞ до +∞.
В данном контексте можно дать определение синуса, косинуса, тангенса и котангенса угла произвольной величины. Представим единичную окружность (круг) с центром в начале декартовой системы координат.
Начальная точка A с координатами (1, 0) поворачивается вокруг центра единичной окружности на некоторый угол α и переходит в точку A1. Определение дается через координаты точки A1(x , y).
Синус угла поворота α — это ордината точки A1(x , y). sin α=y
Косинус угла поворота α — это абсцисса точки A1(x , y). cos α=икс
Тангенс угла поворота α — это отношение ординаты точки A1(x , y) к ее абсциссе. tg α=yx
Котанг угла поворота α — это отношение абсциссы точки A1(x , y) к ее ординате. ctg α=xy
Синус и косинус определены для любого угла поворота. Это логично, ведь абсциссу и ординату точки после поворота можно определить при любом угле. Иначе обстоит дело с тангенсом и котангенсом. Тангенс не определен, когда точка после поворота переходит в точку с нулевой абсциссой (0, 1) и (0, -1). В таких случаях выражение для тангенса tg α=yx просто не имеет смысла, так как в нем присутствует деление на ноль. Аналогична ситуация с котангенсом. Отличие состоит в том, что котангенс не определен в тех случаях, когда в ноль обращается ордината точки.
Простое правило: синус и косинус определены для любых углов α.
Тангенс определен для всех углов, кроме α=90°+180°·k, k∈Z (α=π2+π·k, k∈Z)
Котангенс определен для всех углов, кроме α=180°·k, k∈Z (α=π·k, k∈Z)
При решении практических примеров не говорят «синус угла поворота α». Слова «угол поворота» просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь.
Числа
Как быть с определением синуса, косинуса, тангенса и котангенса числа, а не угла поворота?
Синусом, косинусом, тангенсом и котангенсом числа t называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в t радиан.
Например, синус числа 10π равен синусу угла поворота величиной 10π рад.
Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Рассмотрим его подробнее.
Любому действительному числу t ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат. Синус, косинус, тангенс и котангенс определяются через координаты этой точки.
Начальная точка на окружности — точка A c координатами (1, 0).
Положительному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t.
Отрицательному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t.
Теперь, когда связь числа и точки на окружности установлена, переходим к определению синуса, косинуса, тангенса и котангенса.
Синус числа t — ордината точки единичной окружности, соответствующей числу t. sin t=y
Косинус числа t — абсцисса точки единичной окружности, соответствующей числу t. cos t=x
Тангенс числа t — отношение ординаты к абсциссе точки единичной окружности, соответствующей числу t. tg t=yx=sin tcos t
Последние определения находятся в соответствии и не противоречат определению, данному в начале это пункта. Точка на окружности, соответствующая числу t, совпадает с точкой, в которую переходит начальная точка после поворота на угол t радиан.
Тригонометрические функции углового и числового аргумента
Каждому значению угла α соответствует определенное значение синуса и косинуса этого угла. Также, как всем углам α, отличным от α = 90 ° + 180 ° · k , k ∈ Z ( α = π 2 + π · k , k ∈ Z ) соответствует определенное значение тангенса. Котангенс, как сказано выше, определен для всех α, кроме α = 180 ° · k , k ∈ Z ( α = π · k , k ∈ Z ).
Можно сказать, что sin α, cos α, tg α, ctg α — это функции угла альфа, или функции углового аргумента.
Аналогично можно говорить о синусе, косинусе, тангенсе и котангенсе, как о функциях числового аргумента. Каждому действительному числу t соответствует определенное значение синуса или косинуса числа t. Всем числам, отличным от π 2 + π · k , k ∈ Z соответствует значение тангенса. Котангенс, аналогично, определен для всех чисел, кроме π · k , k ∈ Z.
Синус, косинус, тангенс и котангенс — основные тригонометрические функции.
Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело.
Связь определений sin, cos, tg и ctg из геометрии и тригонометрии
Вернемся к данным в самом начале определениям и углу альфа, лежащему в пределах от 0 до 90 градусов. Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью соотношений сторон прямоугольного треугольника. Покажем это.
Возьмем единичную окружность с центром в прямоугольной декартовой системе координат. Повернем начальную точку A(1,0) на угол величиной до 90 градусов и проведем из полученной точки A1(x,y) перпендикуляр к оси абсцисс. В полученном прямоугольном треугольнике угол A1OH равен углу поворота α, длина катета OH равна абсциссе точки A1(x,y). Длина катета, противолежащего углу, равна ординате точки A1(x,y), а длина гипотенузы равна единице, так как она является радиусом единичной окружности.
В соответствии с определением из геометрии, синус угла α равен отношению противолежащего катета к гипотенузе.
sin α=A1HOA1=y1=y
Значит, определение синуса острого угла в прямоугольном треугольнике через соотношение сторон эквивалентно определению синуса угла поворота α, при альфа лежащем в пределах от 0 до 90 градусов.
Аналогично соответствие определений можно показать для косинуса, тангенса и котангенса.
Синус, косинус, тангенс и котангенс: основные формулы
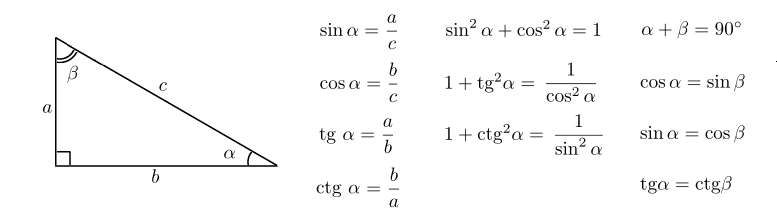
- Определение
- График синуса
-
Свойства синуса
- Обратная к синусу функция
- Таблица синусов
Определение
Синус острого угла α (sin α) – это отношение противолежащего катета (a) к гипотенузе (c) в прямоугольном треугольнике.
sin α = a / c
Например:
a = 3
c = 5
sin α = a / c = 3 / 5 = 0.6
График синуса
Функция синуса пишется как y = sin (x). График называется синусоидой и в общем виде выглядит следующим образом:
Синусоида – это периодическая функция с периодом T = 2π.
Свойства синуса
Ниже в табличном виде представлены основные свойства синуса с формулами:
Обратная к синусу функция
Арксинус x – это обратная функция к синусу x, при -1≤x≤1.
Если синус угла у равняется х (sin y = x), значит арксинус x равен у:
arcsin x = sin-1 x = y
Таблица синусов
| x (°) | x (рад) | sin x |
| -90° | -π/2 | -1 |
| -60° | -π/3 | -√3/2 |
| -45° | -π/4 | -√2/2 |
| -30° | -π/6 | -1/2 |
| 0° | 0 | 0 |
| 30° | π/6 | 1/2 |
| 45° | π/4 | √2/2 |
| 60° | π/3 | √3/2 |
| 90° | π/2 | 1 |
microexcel.ru
Тригонометрия — это раздел математики, в котором изучаются тригонометрические функции, их свойства, взаимосвязи и применение.
Слово «тригонометрия» образовано от греческих слов «trigonom» (треугольник) и «metreo» (измерять).
Возникновение и развитие тригонометрии связаны с практическими потребностями в измерении и вычислении сначала элементов треугольников на местности, а позднее — в строительстве, мореплавании и астрономии. Современная тригонометрия широко применяется в разных областях математики, в частности в геометрии, других науках, в технике. Например, тригонометрические функции используются при решении задач оптики, задач кинематического анализа и синтеза механизмов, гармонического анализа и других.
Cинус, косинус, тангенс, котангенс острого угла прямоугольного треугольника
Нет понятий «просто синус» или «просто косинус», не имеют смысла записи типа «sin» и «cos» сами по себе, они сами по себе никакой величины не обозначают (точно так же, как и, например, значок квадратного корня сам по себе). Те, кто этого не понимает, часто делает грубую ошибку типа: sin x /cos x = in /co
Есть понятие синуса, косинуса, тангенса, котангенса как тригонометрических функций угла. Здесь угол — аргумент функции. Он может обозначаться «х», «а», «альфа», «бета», «гамма», «фи», «дельта» или ещё какой-нибудь буквой. Суть от этого не меняется.
Для того, чтобы более наглядно представить приведенные ниже определения, начертите прямоугольный треугольник. Это треугольник, один из углов которого — прямой (т.е. один из углов равен 90 градусов). Стороны, прилежащие к прямому углу (перпендикулярные друг другу стороны) — это катеты данного прямоугольного треугольника. Противолежащая прямому углу сторона — это гипотенуза.
Теперь выберите любой из двух других (острых) углов треугольника и обозначьте его, например, альфа. Один из катетов будет примыкать к вершине этого угла (и, собственно, образовывать этот угол вместе с гипотенузой). Это — прилежащий катет. Другой катет не примыкает к вершине этого угла, он находится как бы напротив данной вершины. Это — противолежащий катет.
Кстати, почему-то не все представляют, что такое угол треугольника при данной вершине. У треугольника (обозначим его ABC) есть три вершины: А, В и С. Когда говорят об угле А треугольника, то подразумевают угол, образованный сторонами ВА и АС. Это и есть угол при вершине А.
Итак,
Синусом острого угла называется отношение противолежащего этому углу катета к гипотенузе.
Косинусом острого угла называется отношение прилежащего к этому углу катета к гипотенузе.
Тангенсом острого угла называется отношение противолежащего этому углу катета к прилежащему катету.
Котангенсом острого угла называется отношение прилежащего этому углу катета к противолежащему катету.
Секансом острого угла называется отношение гипотенузы к прилежащему к этому углу катету. Обозначается: sec x.
Косекансом острого угла называется отношение гипотенузы к противолежащему этому углу катету. Обозначается: cosec x.
Как найти углы в прямоугольном треугольнике, если известны стороны?
Дан треугольник АВС, угол С — прямой.
Стороны АВ, АС и ВС известны.
Т.к. угол С — прямой, он равен 90 градусам.
Другие углы можно найти, например, так:
если известен катет и гипотенуза
sinA = BC / AB,
sinB = AC / AB,
если известны два катета
tg A = BC / AC
tg B = AC / BC
Предположим, получили, что sin A = ½. По таблице смотрим, что такому значению sin x соответствует величина угла 30 градусов.
Или, к примеру, получили, что tg B = 1. Значит, угол В равен 45 градусов.
Или, к примеру, мы получили, что sin B = 0,259. По таблице Брадиса или с помощью калькулятора находим, что угол В равен 15 градусов.
sin 15° = 0,259
arcsin0,259 = 15°
Как найти углы в прямоугольном треугольнике, если известен один угол?
Поскольку треугольник прямоугольный, то один из его углов равен 90 градусов. Величина второго угла известна (по условию задачи, обозначим её альфа). В сумме углы треугольника составляют 180 градусов. Значит, третий угол равен 180—90—альфа.
Еединичная окружность (единичный круг)
Единичный круг — это круг с центром в начале координат и радиусом, равным единице (R = 1).
Единичная окружность — это окружность единичного круга (т.е. окружность с центром в начале координат и с радиусом, равным единице).
Единичный радиус-вектор — это вектор, начало которого совпадает с началом координат, а его длина равна единице.
Углы отсчитывают от начального положения подвижного радиуса-вектора (совпадает с положением Ох).
Координатные четверти отсчитываются так:
y
|
|
(II четверть) | (I четверть)
|
________________________ x
|0
|
(III четверть) | (IV четверть)
|
|
Угол первой четверти — от 0 до 90 градусов (от 0 до пи/2).
Угол второй четверти — от 90 до 180 градусов (от пи/2 до пи).
Угол третьей четверти — от 180 до 270 градусов (от пи до 2пи/3).
Угол четвертой четверти — от 270 до 360 градусов (от 2пи/3 до 2пи).
Например:
- углы первой четверти: 30 градусов, 85 градусов, пи/4;
- углы второй четверти: 120 градусов, 178 градусов;
- углы третьей четверти: 205 градусов, 260 градусов;
- углы четвертой четверти: 272 градуса, 305 градусов.
Тригонометрические функции
К тригонометрическим функциям относятся функции:
y = sin x;
y = cos x;
y = tg x;
y = ctg x;
y = sec x;
y = cosec x.
Синусом угла, образованного осью Ох и произвольным радиусом-вектором ОА, называется отношение проекции этого вектора на ось Оу к его длине.
Косинусом угла, образованного осью Ох и произвольным радиусом-вектором ОА, называется отношение проекции этого вектора на ось Ох к его длине.
Тангенсом угла, образованного осью Ох и произвольным радиусом-вектором ОА, называется отношение проекции этого вектора на ось Оу к его проекции на ось Ох.
Котангенсом угла, образованного осью Ох и произвольным радиусом-вектором ОА, называется отношение проекции этого вектора на ось Ох к его проекции на ось Оу.
Секансом угла, образованного осью Ох и произвольным радиусом-вектором ОА, называется отношение длины этого вектора к его проекции на ось Ох.
Косекансом угла, образованного осью Ох и произвольным радиусом-вектором ОА, называется отношение длины этого вектора к его проекции на ось Оу.
Тригонометрические функции связаны между собой, и этим можно воспользоваться для нахождения синуса угла по его косинусу или котангенсу или косинуса угла по его синусу или тангенсу.
Как найти синус угла, если известен косинус?
Нужно воспользоваться основным тригонометрическим тождеством:
sin2a + cos2a = 1
sin2a = 1 − cos2a
|sin a| = КОРЕНЬ(1 − cos2a)
sin a = ± КОРЕНЬ(1 − cos2a)
знак перед корнем нужно выбрать в соответствии с четвертью данного угла (синус положительный в I и II четвертях, косинус положительный в I и IV четвертях)
Как найти косинус угла, если известен синус?
Нужно воспользоваться основным тригонометрическим тождеством:
sin2a + cos2a = 1
cos2a = 1 − sin2a
|cos a| = КОРЕНЬ(1 − sin2a)
cos a = ± КОРЕНЬ(1 − sin2a)
знак перед корнем нужно выбрать в соответствии с четвертью данного угла (синус положительный в I и II четвертях, косинус положительный в I и IV четвертях)
Как найти синус угла, если известен котангенс?
Нужно воспользоваться тригонометрическим тождеством
1 + ctg2 a = 1/sin2 a
sin2 a = 1 / (1 + ctg2 a)
|sin a| = 1/ КОРЕНЬ(1 + ctg2 a)
sin a = ±1/ КОРЕНЬ(1 + ctg2 a)
знак перед корнем нужно выбрать в соответствии с четвертью данного угла (синус положительный в I и II четвертях, котангенс положительный в I и III четвертях)
Как найти косинус угла, если известен тангенс?
Нужно воспользоваться тригонометрическим тождеством
1 + tg2 a = 1/cos2 a
cos2 a = 1 / (1 + tg2 a)
|cos a| = 1/ КОРЕНЬ(1 + tg2 a)
cos a = ±1/ КОРЕНЬ(1 + tg2 a)
знак перед корнем нужно выбрать в соответствии с четвертью данного угла (косинус положительный в I и IV четвертях, тангенс положительный в I и III четвертях)
Тригонометрическое тождество
Тригонометрическим тождеством называется равенство, в которое входят тригонометрические функции и которое удовлетворяется произвольным допустимым значением угла — аргумента тригонометрических функций, но не удовлетворяется, если каждую в отдельности тригонометрическую функцию заменить произвольной величиной.
Основные тригонометрические тождества:
sin2a + cos2a = 1
tg a = sin a / cos a
ctg a = cos a / sin a
sec a = 1 / cos a
cosec a = 1 / sin a
Arcsin, arcos, arctg, arcctg (обратные тригонометрические функции)
- arcsin — читается: арксинус;
- arcos — читается: арккосинус;
- arctg — читается: арктангенс;
- arcctg — читается: арккотангенс.
arcsin, arcos, arctg, arcctg — это обратные тригонометрические функции.
Обратной тригонометрической функцией y = arcsin x называют угол у, взятый на отрезке от –пи/2 до +пи/2, синус которого равен х:
y = arcsin x sin y = x
Обратной тригонометрической функцией y = arccos x называют угол у, взятый на отрезке от –пи до +пи, косинус которого равен х:
y = arccos x cos y = x
Обратной тригонометрической функцией y = arctg x называют угол у, взятый на промежутке от –пи/2 до +пи/2 (исключая концы), тангенс которого равен х:
y = arctg x tg y = x
Обратной тригонометрической функцией y = arcctg x называют угол у, взятый на промежутке от 0 до пи (исключая концы), котангенс которого равен х:
y = arctg x tg y = x
Например,
sin 30° = 0,5
arcsin0,5 = 30°
Синусоида и косинусоида
График функции y = sin x называется синусоидой.
График функции y = cos x называется косинусоидой.
Источники информации:
- Справочник по элементарной математике. Геометрия, тригонометрия, векторная алгебра. Под редакцией П.Ф. Фильчакова. —К.: Наукова думка, 1967. — 442 с.
- В.Д. Гетманцев, О.Ф. Саушкiн. Математика: Тригонометрiя: Посiбник для слухачiв пiдотовчих вiддiлень, вступникiв до вищих навчальних закладiв, студентiв педагогiчних iнститутiв (на укр.). —К.: Либiдь, 1994. — 144 с.
- docme.ru — зачем нужна тригонометрия?
- ru.wikipedia.org — Википедия — тригонометрия;
- ru.wikihow.com — как изучать тригонометрию?
Итак, в прошлый раз мы с вами успешно познакомились с тригонометрическими функциями — синусом, косинусом, тангенсом и котангенсом. И чётко уяснили себе следующее:
1. Синус, косинус, тангенс и котангенс — это просто какие-то безразмерные числа. Отношения сторон в прямоугольном треугольнике. Для каждого конкретного угла — свои.
2. Тригонометрические функции крепко-накрепко связаны с углом. Знаем угол — знаем и все его тригонометрические функции. И наоборот.
Если не уяснили эти простые вещи, то добро пожаловать по ссылочке, пока не поздно. А мы продолжаем.
То, что между этой великолепной четвёркой существует тесная связь, не вызывает никаких сомнений. Всякая связь в математике задаётся, чаще всего, формулами. В тригонометрии формул — огромное количество. Это и формулы приведения, и формулы сложения, двойного угла, понижения степени и многие-многие другие.
В этом же уроке мы рассмотрим лишь самые главные из них. Они так и называются — основными тригонометрическими формулами. Их всего шесть.
Вот они:
Здесь «альфа» — какой-то угол.
Эти шесть формул — краеугольный камень всей тригонометрии. То, чего не знать нельзя. Если вы не знаете, чему равен, скажем, косинус тройного угла — не проблема. Никто вас не осудит. Но если вы не знаете, что sin2x+cos2x = 1, то будьте готовы получить заслуженную двойку. Вот так вот.
Сразу предупреждаю, что три последних формулы (4-6) очень часто выпадают из памяти. Почему-то… Можно, конечно, легко вывести эти формулы из первых трёх, но в тревожной боевой обстановке ЕГЭ, когда на карту поставлена ваша дальнейшая судьба… сами понимаете.) Но не переживайте, совсем скоро я вам покажу простой и наглядный способ вывести все эти формулы просто и безошибочно!
Из этих формул сразу видно, что они неразрывно связывают между собой синус, косинус, тангенс и котангенс одного и того же угла. Именно эти формулы нам позволяют находить все тригонометрические функции одного и того же угла, если известна хотя бы одна из них. Причём (важно!) не находя сам угол! Такие задания очень популярны как сами по себе, так и могут быть промежуточным этапом в более серьёзных заданиях. В тригонометрических уравнениях, к примеру. И особенно в высшей математике, в тех же пределах, интегралах, дифференциальных уравнениях и прочих крутых темах.
Кстати говоря, хочу обратить ваше внимание на один частый ляп в неправильном написании тригонометрических функций в степенях — в квадрате, в кубе и так далее.
Например, выражение квадрат синуса (или синус в квадрате) в тригонометрии пишется вот так:
sin2x
Двойка (т.е. степень) в этом случае пишется между углом и названием функции. Эта запись как раз и говорит нам о том, что в квадрат возводится именно сама функция (т.е. в нашем случае — синус).
А вот запись
sin x2
будет говорить уже о том, что в квадрат возводится, не синус угла, а только сам угол! Почувствуйте разницу, что называется.)
Во избежание путаницы, ещё раз (и навсегда!) всё то же самое, но со скобочками:
sin2x = (sin x)2
sin x2 = sin(x2)
Конечно, заниматься возведением углов в квадрат мы в школьной тригонометрии вряд ли будем. За ненадобностью.) Зато возведением функций в квадрат — постоянно. Так что привыкаем, не путаемся и пишем правильно.
Ну что, посмотрим на вывод основных формул? Чтобы всё встало на свои места. Зачем и почему? Да потому, что любая формула запоминается гораздо проще, если есть возможность её «пощупать» в реале, а не механически зазубривать и бездумно принимать на веру, как само собой разумеющееся.) Тем более что это не просто, а очень просто!
Вывод и смысл основных тригонометрических формул.
Первым делом, я снова нарисую наш старый добрый прямоугольный треугольник. Не обязательно по линеечке, по клеточкам, а просто схематично. От руки.
Как-то вот так:
Что нам понадобится ещё для дальнейшей работы?
1. Теорема Пифагора:
a2 + b2 = c2
2. Определения тригонометрических функций:
sin α = a/c
cos α = b/c
tg α = a/b
ctg α = b/a
3. Тождественные преобразования уравнений.
Всё. Вот и все инструменты.
А вот теперь начинается самое весёлое. Сейчас я беру нашу горячо любимую теорему Пифагора a2 + b2 = c2 и… начинаю всячески над ней издеваться, подвергая её всевозможным пыткам.) Результатами пыток станут целых три формулы из нашего списка!
Итак, пытка №1. Берём теорему Пифагора
a2 + b2 = c2
и делим обе части на квадрат гипотенузы. На с2. А чего? Имеем полное право! Любая формула — это тоже уравнение! И к любой формуле применимы все те же тождественные преобразования (перенос вправо/влево, умножение/деление), которые мы проделываем для «обычных» уравнений с иксом.
Что получим:
А вот теперь соображаем, уже из тригонометрии, что же такое a/c? Правильно, синус альфа! Противолежащий катет (a) к гипотенузе (c). А b/c? Косинус альфа! А дробь с2/с2 — это… это… единичка! Как и любое число, делённое само на себя, да. Элементарно, Ватсон!)
Так у нас с вами рождается на свет формула №1:
Эта формула — самая популярная во всей тригонометрии! По-другому её ещё называют основным тригонометрическим тождеством.
Она же, но записанная слегка по-другому (в зависимости от того, что именно надо выразить):
sin2α = 1 — cos2α
cos2α = 1 — sin2α
Эти две модификации формулы №1 весьма и весьма часто применяются в примерах по тригонометрии! Именно они позволяют легко перевращать синусы в косинусы (и наоборот). Имеет смысл запомнить.
А теперь продолжаем мучить теорему Пифагора дальше.) А что если в этот раз поделить обе части не на c2, а, скажем, на b2? Ну разве b2 чем-то хуже?!
Давайте поделим и посмотрим:
И снова соображаем из тригонометрии (и нашего рисунка), что же такое a/b. Верно, тангенс альфа! А c/b? Так сразу и не скажешь… Стоп! Но ведь что такое b/c — это же нам ясно! Это косинус альфа! У нас же в формуле стоит тот же косинус, только перевёрнутый вверх ногами — c/b. Значит, справа в скобках у нас стоит величина, обратная косинусу: 1/cos α.
Итого имеем следующее:
Переписываем в привычном виде и рождаем формулу №5:
А если поделить всё на a2? Верно! Получится шестая формула!
Попробуйте получить самостоятельно, очень полезно.)
Вторая, третья и четвёртая формулы выводятся совсем элементарно, исходя только из определения тригонометрических функций и элементарных действий с дробями. Теорема Пифагора здесь не нужна.
Что, например, у нас получится, если мы просто поделим синус на косинус?
Делим и получаем:
И все дела.) С котангенсом — аналогично.
А если перемножить тангенс и котангенс? Ну-ка, ну-ка…
Вот и вся премудрость. Убедились, насколько всё просто?)
Решение простейших заданий по тригонометрии.
Теория теорией, но нам ведь опыт наращивать надо, верно? Так что пора приступать к задачкам. Всё как всегда — от совсем простых и безобидных до вполне себе серьёзных.
Ну что, приступим? 
1. Вычислить значение tg x, если ctg x = 1,25.
Здесь, ясное дело, надо искать формулу, связывающую тангенс и котангенс. Это четвёртая формула. Самое главное — сообразить, что вместо «альфа» можно писать любую другую букву. Лишь бы везде одна и та же была. Для нашего задания будет:
tg x · ctg x = 1
Можно прямо в эту формулу подставить значение ctg x = 1,25:
tg x · 1,25 = 1
Осталось лишь решить это простенькое уравнение. Да-да. Ещё раз подчёркиваю, что любая формула, любое соотношение, соединённое знаком равенства («=»), — это всегда уравнение! А там, где уравнение, там автоматически и тождественные преобразования уравнений, да…
Наше соотношение — это тоже уравнение. Где роль неизвестного играет tg x. Прошу заметить, не икс, а именно весь тангенс целиком! Вас же не смущает уравнение, скажем, y·1,25 = 1? Что вы обычно делаете в таких случаях? Правильно, делите обе части на 1,25, чтобы слева остался чистый игрек. Вот и здесь тоже делим обе части на 1,25, добиваясь слева чистого тангенса.
Делим и получаем:
tg x = 0,8
И все дела. Это и есть верный ответ.
Можно поступить иначе. Сначала выразить из общей формулы тангенс:
tg x = 1/ctg x
А уже теперь подставить вместо ctg x его значение 1,25. Получим то же самое. И так и эдак можно. Разницы — никакой. Но… если осознать смысл этой формулы поглубже, то можно получить очень простой и очень полезный практический приём.
Запоминаем:
Если единицу разделить на котангенс, то получим тангенс. И наоборот, единица, делённая на тангенс, даёт котангенс. Эти две функции взаимно обратны!
Что? Не знаете, как разделить единичку на число? Ну, это вопрос не к тригонометрии. Вопрос к шестому классу, к дробям… Как разделить? Да просто перевернуть это самое число и все дела!
Например:
— если tg x = 3/4, то ctg x = 4/3;
— если ctg x = 2, то tg x = 1/2;
— если tg x = 0,7 = 7/10, то ctg x = 10/7;
— если ctg x = 0,25 = 1/4, то tg x = 4.
И так далее и тому подобное. В общем, вы поняли…)
Продолжаем развлекаться?)
Например, классика жанра:
2. Известно, что β — острый угол в прямоугольном треугольнике.
Найти sinβ, если cosβ = 0,6.
Ищем формулу, связывающую синус и косинус. Это самая первая формула:
sin2β+cos2β = 1
Подставляем в неё известную нам величину 0,6 вместо косинуса:
sin2β+0,62 = 1
И считаем, как обычно:
sin2β+0,36 = 1
sin2β = 1 — 0,36
sin2β = 0,64
Вот, практически, и всё. У нас есть квадрат синуса. А нужен сам синус. Для этого осталось всего лишь извлечь корень и — ответ готов! Корень из 0,64 будет 0,8.
sinβ = 0,8
Задачка почти элементарная. Но словечко «почти» я здесь употребил не случайно. Почему? Дело всё в том, что ответ -0,8 тоже вполне себе подходит: (-0,8)2 тоже будет 0,64.
Два разных ответа получается. А нужен один. Второй — неправильный. Что делать? Да всё как обычно! Внимательно прочитать задание! Там зачем-то сказано: «… если β — острый угол…» А лишних слов в заданиях, как правило, не бывает, да… Именно эти слова — и есть дополнительная информация к решению.
Что такое острый угол? Это угол меньше 90 градусов. А у таких углов все тригонометрические функции (в том числе и синус, да…) всегда положительные. То есть, отрицательный ответ мы здесь просто отбрасываем. Имеем полное право.
Ответ: sinβ = 0,8
Собственно, на данном этапе нам такие тонкости особо не нужны. Пока… Ибо сейчас мы работаем только с прямоугольными треугольниками, где углы могут быть только острые. И не знаем, счастливые, что бывают и отрицательные углы, и углы в 1000 градусов… И у всех этих жутких углов тоже есть свои тригонометрические функции! С плюсом и с минусом. Всё от конкретного угла зависит.
А вот старшеклассникам без учёта знака — никак. К сожалению… Но не будем бежать впереди паровоза. Всему своё время.)
Решаем следующую задачку. Покруче.
Определить косинус острого угла β в прямоугольном треугольнике, если ctgβ = 4/3.
На первый взгляд, всё просто. Но попробуем найти в нашем списке формулу, связывающую котангенс и косинус. Ищем и… Вы правы! Такой формулы нету.) Надо как-то выкручиваться…
Можно работать с шестой формулой:
Подставим в эту формулу значение котангенса и преобразуем:
Выразим из этой пропорции (т.е. тоже уравнения!) квадрат синуса:
sin2β = 9/25
Итак, квадрат синуса у нас есть. Теперь его легко можно превратить в квадрат косинуса по первой формуле:
cos2β = 1 — sin2β
Извлекаем корень и определяем сам косинус:
Читаем ещё раз задание и вспоминаем, что у острого угла все тригонометрические функции всегда положительны. Отбрасываем отрицательное значение и получаем окончательный ответ:
cosβ = 4/5
Это был один способ. Можно решать и по-другому, через пятую формулу:
Для этого нам надо:
1) Превратить котангенс в тангенс по формуле №4;
2) Подставить значение тангенса в формулу;
3) Преобразовать выражение и выразить из него квадрат косинуса;
4) Извлечь корень и получить два значения косинуса;
5) Сообразить (из условия задания), что в прямоугольном треугольнике все тригонометрические функции всегда положительны. Отбросить отрицательный ответ и получить косинус.
Как видим, хрен редьки не слаще, да.) Но это ещё не всё. Для такого решения надо ещё вспомнить эти формулы! А если забыли? Собственно, в этом-то и кроется главная проблема в их применении. Да ещё и куча вычислений… В общем, не подарок…
Без паники! Для таких задачек есть очень простой и, главное, наглядный способ решения! Геометрический.) Читаем, вникаем и запоминаем.
Итак, нам дано: ctgβ = 4/3.
Нарисуем этот котангенс!
Да-да! Схематично. Как? Очень просто! Берём черновик и рисуем любой прямоугольный треугольник. Кривовато, от руки, даже не соблюдая пропорций. У нас не ИЗО и не черчение с вами.) Выбираем любой острый угол и обозначаем его «бета».
Вот так:
Вспоминаем теперь, что котангенс — это отношение прилежащего катета к противолежащему. И ставим на соответствующих катетах их длины. Какие? А какие в нашем котангенсе записаны! 4 и 3. Противолежащий катет a = 3, а прилежащий b = 4.
Кстати, прошу заметить, что реальные размеры треугольника нас совершенно не интересуют! Мы говорим сами себе: «Допустим, прилежащий к углу катет будет 4, а противолежащий — 3″. Тогда котангенс нашего угла β будет как раз 4/3, как и в задании.
Чего ещё нам не хватает для полного счастья? Гипотенузы нам не хватает! Не беда: Пифагор ещё никого не подводил.)
Считаем:
c2 = a2 + b2
c2 = 42 + 32 = 25
c = 5
Итак, гипотенуза равна пяти. Подписываем на картинке.)
А теперь считаем косинус прямо по заклинанию: отношение прилежащего катета к гипотенузе.
cosβ = b/c = 4/5
Всё! Быстро, правда?) Вот такой красивый графический способ-лайт. Безо всяких формул.) Ну… почти. Ведь теорему Пифагора всяко надо знать, да.)
Следующее задание.
Упростите выражение:
Что, внушает? В таких замороченных примерах необходимо понимать, что синусы и косинусы никоим образом не отменяют всей остальной математики. И подчиняются тем же самым общим правилам, что и обычные числа и буквы в алгебре! А именно — разложение на множители, формулы сокращённого умножения, раскрытие скобок, приведение подобных, сокращение дробей и т.п.
Вас же никак не смущает дробь
правда ведь? Хотя кого-то она, возможно, тоже смущает, да…
Естественно, к основным правилам алгебры добавляется ещё и специфика самой тригонометрии, от этого никуда не денешься. Собственно, с этой целью и разбираем соответствующий пример, да.)
Начнём с числителя нашей здоровенной дроби. Забудем на минутку про тригонометрию и прикинем, что там можно сделать, основываясь на обычных правилах алгебры. Да хотя бы вынести один синус за скобки! Верно, давайте вынесем:
sin3x·cos x + sin x·cos3x = sin x (sin2x·cos x+cos3x)
Ой, ещё и косинус вынести можно!
sin x (sin2x·cos x+cos3x) = sin x·cos x (sin2x+cos2x)
Вот так. Самые грамотные вообще сразу целиком вынесут произведение sin x·cos x за скобку. Знания и наблюдательность иногда очень помогают. Если они есть.)
А вот теперь и тригонометрия в дело вступает! Что у нас в скобочках? Да! В скобочках у нас — чистая формула №1. Или основное тригонометрическое тождество:
sin2x+cos2x = 1
От умножения на единичку выражение не меняется. Значит, числитель нашей дроби будет не что иное, как просто sin x·cos x.
Всё. Числитель упростили до упора. Работаем со знаменателем:
(1–sin x)(1+sin x)
А здесь что? Разность ква… Точно! Разность квадратов! Такая родная и знакомая формула:
(a—b)(a+b) = a2 — b2
Под буквой «a» здесь скрывается единичка, а под буквой «b» — выражение sin x. Ну и что? Важно понимать, что под буквами в алгебраических выражениях может скрываться всё что угодно! И числа, и синусы, и логарифмы, и степени — любые сложные выражения! Алгебре все выражения по плечу. Иначе она не была бы алгеброй, да…)
Вот и срабатываем прямо по формуле разности квадратов:
(1–sin x)(1+sin x) = 12 — (sin x)2 = 1 — sin2x
А вот теперь соображаем, уже из тригонометрии, что
1 — sin2x = cos2x
Вставляем упрощённые числитель и знаменатель в нашу дробь, сокращаем что сокращается и получаем:
Казалось бы, всё. В рамках алгебры 7-го класса такая дробь дальнейшему упрощению уже не поддаётся, но алгебра в этом примере и так постаралась на славу. Зато в рамках тригонометрии эта дробь вполне себе упрощается! Что же такое синус поделить на косинус? Тангенс, конечно же! Чистая формула №2.
Вот теперь всё. Значит, окончательный результат упрощения вот такой:
Эффект потрясающий, правда?
Запоминаем:
В тригонометрии очень популярны задания, где надо использовать алгебру 7-го класса. А именно — разложение на множители, формулы сокращённого умножения, раскрытие скобок, приведение подобных, сокращение дробей и т.п. Проверяем замороченные примеры на алгебру 7-го класса!
Ещё из той же оперы:
Докажите тождество:
Напоминаю, что страшная фраза «доказать тождество» всего лишь означает, что надо упростить обе части предлагаемого равенства (или какую-то одну, более сложную) и убедиться, что слева и справа стоит одно и то же выражение.
Вот и пробуем добраться до одинакового выражения! Начинаем с левой части. Превращаем тангенс в отношение синуса к косинусу по второй формуле:
Выражение в скобках превращаем в квадрат косинуса по первой формуле:
Подставляем, сокращаем косинусы и получаем:
Ну вот. Левая часть упрощена по максимуму. С правой частью аналогично — формулы №1 и №3 нам в помощь:
Вот и всё! Слева и справа мы получили совершенно одинаковые выражения! А именно — sinα·cosα. Что и требовалось доказать.)
Итак, самое главное.
Чётко уясняем: тригонометрические функции (синус, косинус, тангенс и котангенс) одного угла неразрывно связаны между собой основными тригонометрическими формулами. Если нам известна хотя бы одна из функций — значит, можно (при наличии необходимой дополнительной информации) вычислить и все остальные!
А теперь порешаем, как обычно.
Простенькие задачки:
1. Косинус острого угла равен 7/25. Найдите синус этого угла.
2. Известно, что β — угол в прямоугольном треугольнике. Найти tgβ, если sinβ = 15/17.
3. Найдите косинус острого угла A, если известно, что ctg A = 2,4.
Покруче:
4. Найдите значение выражения 4cos213° — 4 + 4sin213°.
5. Упростите выражение и найдите его значение, если sinβ = 1:
И совсем круто:
6. Известно, что tg y = 3. Найдите значение выражения:
Что, страшно? Мы такого не решали? Да, не решали. Но и самим поразмышлять тоже иногда полезно, да.) Подсказка: основное свойство дроби вам в помощь! Ну и формула №2 для тангенса, само собой.)
Ответы (в традиционном беспорядке):
тригонометрическая функция угла
| Синус | |
|---|---|
 |
|
| Основные характеристики | |
| Четность | нечетное |
| Домен | (- ∞, + ∞) |
| Кодомен | [−1, 1] |
| Период | 2π |
| Конкретные значения | |
| В нуле | 0 |
| Максимум | (2kπ + π / 2, 1) |
| Минимум | (2kπ — π / 2, −1) |
| Особенности | |
| Корень | kπ |
| Критическая точка | kπ + π / 2 |
| Перегиб точка | kπ |
| Фиксированная точка | 0 |
|
В математике синус — это тригонометрическая функция угла угла. Синус острого угла определяется в контексте прямоугольного треугольника : для указанного угла это отношение длины стороны, противоположной этому углу, к длине самой длинной стороны. треугольника (гипотенуза ). Для угла x { displaystyle x}

В более общем смысле определение синуса ( и другие тригонометрические функции) могут быть расширены до любого действительного значения с точки зрения длины определенного линейного сегмента в единичной окружности . Более современные определения выражают синус как бесконечный ряд или как решение некоторых дифференциальных уравнений, что позволяет их расширить до произвольных положительных и отрицательных значений и даже до комплексных чисел.
Синусоидальная функция обычно используется для моделирования периодических явлений, таких как звук и световые волны, положение и скорость гармонических осцилляторов, интенсивность солнечного света и продолжительность светового дня, а также изменения средней температуры на всем протяжении год.
Функциональный синус можно проследить до функций jyā и koṭi-jyā, используемых в период Гупта Индийская астрономия (Aryabhatiya, Сурья Сиддханта ), путем перевода с санскрита на арабский, а затем с арабского на латинский. Слово «синус» (латинское «синус») произошло от латинского неправильного перевода Робертом Честерским арабского джиба, который является транслитерацией санскрита. слово для половины хорды, джья-ардха.
Содержание
- 1 Определение прямоугольного треугольника
- 2 Определение единичного круга
- 3 Тождества
- 3.1 Взаимное
- 3.2 Обратное
- 3.3 Исчисление
- 3.4 Другие тригонометрические функции
- 3.5 Функция квадрата синуса
- 4 Свойства, относящиеся к квадрантам
- 5 Определение ряда
- 5.1 Непрерывная дробь
- 6 Фиксированная точка
- 7 Длина дуги
- 8 Закон синусов
- 9 Особые значения
- 10 Связь с комплексными числами
- 10.1 Синус с комплексным аргументом
- 10.1.1 Разложение комплексного синуса на частичную дробь и произведение
- 10.1.2 Использование комплексного sine
- 10.2 Сложные графы
- 10.1 Синус с комплексным аргументом
- 11 История
- 11.1 Этимология
- 12 Программные реализации
- 12.1 Реализации на основе поворотов
- 13 См. также
- 14 Цитаты
- 15 Ссылки
- 16 Внешние ссылки
прямоугольный треугольник определение угла

Чтобы определить функцию синуса острого угла α, начните с прямоугольный треугольник, содержащий угол измерения α; на сопроводительном рисунке угол α в треугольнике ABC представляет собой интересующий угол. Три стороны треугольника названы следующим образом:
- Противоположная сторона — это сторона, противоположная интересующему углу, в данном случае сторона a.
- Гипотенуза — это сторона, противоположная прямому углу, в эта сторона дела h. Гипотенуза всегда является самой длинной стороной прямоугольного треугольника.
- Соседняя сторона — это оставшаяся сторона, в данном случае сторона b. Он образует сторону (и примыкает) как к интересующему углу (углу A), так и к прямому углу.
После выбора такого треугольника синус угла равен длине противоположной стороны, деленное на длину гипотенузы:
- sin (α) = противоположная гипотенуза { displaystyle sin ( alpha) = { frac { textrm {Against}} { textrm {hypotenuse}}}}
Остальные тригонометрические функции угла можно определить аналогично; например, косинус угла — это отношение между соседней стороной и гипотенузой, а касательная дает отношение между противоположной и смежной сторонами.
Как указано, значение sin (α) { displaystyle sin ( alpha)}
Определение единичной окружности
В тригонометрии, единичная окружность — это окружность радиуса 1 с центром в начале координат (0, 0) в Декартова система координат.

Пусть прямая, проходящая через начало координат, пересекает единичную окружность, составляя угол θ с положительной половиной оси x. Координаты x и y этой точки пересечения равны cos (θ) и sin (θ) соответственно. Это определение согласуется с определением синуса и косинуса в прямоугольном треугольнике, когда 0 ° < θ < 90°: because the length of the hypotenuse of the unit circle is always 1, sin (θ) = противоположная гипотенуза = противоположная точка 1 = противоположная { displaystyle sin ( theta) = { tfrac { textrm {напротив}} { textrm {гипотенуза}}} = { tfrac { textrm {напротив}} {1}} = { textrm {напротив}}}


Использование определения единичной окружности имеет то преимущество, что угол может быть расширен до любого действительного аргумента. Этого также можно добиться, потребовав определенные симметрии, и чтобы синус был периодической функцией.
Анимация, показывающая, как функция синуса (красным) y = sin (θ) { displaystyle y = sin ( theta)}
строится по координате y (красная точка) точки на единичной окружности (зеленого цвета) под углом θ.
Идентификаторы
Точные идентификаторы (с использованием радиан ):
Они применяются для всех значений θ { displaystyle theta}
- sin (θ) знак равно соз (π 2 — θ) = 1 csc (θ) { displaystyle sin ( theta) = cos left ({ frac { pi} {2}} — theta right) = { frac {1} { csc ( theta)}}}
Взаимное
, обратное синуса — косеканс, т. е. обратное значение sin (A) это csc (A) или cosec (A). Косеканс дает отношение длины гипотенузы к длине противоположной стороны:
- csc (A) = 1 sin (A) = гипотенуза напротив = h a. { displaystyle csc (A) = { frac {1} { sin (A)}} = { frac { textrm {hypotenuse}} { textrm {напротив}}} = { frac {h} { a}}.}
Обратный

обратная функция синуса — это arcsine (arcsin или asin) или обратный синус (sin). Поскольку синус не является инъективным, это не точная обратная функция, а частичная обратная функция. Например, sin (0) = 0, но также sin (π) = 0, sin (2π) = 0 и т. Д. Отсюда следует, что функция арксинуса многозначна: arcsin (0) = 0, но также arcsin (0) = π, arcsin (0) = 2π и т. д. Когда требуется только одно значение, функция может быть ограничена ее главной ветвью. С этим ограничением для каждого x в домене выражение arcsin (x) будет оценивать только одно значение, называемое его главным значением.
- θ = arcsin (противоположная гипотенуза) = sin — 1 (ah). { displaystyle theta = arcsin left ({ frac { text {напротив}} { text {hypotenuse}}} right) = sin ^ {- 1} left ({ frac {a} { h}} right).}
где (для некоторого целого числа k):
- sin (y) = x ⟺ y = arcsin (x) + 2 π k, или y = π — arcsin ( Икс) + 2 π К { Displaystyle { begin {align} sin (y) = x iff y = arcsin (x) +2 pi k, { text {или}} \ y = pi — arcsin (x) +2 pi k end {align}}}
Или в одном уравнении:
- sin (y) = x ⟺ y = (- 1) k arcsin (x) + π К { displaystyle sin (y) = x iff y = (- 1) ^ {k} arcsin (x) + pi k}
По определению, арксинус удовлетворяет уравнению:
- sin (arcsin (x)) знак равно x { displaystyle sin ( arcsin (x)) = x !}
и
- arcsin (sin (θ)) = θ для — π 2 ≤ θ ≤ π 2. { displaystyle arcsin ( sin ( theta)) = theta quad { text {for}} — { frac { pi} {2}} leq theta leq { frac { pi} {2}}.}
Исчисление
Для функции синуса:
- f (x) = sin (x) { displaystyle f (x) = sin (x)}
Производная:
- f ‘(x) = cos (x) { displaystyle f’ (x) = cos (x)}
Первообразная:
- ∫ f (x) dx = — cos (x) + C { displaystyle int f (x) , dx = — cos (x) + C}
где C обозначает постоянную интегрирования.
Другие тригонометрические функции

sin (π / 2 — x) { displaystyle sin ( pi / 2-x)}

cos (x) { displaystyle cos (x)}

Любую тригонометрическую функцию можно выразить через любую другую (до знака плюс или минус или с помощью функции знака ).
В следующей таблице показано, как синус может быть выражен в терминах других общих тригонометрических функций :
| f θ | Использование плюса / минуса (±) | Использование функции знака (sgn) | |||||
|---|---|---|---|---|---|---|---|
| f θ = | ± на квадрант | f θ = | |||||
| I | II | III | IV | ||||
| соз | грех (θ) { displaystyle sin ( theta)} |
= ± 1 — cos 2 (θ) { displaystyle = pm { sqrt {1- cos ^ {2 } ( theta)}}} |
+ | + | − | − | = sign (соз (θ — π 2)) 1 — соз 2 (θ) { displaystyle = operatorname {sgn} left ( cos left ( theta — { frac { pi} {2}} right) right) { sqrt {1- cos ^ {2} ( theta)}}} |
cos (θ) { displaystyle соз ( theta)} |
= ± 1 — грех 2 (θ) { displaystyle = pm { sqrt {1- sin ^ {2} ( theta)}}} |
+ | − | − | + | = sgn (грех (θ + π 2)) 1 — грех 2 (θ) { displaystyle = operatorname {sgn} left ( sin left ( theta + { frac { pi} {2}} вправо) вправо) { sqrt {1- sin ^ {2} ( theta)}}} |
|
| кроватка | грех (θ) { displaystyle sin ( theta)} |
= ± 1 1 + детская кроватка 2 (θ) { displaysty le = pm { frac {1} { sqrt {1+ cot ^ {2} ( theta)}}}} |
+ | + | − | − | = sgn (детская кроватка (θ 2)) 1 1 + детская кроватка 2 (θ) { displaystyle = operatorname {sgn} left ( cot left ({ frac { theta} {2}} right) right) { frac {1} { sqrt {1+ кроватка ^ {2} ( theta)}}}} |
детская кроватка (θ) { displaystyle cot ( theta)} |
= ± 1 — sin 2 (θ) sin (θ) { displaystyle = pm { frac { sqrt {1- sin ^ {2} ( theta)}} { sin ( theta)}}} |
+ | − | − | + | = sgn (sin (θ + π 2)) 1 — грех 2 (θ) грех (θ) { displaystyle = operatorname {sgn} left ( sin left ( theta + { frac { pi} {2}} right) справа) { frac { sqrt {1- sin ^ {2} ( theta)}} { sin ( theta)}}} |
|
| tan | грех (θ) { displaystyle sin ( theta)} |
= ± загар (θ) 1 + загар 2 (θ) { displaystyle = pm { frac { tan ( theta)} { sqrt {1+ tan ^ { 2} ( theta)}}}} |
+ | − | − | + | = sign (tan (2 θ + π 4)) tan (θ) 1 + tan 2 (θ) { displaystyle = operatorname {sgn} left ( tan left ({ frac {2 theta + pi} {4}} right) right) { frac { tan ( theta)} { sqrt {1+ tan ^ {2 } ( theta)}}}} |
загар (θ) { Displaystyle загар ( theta)} |
= ± грех (θ) 1 — грех 2 (θ) { displaystyle = pm { frac { sin ( theta)} { sqrt {1- sin ^ {2} ( theta)}}}} |
+ | − | − | + | = sgn (sin (θ + π 2)) sin (θ) 1 — sin 2 (θ) { displaystyle = operatorname {sgn} left ( sin left ( theta + { frac { pi} {2}} right) right) { frac { sin ( theta)} { sqrt { 1- sin ^ {2} ( theta)}}}} |
|
| сек | грех (θ) { displaystyle sin ( theta)} |
= ± sec 2 (θ) — 1 сек (θ) { displaystyle = pm { frac { sqrt { sec ^ {2} ( theta) -1}} { sec ( theta)}}} |
+ | − | + | − | = sgn ( сек (4 θ — π 2)) сек 2 (θ) — 1 сек (θ) { displaystyle = operatorname {sgn} left ( sec left ({ frac {4 theta — pi } {2}} right) right) { frac { sqrt { sec ^ {2} ( theta) -1}} { sec ( theta)}}} |
сек (θ) { displaystyle sec ( theta)} |
= ± 1 1 — грех 2 (θ) { displaystyle = pm { frac {1} { sqrt {1- sin ^ {2} ( тета)}}}} |
+ | − | − | + | = знак (грех (θ + π 2)) 1 1 — грех 2 (θ) { displaystyle = operatorname {sgn} left ( sin left ( th eta + { frac { pi} {2}} right) right) { frac {1} { sqrt {1- sin ^ {2} ( theta)}}}} |
Для всех уравнения, которые используют плюс / минус (±), результат будет положительным для углов в первом квадранте.
Основное соотношение между синусом и косинусом также может быть выражено как тригонометрическое тождество Пифагора :
- cos 2 (θ) + sin 2 (θ) = 1 { displaystyle cos ^ {2} ( theta) + sin ^ {2} ( theta) = 1 !}
где sin (x) означает (sin (x)).
Функция синус-квадрата

На графике показаны как функция синуса, так и функция в квадрате синуса, причем синус отображается синим цветом, а синус в квадрате — красным. Оба графика имеют одинаковую форму, но с разными диапазонами значений и разными периодами. Синус в квадрате имеет только положительные значения, но в два раза больше периодов.
Функция квадрата синуса может быть выражена как модифицированная синусоида из тождества Пифагора и уменьшения мощности — с помощью формулы двойного угла косинуса:
- sin 2 (θ) = 1 — sin (2 θ + π 2) 2 { displaystyle sin ^ {2} ( theta) = { frac {1- sin (2 theta + { tfrac { pi} {2}})} {2} } }
Свойства, относящиеся к квадрантам

В таблице ниже показаны многие ключевые свойства синусоидальной функции (знак, монотонность, выпуклость), упорядоченные по квадрантам аргумента. Для аргументов, не указанных в таблице, можно вычислить соответствующую информацию, используя периодичность sin (α + 360 ∘) = sin (α) { displaystyle sin ( alpha +360 ^ { circ}) = sin ( alpha)}
| Квадрант | Градусы | Радианы | Значение | Знак | Монотонность | Выпуклость |
|---|---|---|---|---|---|---|
| 1-й квадрант | 0 ∘ < x < 90 ∘ {displaystyle 0^{circ } |
0 < x < π 2 {displaystyle 0 |
0 < sin ( x) < 1 {displaystyle 0<sin(x)<1} |
+ { displaystyle +} |
увеличение | вогнутый |
| 2-й квадрант | 90 ∘ < x < 180 ∘ {displaystyle 90^{circ } |
π 2 < x < π {displaystyle {frac {pi }{2}} |
0 < sin ( x) < 1 {displaystyle 0<sin(x)<1} |
+ { displaystyle +} |
уменьшение | вогнутый |
| 3-й квадрант | 180 ∘ < x < 270 ∘ {displaystyle 180^{circ } |
π < x < 3 π 2 {displaystyle pi  |
— 1 < sin ( x) < 0 {displaystyle -1<sin(x)<0} |
— { displaystyle -} |
уменьшение | выпуклый |
| 4-й квадрант | 270 ∘ < x < 360 ∘ {displaystyle 270^{circ } |
3 π 2 < x < 2 π {displaystyle {frac {3pi }{2}} |
— 1 < sin ( x) < 0 {displaystyle -1<sin(x)<0} |
— { displaystyle -} |
увеличение | выпуклое |

В следующей таблице приведены основная информация на границе квадрантов.
| Градусы | Радианы | грех (x) { displaystyle sin (x)} |
Тип точки |
|---|---|---|---|
0 ∘ { displaystyle 0 ^ { circ}} |
0 { displaystyle 0} |
0 { displaystyle 0} |
Корень, Inflection |
90 ∘ { displaystyle 90 ^ { circ}} |
π 2 { displaystyle { frac { pi} {2}}} |
1 { displaystyle 1} |
Максимум |
180 ∘ { displaystyle 180 ^ { circ}} |
π { displaystyle pi} |
0 { displaystyle 0} |
Корень, перегиб |
270 ∘ { displaystyle 270 ^ { circ}} |
3 π 2 { displaystyle { frac {3 pi } {2}}} |
— 1 { displaystyle -1} |
Минимум |
Определение ряда


Использование только геометрии и свойств ограничивает, можно показать, что производная синуса является косинусом, и что де Производная косинуса является отрицательной величиной синуса.
Использование отражения из вычисленного геометрического вывода синуса с (4n + k) -й производной в точке 0:
- sin (4 n + k) (0) = {0 когда k = 0 1, когда k = 1 0, когда k = 2 — 1, когда k = 3 { displaystyle sin ^ {(4n + k)} (0) = { begin {cases} 0 { text {when} } k = 0 \ 1 { text {when}} k = 1 \ 0 { text {when}} k = 2 \ — 1 { text {when}} k = 3 end {cases}} }
Это дает следующее разложение в ряд Тейлора при x = 0. Затем можно использовать теорию ряда Тейлора, чтобы показать, что следующие тождества выполняются для всех действительных чисел x ( где x — угол в радианах):
- sin (x) = x — x 3 3! + х 5 5! — х 7 7! + ⋯ знак равно ∑ N знак равно 0 ∞ (- 1) N (2 N + 1)! Икс 2 N + 1 { Displaystyle { begin {align} sin (x) = x — { frac {x ^ {3}} {3!}} + { frac {x ^ {5}} { 5!}} — { frac {x ^ {7}} {7!}} + Cdots \ [8pt] = sum _ {n = 0} ^ { infty} { frac {(-1) ^ {n}} {(2n + 1)!}} x ^ {2n + 1} \ [8pt] end {align}}}
Если бы x был выражен в градусах, тогда ряд содержал бы факторы, включающие степени π / 180: если x — количество градусов, количество радианов равно y = πx / 180, поэтому
- sin (xdeg) = sin (yrad) = π 180 x — (π 180) 3 х 3 3! + (π 180) 5 х 5 5! — (π 180) 7 х 7 7! + ⋯. { displaystyle { begin {align} sin (x _ { mathrm {deg}}) = sin (y _ { mathrm {rad}}) \ = { frac { pi} {180}} x- left ({ frac { pi} {180}} right) ^ {3} { frac {x ^ {3}} {3!}} + left ({ frac { pi} { 180}} right) ^ {5} { frac {x ^ {5}} {5!}} — left ({ frac { pi} {180}} right) ^ {7} { frac {x ^ {7}} {7!}} + cdots. end {align}}}
Формулы ряда для синуса и косинуса определяются однозначно, с точностью до выбора единицы для углов, согласно требованиям, что
- sin (0) = 0 и sin (2 x) = 2 sin (x) cos (x) cos 2 (x) + sin 2 (x) = 1 и соз (2 Икс) знак равно соз 2 (Икс) — грех 2 (Икс) { Displaystyle { begin {align} sin (0) = 0 { text {и}} sin (2x) = 2 sin (x) cos (x) \ cos ^ {2} (x) + sin ^ {2} (x) = 1 { text {and}} cos (2x) = cos ^ {2} (x) — sin ^ {2} (x) \ end {align}}}
Радиан — это единица, которая приводит к разложению с ведущим коэффициентом 1 для синуса и определяется дополнительное требование:
- sin (x) ≈ x, когда x ≈ 0. { displaystyle sin (x) приблизительно x { text {when}} x a pprox 0.}
Коэффициенты для серий синуса и косинуса, следовательно, могут быть получены путем подстановки их разложений в тождества пифагора и двойного угла, принимая ведущий коэффициент для синуса равным 1 и согласовывая остальные коэффициенты.
В общем, математически важные отношения между функциями синуса и косинуса и экспоненциальной функцией (см., Например, формулу Эйлера ) существенно упрощаются, когда углы выражаются в радианах, а не в градусах, градусах или других единицах. Поэтому в большинстве разделов математики, выходящих за рамки практической геометрии, считается, что углы выражаются в радианах.
Аналогичный ряд — это ряд Грегори для arctan, который получается путем опускания факториалов в знаменателе.
Непрерывная дробь
Функция синуса также может быть представлена как обобщенная непрерывная дробь :
- sin (x) = x 1 + x 2 2 ⋅ 3 — x 2 + 2 ⋅ 3 x 2 4 ⋅ 5 — x 2 + 4 ⋅ 5 x 2 6 ⋅ 7 — x 2 + ⋱. { displaystyle sin (x) = { cfrac {x} {1 + { cfrac {x ^ {2}} {2 cdot 3-x ^ {2} + { cfrac {2 cdot 3x ^ { 2}} {4 cdot 5-x ^ {2} + { cfrac {4 cdot 5x ^ {2}} {6 cdot 7-x ^ {2} + ddots}}}}}}}}.}
Представление непрерывной дроби может быть получено из формулы непрерывной дроби Эйлера и выражает вещественное число, как рациональное, так и иррациональное синусоидальной функции.
Фиксированная точка
Ноль — единственная действительная фиксированная точка синусоидальной функции; другими словами, единственное пересечение синусоидальной функции и тождественной функции — это sin (0) = 0.
Длина дуги
Длина дуги синусоидальной кривой между a { displaystyle a}


Длина дуги для полного периода равна 4 2 π 3 Γ (1/4) 2 + Γ (1/4) 2 2 π = 7.640395578 … { Textstyle { frac {4 { sqrt {2 pi ^ {3}}}} { Gamma (1/4) ^ {2}}} + { frac { Gamma (1/4) ^ {2}} { sqrt {2 pi}}} = 7.640395578 ldots}

Длина дуги синусоидальной кривой от 0 до x равна приведенному выше числу, деленному на 2 π { displaystyle 2 pi}

- 1,21600672 x + 0,10317093 sin (2 x) — 0,00220445 sin (4 x) + 0,00012584 sin (6 x) — 0,00001011 sin (8 x) + ⋯ { displaystyle 1.21600672x + 0.10317093 sin (2x) -0.00220445 sin (4x) +0.00012584 sin (6x) -0.00001011 sin (8x) + cdots}
Главный член в приведенном выше уравнении и предел отношение длины дуги к расстоянию определяется следующим образом:
- π 2 + 2 Γ (3 4) 4 2 π 3/2 Γ (3 4) 2 { displaystyle { frac { pi ^ {2} +2 Гамма left ({ frac {3} {4}} right) ^ {4}} {{ sqrt {2}} pi ^ {3/2} Gamma left ({ frac {3} { 4}} right) ^ {2}}}}
Закон синусов
Закон синусов гласит, что для произвольного треугольника со сторонами a, b и c и углы, противоположные этим сторонам A, B и C:
- sin A a = sin B b = sin C c. { displaystyle { frac { sin A} {a}} = { frac { sin B} {b}} = { frac { sin C} {c}}.}
Это эквивалентно равенство первых трех выражений ниже:
- a sin sin A = b sin B = c sin C = 2 R, { displaystyle { frac {a} { sin A}} = { frac { b} { sin B}} = { frac {c} { sin C}} = 2R,}
где R — описанный радиус треугольника.
Это можно доказать, разделив треугольник на два правильные и используя приведенное выше определение синуса. Закон синусов полезен для вычисления длин неизвестных сторон треугольника, если известны два угла и одна сторона. Это обычная ситуация, возникающая в триангуляции, методе определения неизвестных расстояний путем измерения двух углов и доступного замкнутого расстояния.
Особые значения

Для некоторых целых чисел x градусов, значение sin (x) особенно просто. Таблица некоторых из этих значений приведена ниже.
| x (угол) | sin (x) | ||||
|---|---|---|---|---|---|
| Градусы | Радианы | Градианы | Повороты | Точное значение | Десятичное число |
| 0° | 0 | 0 | 0 | 0 | 0 |
| 180 ° | π | 200 | 1/2 | ||
| 15 ° | 1 / 12π | 16+2/3 | 1/24 | 6 — 2 4 { displaystyle { frac {{ sqrt {6}} — { sqrt {2}}} {4}}} |
0,258819045102521 |
| 165 ° | 11 / 12π | 183 + 1/3 | 11/24 | ||
| 30 ° | 1 / 6π | 33+1/3 | 1/12 | 1/2 | 0,5 |
| 150 ° | 5 / 6π | 166+2/3 | 5/12 | ||
| 45 ° | 1 / 4π | 50 | 1/8 | 2 2 { displaystyle { frac { sqrt {2}} {2}}} |
0,707106781186548 |
| 135 ° | 3 / 4π | 150 | 3/8 | ||
| 60 ° | 1 / 3π | 66 + 2/3 | 1/6 | 3 2 { displaystyle { frac { sqrt {3}} {2}}} |
0,866025403784439 |
| 120 ° | 2 / 3π | 133+1/3 | 1/3 | ||
| 75 ° | 5 / 12π | 83 + 1/3 | 5/24 | 6 + 2 4 { displaystyle { frac {{ sqrt {6}} + { sqrt {2}}} {4}}} |
0,965925826289068 |
| 105 ° | 7 / 12π | 116 + 2/3 | 7/24 | ||
| 90 ° | 1 / 2π | 100 | 1/4 | 1 | 1 |
с шагом 90 градусов:
| x в градусах | 0° | 90 ° | 180 ° | 270 ° | 360 ° |
| x в радианах | 0 | π / 2 | π | 3π / 2 | 2π |
| x в углах | 0 | 100 | 200 | 300 | 400 |
| x по очереди | 0 | 1/4 | 1/2 | 3/4 | 1 |
| sin x | 0 | 1 | 0 | -1 | 0 |
Другие значения, не указанные выше:
- sin (π 60) знак равно грех (3 ∘) знак равно (2–12) 5 + 5 + (10–2) (3 + 1) 16 { displaystyle sin left ({ frac { pi} {60}} right) = sin (3 ^ { circ}) = { frac {(2 — { sqrt {12}}) { sqrt {5 + { sqrt {5}}}} + ({ sqrt {10} } — { sqrt {2}}) ({ sqrt {3}} + 1)} {16}}}
OEIS : A019812
- грех (π 30) = грех (6 ∘) = 30 — 180 — 5 — 1 8 { displaystyle sin left ({ frac { pi} {30}} right) = sin (6 ^ { circ}) = { frac {{ sqrt {30 — { sqrt {180}}}} — { sqrt {5}} — 1} {8}}}
OEIS : A019815
- грех (π 20) знак равно грех (9 ∘) = 10 + 2-20-80 8 { displaystyle sin left ({ frac { pi} {20}} right) = sin (9 ^ { circ}) = { frac {{ sqrt {10}} + { sqrt {2}} — { sqrt {20 — { sqrt {80}}}}} {8}}}
OEIS : A019818
- грех (π 15) = грех (12 ∘) = 10 + 20 + 3-15 8 { displaystyle sin left ({ frac { pi} {15}} right) = sin (12 ^ { circ}) = { frac {{ sqrt {10 + { sqrt {20}}}} + { sqrt {3}} — { sqrt {15}}} {8}}}
OEIS : A019821
- грех (π 10) = грех (18 ∘) = 5 — 1 4 = 1 2 φ — 1 { displaystyle sin left ({ frac { pi} {10}} right) = sin (18 ^ { circ}) = { frac {{ sqrt {5}} — 1} {4}} = { tfrac {1} {2}} varphi ^ {- 1}}
OEIS : A019827
- sin (7 π 60) = sin (21 ∘) = (2 + 12) 5-5 — (10 + 2) (3-1) 16 { displaystyle sin left ({ frac {7 pi} {60}} right) = sin (21 ^ { circ}) = { frac {(2+ { sqrt {12}}) { sqrt {5 — { sqrt {5}}}} — ({ sqrt {10}} + { sqrt {2}}) ({ sqrt {3}} — 1)} {16}}}
OEIS : A019830
- грех (π
= грех (22,5 ∘) = 2–2 2 { displaystyle sin left ({ frac { pi} {8}} right) = sin (22,5 ^ { circ}) = { frac { sqrt {2 — { sqrt {2}}}} {2}}}
- грех (2 π 15) = грех (24 ∘) = 3 + 15 — 10 — 20 8 { displaystyle sin left ({ frac {2 pi} {15}} right) = sin (24 ^ { circ}) = { frac {{ sqrt { 3}} + { sqrt {15}} — { sqrt {10 — { sqrt {20}}}}} {8}}}
OEIS : A019833
- грех (3 π 20) знак равно грех (27 ∘) = 20 + 80-10 + 2 8 { displaystyle sin left ({ frac {3 pi} {20}} right) = sin (27 ^ { circ}) = { frac {{ sqrt {20 + { sqrt {80}}}} — { sqrt {10}} + { sqrt {2}}} {8}}}
OEIS : A019836
- грех (11 π 60) = грех (33 ∘) = (12–2) 5 + 5 + (10–2) (3 + 1) 16 { displaystyle sin left ({ frac {11 pi} {60}} right) = sin (33 ^ { circ}) = { frac {({ sqrt {12}} — 2) { sqrt {5 + { sqrt {5}}}} + ({ sqrt {10}} — { sqrt {2}}) ({ sqrt {3}} + 1)} {16}}}
OEIS : A019842
- грех (π 5) = грех (36 ∘) = 10-20 4 { displaystyle sin left ({ frac { pi} {5}} справа) = sin (36 ^ { circ}) = { frac { sqrt {10 — { sqrt {20}}}} {4}}}
OEIS : A019845
- грех (13 π 60) = грех (39 ∘) = (2–12) 5–5 + (10 + 2) (3 + 1) 16 { displaystyle sin left ({ frac {13 число Пи } {60}} right) = sin (39 ^ { circ}) = { frac {(2 — { sqrt {12}}) { sqrt {5 — { sqrt {5}}}} + ({ sqrt {10}} + { sqrt {2}}) ({ sqrt {3}} + 1)} {16}}}
OEIS : A019848
- грех (7 π 30) знак равно грех (42 ∘) = 30 + 180 — 5 + 1 8 { displaystyle sin left ({ frac {7 pi} {30}} right) = sin ( 42 ^ { circ}) = { frac {{ sqrt {30 + { sqrt {180}}}} — { sqrt {5}} + 1} {8}}}
OEIS : A019851
Связь с комплексными числами

Синус используется для определения мнимой части комплексного числа , заданного в полярных координатах. (г, φ):
- Z знак равно р (соз (φ) + я грех (φ)) { Displaystyle Z = г ( соз ( varphi) + я грех ( varphi))}
мнимая часть:
- Im (z) = r sin (φ) { displaystyle operatorname {Im} (z) = r sin ( varphi)}
r и φ представляют собой величину и угол комплексного числа соответственно. i — это мнимая единица. z — комплексное число ..
Несмотря на то, что мы имеем дело с комплексными числами, параметр синуса в этом случае по-прежнему является действительным числом. Синус также может принимать в качестве аргумента комплексное число.
Синус с комплексным аргументом
sin (z) { displaystyle sin (z)}


sin (θ) { displaystyle sin ( theta)}

ei θ { displaystyle e ^ {i theta}}

Определение синусоидальной функции для комплексных аргументов z:
- sin (z) = ∑ n = 0 ∞ (- 1) n ( 2 п + 1)! z 2 N + 1 знак равно eiz — е — iz 2 i = sinh (iz) i { displaystyle { begin {align} sin (z) = sum _ {n = 0} ^ { infty} { frac {(-1) ^ {n}} {(2n + 1)!}} z ^ {2n + 1} \ = { frac {e ^ {iz} -e ^ {- iz}} { 2i}} \ = { frac { sinh left (iz right)} {i}} end {align}}}
где i = −1, а sinh — гиперболический синус. Это целая функция. Кроме того, для чисто вещественного x
- sin (x) = Im (e i x). { displaystyle sin (x) = operatorname {Im} (e ^ {ix}).}
Для чисто мнимых чисел:
- sin (i y) = i sinh (y). { displaystyle sin (iy) = i sinh (y).}
Также иногда полезно выразить сложную синусоидальную функцию в терминах действительной и мнимой частей ее аргумента:
- sin (x + iy) = sin (x) cos (iy) + cos (x) sin (iy) = sin (x) cosh (y) + i cos (x) sinh (y). { Displaystyle { begin {align} sin (x + iy) = sin (x) cos (iy) + cos (x) sin (iy) \ = sin (x) cosh (y) + i cos (x) sinh (y). end {align}}}
Разложение на частичную дробь и произведение комплексного синуса
Использование техники разложения на частичную дробь в комплексный анализ, можно найти, что бесконечный ряд
- ∑ n = — ∞ ∞ (- 1) nz — n = 1 z — 2 z ∑ n = 1 ∞ (- 1) nn 2 — z 2 { displaystyle { begin {align} sum _ {n = — infty} ^ { infty} { frac {(-1) ^ {n}} {zn}} = { frac {1} {z} } -2z sum _ {n = 1} ^ { infty} { frac {(-1) ^ {n}} {n ^ {2} -z ^ {2}}} end {выровнено}}}
сходятся и равны π sin (π z) { textstyle { frac { pi} { sin ( pi z)}}}
- π 2 sin 2 (π z) = ∑ n = — ∞ ∞ 1 (z — n) 2. { displaystyle { begin {align} { frac { pi ^ {2}} { sin ^ {2} ( pi z)}} = sum _ {n = — infty} ^ { infty} { frac {1} {(zn) ^ {2}}}. end {align}}}
Используя технику расширения произведения, можно вывести
- sin (π z) = π z ∏ n = 1 ∞ (1 — z 2 n 2). { displaystyle { begin {align} sin ( pi z) = pi z prod _ {n = 1} ^ { infty} left (1 — { frac {z ^ {2}} {n ^{2}}}right).end{aligned}}}
Alternatively, the infinite product for the sine can be proved using complex Fourier series.
| Proof of the infinite product for the sine |
|---|
|
Using complex Fourier series, the function cos ( zx) {displaystyle cos(zx)}
Setting x = π {displaystyle x=pi }
Therefore we get
The function π cot ( π z) {displaystyle pi cot(pi z)}
Exponentiating gives
Since lim z → 0 sin ( π z) z = π {textstyle lim _{zto 0}{frac {sin(pi z)}{z}}=pi }
for some open and connected subset of C {displaystyle mathbb {C} } |
Usage of complex sine
sin(z) is found in the functional equation for the Gamma function,
- Γ ( s) Γ ( 1 − s) = π sin ( π s), {displaystyle Gamma (s)Gamma (1-s)={pi over sin(pi s)},}
which in turn is found in the functional equation for the Riemann zeta-function,
- ζ ( s) = 2 ( 2 π) s − 1 Γ ( 1 − s) sin ( π s / 2) ζ ( 1 − s). {displaystyle zeta (s)=2(2pi)^{s-1}Gamma (1-s)sin(pi s/2)zeta (1-s).}
As a holomorphic function, sin z is a 2D solution of Laplace’s equation :
- Δ u ( x 1, x 2) = 0. {displaystyle Delta u(x_{1},x_{2})=0.}
The complex sine function is also related to the level curves of pendulums.
Complex graphs
 |
 |
 |
| real component | imaginary component | magnitude |
.
 |
 |
 |
| real component | imaginary component | magnitude |
History
While the early study of trigonometry can be traced to antiquity, the trigonometric functions as they are in use today were developed in the medieval period. The chord function was discovered by Hipparchus of Nicaea (180–125 BCE) and Ptolemy of Rom Египет (90–165 гг. н. э.).
Функцию синуса и версин (1 — косинус) можно проследить до функций jyā и koṭi-jyā, используемых в период Гупты (320–550 гг. Н. Э.) Индийская астрономия (Арьябхатия, Сурья Сиддханта ) посредством перевода с санскрита на арабский, а затем с арабского на латинский.
Все шесть используемых в настоящее время тригонометрических функций были известны в исламской математике к 9 веку, как и закон синусов, использовавшийся в решении треугольников. За исключением синуса (который был заимствован из индийской математики), арабскими математиками были открыты другие пять современных тригонометрических функций, включая косинус, тангенс, котангенс, секанс и косеканс. Аль-Хваризми (ок. 780–850) составил таблицы синусов, косинусов и тангенсов. Мухаммад ибн Джабир аль-Харрани аль-Баттани (853–929) открыл взаимные функции секанса и косеканса и создал первую таблицу косекансов. для каждой степени от 1 ° до 90 °.
Первое опубликованное использование сокращений sin, cos и tan принадлежит французскому математику 16 века Альбер Жирар ; в дальнейшем они были обнародованы Эйлером (см. ниже). Opus palatinum de triangulis Георга Иоахима Ретикуса, ученика Коперника, вероятно, был первым в Европе, который определил тригонометрические функции непосредственно в терминах прямоугольных треугольников, а не окружностей, с таблицами для все шесть тригонометрических функций; эта работа была закончена учеником Ретикуса Валентином Отоном в 1596 году.
В статье, опубликованной в 1682 году, Лейбниц доказал, что sin x не является алгебраической функцией x Роджер Котес вычислил производную синуса в своей Harmonia Mensurarum (1722). Введение Леонарда Эйлера в анализ бесконечности (1748) в основном отвечало за установление аналитического подхода к тригонометрическим функциям. в Европе, также определяя их как бесконечные серии и представляя «формулу Эйлера », а также почти современные сокращения sin., cos., tang., cot., sec. и cosec.
Этимология
| Найдите sine в Wiktionary, бесплатном словаре. |
Этимологически слово синус происходит от санскрита слово, обозначающее аккорд, jiva * (jya — его более популярный синоним). Это было транслитерировано на арабском как jiba جيب, что, однако, не имеет смысла на этом языке и сокращается как jb جب. Поскольку арабский язык написан без коротких гласных, «jb» интерпретировалось как слово jaib جيب, что означает «грудь». Когда в XII веке арабские тексты были переведены на латинский Герардом Кремонским, он использовал латинский эквивалент слова «лоно», sinus (что означает « лоно »или« гнедой »или« складкой »). Джерард, вероятно, был не первым ученым, использовавшим этот перевод; Роберт Честерский, кажется, предшествовал ему, и есть свидетельства более раннего использования. Английская форма синуса была введена в 1590-х годах.
Программные реализации
Не существует стандартного алгоритма для вычисления синуса. IEEE 754-2008, наиболее широко используемый стандарт для вычислений с плавающей запятой, не касается вычисления тригонометрических функций, таких как синус. Алгоритмы вычисления синуса могут быть сбалансированы с учетом таких ограничений, как скорость, точность, переносимость или диапазон принимаемых входных значений. Это может привести к разным результатам для разных алгоритмов, особенно для особых обстоятельств, таких как очень большие входные данные, например sin (10).
Некогда распространенная оптимизация программирования, особенно используемая в трехмерной графике, заключалась в предварительном вычислении таблицы значений синуса, например, одно значение на градус. Это позволяло искать результаты в таблице, а не рассчитывать их в реальном времени. С современной архитектурой ЦП этот метод не может дать никаких преимуществ.
Алгоритм CORDIC обычно используется в научных калькуляторах.
Функция синуса, наряду с другими тригонометрическими функциями, широко доступна для разных языков и платформ программирования. В вычислениях это обычно сокращается до sin.
Некоторые архитектуры ЦП имеют встроенную инструкцию для синуса, включая FPU Intel x87 начиная с 80387.
В языках программирования sinобычно либо встроенная функция, либо находится в стандартной математической библиотеке языка.
Например, стандартная библиотека C определяет синусоидальные функции в пределах math.h : sin (double ), sinf (float )и sinl (long double ). Параметром каждого из них является значение с плавающей запятой, определяющее угол в радианах. Каждая функция возвращает тот же тип данных , который принимает.Множество других тригонометрических функций также определены в math.h, например, для косинуса, арксинуса и гиперболического синуса (sinh).
Аналогично, Python определяет math.sin (x)во встроенном модуле math. Сложные синусоидальные функции также доступны в Модуль cmath, например, cmath.sin (z). Математические функции CPython вызывают библиотеку C mathи используют Формат с плавающей запятой двойной точности.
.
Реализации на основе поворотов
Некоторые программные библиотеки предоставляют реализации синусоиды с использованием входного угла в половину- оборотов, где пол-оборота составляет угол 180 градусы или π { displaystyle pi}
| Окружение | Название функции | Угловые единицы |
|---|---|---|
| MATLAB | sinpi |
полуобороты |
| OpenCL | sinpi |
полуобороты |
| R | sinpi |
полуобороты |
| Julia | sinpi |
полуобороты |
| CUDA | sinpi |
полуобороты |
| ARM | sinpi |
полуобороты |
Преимущество точности проистекает из способности идеально представлять ключевые углы, такие как полный оборот, полуоборот и четверть оборота, без потерь в двоичной системе с плавающей запятой или с фиксированной запятой. Напротив, представляя 2 π { displaystyle 2 pi}


Повороты также имеют преимущество в точности и эффективности для вычисления по модулю до одного периода. Вычисление по модулю 1 оборот или по модулю 2 полуоборотов может выполняться без потерь и эффективно как с плавающей, так и с фиксированной точкой. Например, вычисление по модулю 1 или 2 для значения с фиксированной запятой, масштабированного по двоичной точке, требует только битового сдвига или операции побитового И. Напротив, вычисление по модулю π 2 { displaystyle { frac { pi} {2}}}

Для приложений, связанных с датчиками угла, датчик обычно обеспечивает угловые измерения в форме, напрямую совместимой с поворотами или полуоборотами. Например, датчик угла может отсчитывать от 0 до 4096 за один полный оборот. Если полуворота используются в качестве единицы измерения угла, тогда значение, предоставляемое датчиком, напрямую и без потерь отображается в тип данных с фиксированной точкой с 11 битами справа от двоичной точки. Напротив, если радианы используются в качестве единицы для хранения угла, то неточности и стоимость умножения необработанного целого числа датчика на приближение к π 2048 { displaystyle { frac { pi} {2048}}}
См. Также
- таблицу синусов Рьябханы
- Формула аппроксимации синуса Бхаскары I
- Дискретное синусоидальное преобразование
- Формула Эйлера
- Обобщенная тригонометрия
- Гиперболическая функция
- Закон синусов
- Список периодических функций
- Список тригонометрических тождеств
- Серия Мадхав
- Таблица синусов Мадхавы
- Теорема оптического синуса
- Полярный синус — обобщение на углы вершин
- Доказательства тригонометрических тождества
- функция Sinc
- преобразования синуса и косинуса
- интеграл синуса
- квадрант синуса
- волна синуса
- уравнение синуса – Гордона
- синусоидальная модель
- тригонометрические функции
- тригонометрический интеграл
Цитаты
Ссылки
- Траупман, доктор философии, Джон К. (1966), Латинский и английский словарь Нью-колледжа, Торонто: Bantam, ISBN 0-553-27619-0
- Седьмой новый университетский словарь Вебстера, Спрингфилд: G. C. Merriam Company, 1969
Внешние ссылки
СМИ, связанные с функцией синуса на Wikimedia Commons
| Найдите sine в Wiktionary, бесплатном словаре. |
Уравнения разложения тригонометрических функций:квадрат синус альфа, косинус альфа, тангенс альфа, котангенс альфа.
Формулы преобразования функций двойного угла (2α) в выражение через одинарный угол (α)
sin(2α)- через sin и cos:
sin(2α)- через tg и ctg:
cos(2α)- через sin и cos:
cos(2α)- через tg и ctg:
tg(2α) и сtg(2α):
Формулы преобразования функций (синус, косинус, тангенс, котангенс), тройного угла (3α) в выражение через одинарный угол (α):
Тригонометрические формулы преобразования разности аргументов
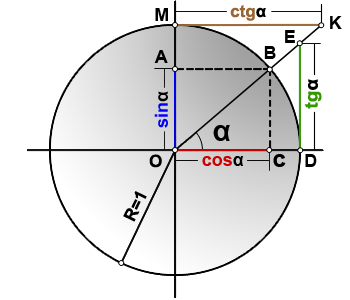
sin(α)=OA
cos(α)=OC
tg(α)=DE
ctg(α)=MK
R=OB=1
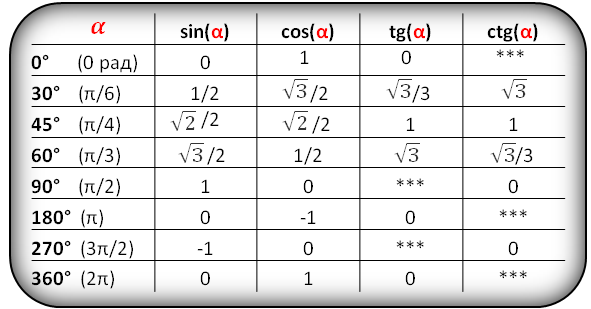
Значения функций для некоторых углов, α
В таблице показаны формулы приведения для тригонометрических функций (sin, cos, tg, ctg).
СИНУС
- СИНУС
-
— одна из тригонометрич. функций: у = sinx. Область определения — вся числовая прямая, область значений — отрезок [-1; 1]; С.- функция нечетная, периодическая с периодом 2p. С. и косинус связаны формулой sin2 x +cos2 х =1, С. и косеканс связаны формулой
Производная С.:
(sin x)’ = cos x. Интеграл от С.:
С. разлагается в степенной ряд:
Функция, обратная С., наз. арксинусом. С. и косинус комплексного аргумента z связаны с показательной функцией формулами Эйлера
если z=ix (чисто мнимое число), то
где shx — гиперболич. синус.
Ю. А. Горьков.
Математическая энциклопедия. — М.: Советская энциклопедия.
.
1977—1985.
Синонимы:
Смотреть что такое «СИНУС» в других словарях:
-
СИНУС — (лат.). Тригонометрическая величина означающая половину хорды двойной дуги или угла а также перпендикуляр, опущенный из конца дуги на радиус. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. СИНУС в тригонометрии… … Словарь иностранных слов русского языка
-
СИНУС — • СИНУС, в анатомии пазуха, углубление, впадина, выпячивание, расширение, длинный замкнутый канал (например, венозный синус, каротидный синус). • СИНУС, в ТРИГОНОМЕТРИИ отношение длины противолежащего (для данного острого угла) катета к длине… … Научно-технический энциклопедический словарь
-
СИНУС — в анатомии пазуха, углубление, впадина, выпячивание, расширение, длинный замкнутый канал (напр., венозный синус, каротидный синус) … Большой Энциклопедический словарь
-
СИНУС — 1. СИНУС1, синуса, муж. (лат. sinus изгиб, кривизна) (мат.). Тригонометрическая функция угла, в прямоугольном треугольнике равная отношения катета, противолежащего углу, к гипотенузе. 2. СИНУС2, синуса, муж. (лат. sinus изгиб, кривизна) (анат.).… … Толковый словарь Ушакова
-
СИНУС — 1. СИНУС1, синуса, муж. (лат. sinus изгиб, кривизна) (мат.). Тригонометрическая функция угла, в прямоугольном треугольнике равная отношения катета, противолежащего углу, к гипотенузе. 2. СИНУС2, синуса, муж. (лат. sinus изгиб, кривизна) (анат.).… … Толковый словарь Ушакова
-
СИНУС — мат. отвес с конца дуги на луч (радиус). Обращенный синус, косинус, часть луча, меж дуги и синуса. Толковый словарь Даля. В.И. Даль. 1863 1866 … Толковый словарь Даля
-
синус — канал, пазуха, функция, углубление Словарь русских синонимов. синус сущ., кол во синонимов: 4 • канал (68) • пазуха … Словарь синонимов
-
СИНУС — (sine) Соотношение в прямоугольном треугольнике между стороной, противоположной углу, и гипотенузой. Синус угла х пишется как sin x. Если описывается круг единичного радиуса, измерение углов начинается с востока против часовой стрелки; sin x –… … Экономический словарь
-
СИНУС — (лат. sinus) одна из тригонометрических функций … Большой Энциклопедический словарь
-
Синус — верзус см. Тригонометрия … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
-
Синус — верзус см. Тригонометрия … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона






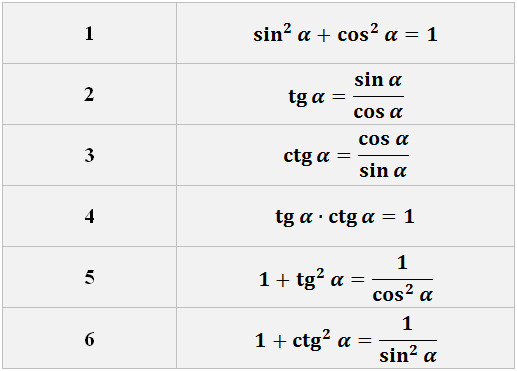
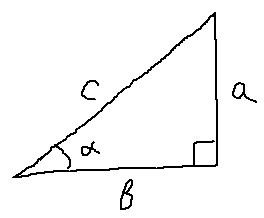
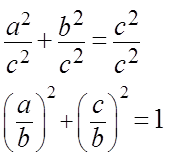
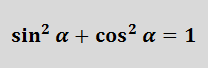
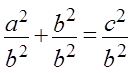
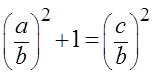
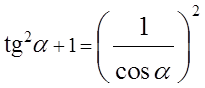
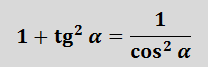
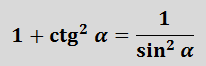
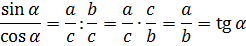
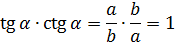
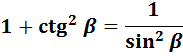
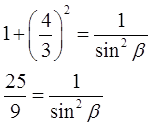
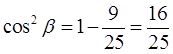
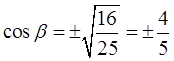
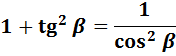
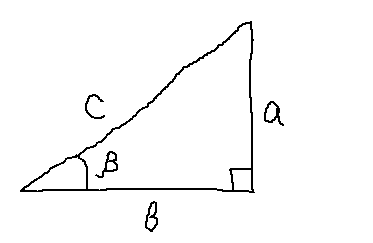
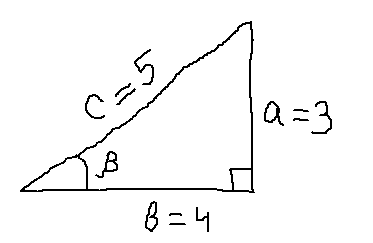
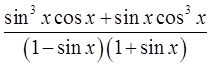
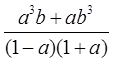
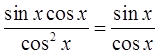
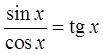
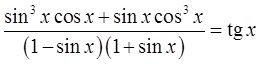
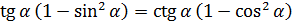
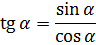
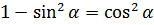
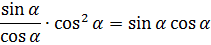
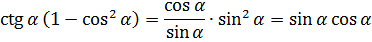
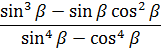
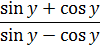
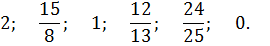


 строится по координате y (красная точка) точки на единичной окружности (зеленого цвета) под углом θ.
строится по координате y (красная точка) точки на единичной окружности (зеленого цвета) под углом θ.












![{ displaystyle { begin {align} sin (x) = x - { frac {x ^ {3}} {3!}} + { Frac {x ^ {5}} {5!}} - { frac {x ^ {7}} {7!}} + Cdots \ [8pt] = sum _ {n = 0} ^ { infty} { frac {(-1) ^ {n}} {(2n + 1)!}} x ^ {2n + 1} \ [8pt] end {выровнено}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/def345e147219a7892eb8140dfeb1c77b29dce38)








 OEIS : A019812
OEIS : A019812  OEIS : A019815
OEIS : A019815  OEIS : A019818
OEIS : A019818  OEIS : A019821
OEIS : A019821  OEIS : A019827
OEIS : A019827  OEIS : A019830
OEIS : A019830  = грех (22,5 ∘) = 2–2 2 { displaystyle sin left ({ frac { pi} {8}} right) = sin (22,5 ^ { circ}) = { frac { sqrt {2 — { sqrt {2}}}} {2}}}
= грех (22,5 ∘) = 2–2 2 { displaystyle sin left ({ frac { pi} {8}} right) = sin (22,5 ^ { circ}) = { frac { sqrt {2 — { sqrt {2}}}} {2}}}
 OEIS : A019833
OEIS : A019833  OEIS : A019836
OEIS : A019836  OEIS : A019842
OEIS : A019842  OEIS : A019845
OEIS : A019845  OEIS : A019848
OEIS : A019848  OEIS : A019851
OEIS : A019851 










 can be decomposed as
can be decomposed as![{ displaystyle cos (zx) = { frac {z sin ( pi z)} { pi}} displaystyle sum _ {n = - infty} ^ { infty} { frac {(-1) ^ {n} , e ^ {inx}} {z ^ { 2} -n ^ {2}}}, , z in mathbb {C} setminu s { mathbb {Z} }, , x in [- pi, pi].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/99f892c035938064b0ca52b732ef6265e86a052f)
 yields
yields

 is the derivative of ln ( sin ( π z)) + C 0 {displaystyle ln(sin(pi z))+C_{0}}
is the derivative of ln ( sin ( π z)) + C 0 {displaystyle ln(sin(pi z))+C_{0}} . Furthermore, if d f d z = z z 2 − n 2 {textstyle {frac {df}{dz}}={frac {z}{z^{2}-n^{2}}}}
. Furthermore, if d f d z = z z 2 − n 2 {textstyle {frac {df}{dz}}={frac {z}{z^{2}-n^{2}}}} , then the function f {displaystyle f}
, then the function f {displaystyle f} such that the emerged series converges is f = 1 2 ln ( 1 − z 2 / n 2) + C 1 {textstyle f={frac {1}{2}}ln(1-z^{2}/n^{2})+C_{1}}
such that the emerged series converges is f = 1 2 ln ( 1 − z 2 / n 2) + C 1 {textstyle f={frac {1}{2}}ln(1-z^{2}/n^{2})+C_{1}} , which can be proved using the Weierstrass M-test. The interchange of the sum and derivative is justified by uniform convergence. It follows that
, which can be proved using the Weierstrass M-test. The interchange of the sum and derivative is justified by uniform convergence. It follows that

 and lim z → 0 ∏ n = 1 ∞ ( 1 − z 2 n 2) = 1 {textstyle lim _{zto 0}prod _{n=1}^{infty }left(1-{frac {z^{2}}{n^{2}}}right)=1}
and lim z → 0 ∏ n = 1 ∞ ( 1 − z 2 n 2) = 1 {textstyle lim _{zto 0}prod _{n=1}^{infty }left(1-{frac {z^{2}}{n^{2}}}right)=1} , we have e C = π {displaystyle e^{C}=pi }
, we have e C = π {displaystyle e^{C}=pi } . Hence
. Hence
 . Let a n ( z) = − z 2 n 2 {displaystyle textstyle {a_{n}(z)=-{frac {z^{2}}{n^{2}}}}}
. Let a n ( z) = − z 2 n 2 {displaystyle textstyle {a_{n}(z)=-{frac {z^{2}}{n^{2}}}}} . Since ∑ n = 1 ∞ | a n ( z) | {displaystyle textstyle {sum _{n=1}^{infty }|a_{n}(z)|}}
. Since ∑ n = 1 ∞ | a n ( z) | {displaystyle textstyle {sum _{n=1}^{infty }|a_{n}(z)|}} converges uniformly on any closed disk, ∏ n = 1 ∞ ( 1 + a n ( z)) {displaystyle textstyle {prod _{n=1}^{infty }(1+a_{n}(z))}}
converges uniformly on any closed disk, ∏ n = 1 ∞ ( 1 + a n ( z)) {displaystyle textstyle {prod _{n=1}^{infty }(1+a_{n}(z))}} converges uniformly on any closed disk as well. It follows that the infinite product is holomorphic on C {displaystyle mathbb {C} }
converges uniformly on any closed disk as well. It follows that the infinite product is holomorphic on C {displaystyle mathbb {C} } , which completes the proof. ◼ {displaystyle blacksquare }
, which completes the proof. ◼ {displaystyle blacksquare }