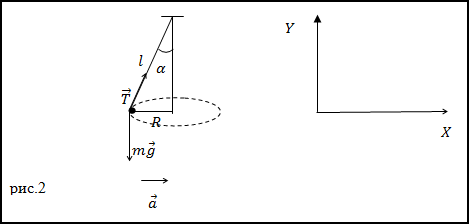Сила натяжения как пишется - Napishi.top - правописание и грамматика

Сила натяжения нити — формулировка

Определение

Силой натяжения называют силу, приложенную к концам объекта и создающую внутри него упругую деформацию.

Длина тела, к которому приложена сила, обычно многократно больше, чем его толщина. Примерами таких объектов являются веревка, канат, трос, леска, проволока. Сила натяжения визуально проявляется в следующих примерах:

создание строительного отвеса;
установка растяжек для фиксации радиоантенн;
поведение арматуры внутри напряженного бетона;
устройство корабельного такелажа.

Как определить силу, формулы

Натяжение проявляется по-разному. Поэтому сила натяжения может рассчитываться определенным образом, в зависимости от окружающих условий.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

С неподвижно закрепленным верхним концом

Простейшим примером проявления силы натяжения является нить с закрепленным на ней грузом. Верхний конец такого подвеса фиксируется неподвижно. В этом случае сила натяжения будет соответствовать силе тяжести, которая действует на тело. Формула для расчета:

(F=F_{тяж}=m*g)

где m – это масса тела, а g представляет собой ускорение свободного падения.

Если нить под углом

В случае, когда груз расположен под определенным углом, характер силы натяжения несколько изменяется. Примером такой системы выступает маятник.

(F_n=m*g*cos(a))

где а равен углу отклонения.

Формула с учетом ускорения и массы

В ситуации, при которой на груз оказывается сила натяжения, приводящая его в движение вверх, следует использовать такую формулу для ее расчета:

(F=F_{тяж}+m*a)

Сила натяжения во вращающейся системе

Описание

Такое явление можно наблюдать, когда система из нити и тела вращается во время раскручивания подвеса вокруг своей оси с закрепленным на одном его конце объектом: центрифуга, маятник, качели. Сила натяжения, возникающая внутри подвеса, характеризуется центробежной силой и в условиях вращения в вертикальной плоскости циклически претерпевает изменения. То есть можно наблюдать зависимость силы от угла отклонения от вертикали:

приближение к земле приводит к увеличению силы;
во время удаления от земли сила слабеет.

Формула расчета

Рассчитать силу натяжения в условиях вращающейся системы можно так:

(F=frac{mtimes nu ^{2}}{r})

Обозначение, единица измерения

Существуют определенные стандарты для написания формулы силы натяжения. Как и другие физические силы, натяжение обозначается F. В качестве единицы измерения используют Ньютон (H)

(H=frac{kgtimes m}{c^{2}})

Примеры решения задач

Задание 1

На невесомую нерастяжимую нить действует сила натяжения Т=4400Н. Необходимо определить максимальное ускорение подъема груза, масса которого равна m=400 кг, подвешенного на этой нити. При этом нить должна сохранить целостность.

Решение

Представив все силы, оказывающие действие на тело, необходимо составить формулу второго закона Ньютона. Тело является материальной точкой, а силы приложены к центру его массы.

Задача 1

Источник: webmath.ru

(bar{T}+mbar{g}=mbar{a})

(bar{T}) является силой натяжения нити.

Проекция уравнения будет иметь следующий вид:

(T – mg = ma)

Данное выражение позволяет рассчитать ускорение:

(a=frac{T-mg}{m})

Так как все величины, изложенные в задании, соответствуют единицам СИ, можно провести корректные вычисления

(a=frac{4400-4*9,8}{400})

Ответ: a = 1.2 (м/с^2)

Задание 2

На иллюстрации изображен шар, который обладает массой m=0.1 кг. Будучи зафиксирован на нити, шарик совершает движение по окружности в горизонтальной плоскости. Длина подвеса составляет l=5 м, а радиус окружности – R=3 м. Требуется вычислить модуль силы натяжения нити.

Решение

Необходимо воспользоваться вторым законом Ньютона и записать его для сил, которые действуют на шар. Центростремительное ускорение при его вращении по окружности будет записано следующим образом:

(bar{T}+mbar{g}=mbar{a})

Задача 2

Источник: webmath.ru

Проекции данной формулы по осям определяются следующим образом:

X: (T sin α = ma = mω2R)

Y: (-mg + T cos α = 0)

Таким образом, из уравнения Y получаем расчет модуля силы натяжения нити:

(T=frac{mg}{cos alpha })

Анализ рисунка позволяет вывести следующее уравнение:

(sin alpha = frac{R}{l}rightarrow cos alpha = sqrt{1-left(frac{R}{l} right)^{2}})

Если cos α заменить уравнением для расчета модуля силы натяжения нити, то получим следующую формулу:

(T=frac{mg}{sqrt{1-left(frac{R}{l} right)^{2}}}= frac{mgl}{sqrt{l^{2}-R^{2}}})

Значения основных величин, выраженные в СИ, можно подставить в конечную формулу для расчета силы натяжения нити:

(T=frac{0,1*9,8*5}{sqrt{5^{2}-3^{2}}}=1,225left(H right))

Ответ: Т=1,225 H

Источник

Содержание:

Определение и формула силы натяжения нити
Единицы измерения силы натяжения нити
Примеры решения задач

Определение и формула силы натяжения нити

Определение

Силу натяжения определяют как равнодействующую сил $(bar{R})$, приложенных к нити, равную ей по модулю,
но противоположно направленную. Устоявшегося символа (буквы), обозначающего силу натяжения нет. Ее
обозначают и просто $bar{F}$ и
$bar{T}$, и
$bar{N}$ . Математически определение для силы натяжения нити можно записать как:

$$bar{T}=-bar{R}(1)$$

где $bar{R}$ = векторная сумма всех сил, которые действуют на нить. Сила натяжения нити всегда направлена по нити (или подвесу).

Чаще всего в задачах и примерах рассматривают нить, массой которой можно пренебречь. Ее называют невесомой.

Еще одним важной характеристикой нити при расчете силы натяжения является ее растяжимость. Если исследуется невесомая и нерастяжимая
нить, то такая нить считается просто проводящей через себя силу. В том случае, когда необходимо учитывать растяжение нити, применяют
закон Гука, при этом:

$$T=F_{u p r}=k Delta l(2)$$

где k – коэффициент жесткости нити, $Delta l$ – удлинение нити при растяжении.

Единицы измерения силы натяжения нити

Основной единицей измерения силы натяжения нити (как и любой силы) в системе СИ является: [T]=Н

В СГС: [T]=дин

Примеры решения задач

Пример

Задание. Невесомая, нерастяжимая нить выдерживает силу натяжения T=4400Н. С каким максимальным ускорением
можно поднимать груз массой m=400 кг, который подвешивают на эту нить, чтобы она не разорвалась?

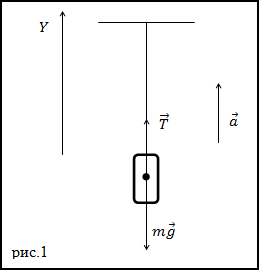
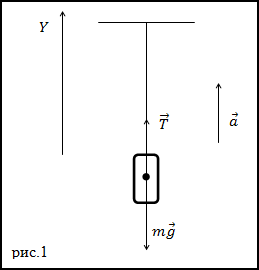
Решение. Изобразим на рис.1 все силы, действующие на груз, и запишем второй закон Ньютона.
Тело будем считать материальной точкой, все силы приложенными к центру масс тела.

$$bar{T}+m bar{g}=m bar{a}(1.1)$$

где $bar{T}$ – сила натяжения нити. Запишем проекцию уравнения (1.1) на ось Y:

$$T-m g=m a(1.2)$$

Из выражения (1.2) получим ускорение:

$$a=frac{T-m g}{m}$$

Все данные в задаче представлены в единицах системы СИ, проведем вычисления:

$$a=frac{4400-400 cdot 9,8}{400}=1,2 mathrm{~m} / mathrm{c}^{2}$$

Ответ. a=1,2м/с²

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Шарик, имеющий массу m=0,1 кг прикрепленный к нити (рис.2) движется по окружности,
расположенной в горизонтальной плоскости. Найдите модуль силы натяжения нити, если длина нити l=5 м, радиус окружности R=3м.

Решение. Запишем второй закон Ньютона для сил, приложенных к шарику, который вращается по окружности с
центростремительным ускорением:

$$bar{T}+m bar{g}=m bar{a}(2.1)$$

Найдем проекции данного уравнения на обозначенные на рис.2 оси X и Y:

$$
begin{array}{c}
X: quad T sin alpha=m a=m omega^{2} R(2.2) \
Y: quad-m g+T cos alpha=0
end{array}
$$

Из уравнения (2.3) получим формулу для модуля силы натяжения нити:

$$T=frac{m g}{cos alpha}(2.4)$$

Из рис.2 видно, что:

$$sin alpha=frac{R}{l} rightarrow cos alpha=sqrt{1-left(frac{R}{l}right)^{2}}$$

Подставим (2.5) вместо $cos alpha$ в выражение (2.4), получим:

$$T=frac{m g}{sqrt{1-left(frac{R}{l}right)^{2}}}=frac{m g l}{sqrt{l^{2}-R^{2}}}$$

Так как все данные в условиях задачи приведены в единицах системы СИ, проведем вычисления:

$$T=frac{0,1 cdot 9,8 cdot 5}{sqrt{5^{2}-3^{2}}}=1,225(H)$$

Ответ. T=1,225 Н

Читать дальше: Формула силы тяги.

Источник

Как определить силу натяжения нити между двумя телами

Содержание:

Сила натяжения нити — основные понятия, обозначение, единица измерения
Как определить для разных условий, формулы для расчета
- Определение силы натяжения на одной нити
- Нахождение силы натяжения на нескольких нитях
Примеры решения задач

Сила натяжения нити — основные понятия, обозначение, единица измерения

Сила натяжения — сила, которую прикладывают к концам объекта, она создает внутри объекта упругую деформацию.

Длина тела, к которому прилагают силу, обычно во много раз больше, чем толщина этого тела. Такими телами могут быть обыденные вещи — канат, веревка, трос, проволока, леска и т. д.

Приведем примеры силы натяжения нити в быту:

применение отвеса для строительства;
установка растяжек для того, чтобы зафиксировать радиоантенны;
характер арматуры внутри напряженного бетона;
устройство такелажа корабля.

Фото такелажа:

Источник: rusgvozdi.ru

Сила натяжения нити является суммой сил, которые действуют на нить, а также противоположна по своему направлению.

F=-F

Здесь F — сила натяжения. Также встречаются обозначения силы натяжения нити с помощью букв «T» и «N». За единицу измерения у силы натяжения нити принимают Ньютон (сокращенно — H).

Как определить для разных условий, формулы для расчета

Существует множество разных вариантов определения силы напряжения нити. Рассмотрим некоторые из них.

Определение силы натяжения на одной нити

Определение силы натяжения на одной нити происходит в несколько этапов.

Первый этап — нужно определить силы на обоих концах нити. Сила натяжения этой нити или веревки считается результатом сил, которые натягивают веревку с каждого из концов.

Напомним, что сила будет равна произведению массы m на ускорение a.

Предположим, что веревка туго натянута. Каждое изменение массы или ускорения объекта, который подвешен на веревке, приведет к тому, что силы на самой веревке изменятся. Не стоит забывать также о постоянном ускорении силы тяжести. Учитывать его нужно даже тогда, когда система остается в покое, а составляющие системы являются объектами воздействия силы тяжести.

Формула 1

Можно сделать предположение, что сила натяжение этой веревки будет рассчитываться по следующей формуле: (T=(mtimes{g})+(mtimes{a})). В данной формуле (g) будет ускорением силы тяжести тела, которое поддерживается веревкой, а показатель «a» будет любым иным ускорением, которое действует на тело.

Примечание 1

Для решения большей части физических задач предполагается, что веревка идеальна. То есть, она идеально тонкая, у нее нет массы, она не способна рваться и растягиваться.

Пример 1

Рассмотрим пример, в котором груз подвешивается к деревянной балке при помощи одной веревки. Ни веревка, и груз не передвигаются — система в абсолютном покое. Чтобы груз находился в полном равновесии, сила натяжения обязана равняться силе тяжести: (F_{т}=F_{g}=mtimes{g}). Если у груза масса 10 кг, то сила натяжения будет равна (98 Н (10times9,8)).

Второй этап — нужно учитывать ускорение. Сила тяжести является не единственной силой, которая может повлиять на силу натяжения нити. Ровно такое же действие совершает каждая сила, которую прикладывают к объекту на нити с ускорением.

Пример 2

Если объект, который подвешен на кабеле или веревке, ускоряется под воздействием силы, то к силе натяжения будет добавляться сила ускорения. Представим, что на веревку подвешивают груз с массой в 10 кг, потом тянут вверх с ускорением, которое равно 1 м/с². В данном случае нужно учитывать ускорение груза вместе с ускорением силы тяжести:

(F=F+(mtimes{a}))

(F=98+(10times{1}))

(F=108 Н.)

Третий этап — нужно учитывать угловое ускорение. Тело находится на веревке, которая вращается вокруг определенной точки, ее считают условным центром (по типу маятника). Оно оказывает натяжение на нить при помощи центробежной силы.

Центробежная сила — побочная сила натяжения, вызванная веревкой. Возникает при толчке внутрь веревки таким образом, чтобы груз сохранял свое движение по дуге, а не по прямой. Центробежная сила тем больше, чем быстрее движется объект: (F=mfrac{v^{2}}{r}.)

В этой формуле m является массой, v — скоростью, r — радиусом окружности, по которой происходит движение груза.

Так как значение и направление центробежной силы изменяются в зависимости от того, как тело передвигается и изменяет собственную скорость, полное натяжение нити становится параллельным нити в центральной точке.

Важно запомнить, что сила притяжения всегда воздействует на тело, тянет его вниз. Если объект совершает амплитудное действие вертикально, полное натяжение сильнее всего будет в нижней точке дуги (точка равновесия для маятника) — когда тело достигает самой большой скорости, а слабее всего — в верхней точке дуги, когда тело начинает замедляться.

Пример 3

Приведем пример: объект не ускоряется вверх, а раскачивается как маятник. Допустим, что нить будет иметь длину 1,5 м, а груз передвигается со скоростью 2 м/с (в случае прохождения через нижнюю точку размаха). Если необходимо рассчитать силу натяжения в нижней точке дуги (в момент, когда она самая большая), то нужно найти сначала, какое давление силы тяжести ощущает на себе груз в данной точке (в состоянии покоя — 98 Н). Для нахождения центробежной силы нужно применить следующие формулы:

(F=mfrac{v^{2}}{r})

(F=10frac{2^{2}}{1,5})

(F=10times2,67=26,7 Н.)

Так полное натяжение нити будет (98+26,7=124,7 Н.)

Еще одна формула — сила натяжения способна изменяться по мере того, как проходит груз по дуге. Величина и направление центробежной силы изменяются по мере того, как тело качается. Даже если сила тяжести постоянная, результирующая сила натяжения изменяется. В тот момент, когда качающееся тело располагается не в нижней точке дуги, сила тяжести тащит тело вниз, однако сила натяжения тянет тело вверх под углом. По данной причине сила натяжения обязана находиться в противодействии лишь части силы тяжести, а не всей.

Деление силы гравитации на два вектора может помочь визуально показать данное состояние. В каждой точке дуги объекта, который раскачивается вертикально, нить создает угол (ominus) с линией, проходящей через точку равновесия, центр вращения. После того как маятник раскачивается, сила гравитации разделяется на два вектора:

(mgsinominus), воздействует по касательной к дуге по направлению к точке равновесия;
(mgcosominus), воздействует параллельно силе натяжения, однако в ином направлении.

Натяжение имеет возможность противостоять (mgcosominus)— только такой силе, которая направлена против нее, а не полноценной силе тяготения (кроме точки равновесия).

Пример 4

Представим пример: маятник имеет отклонение в 15° от вертикали, движение происходит со скоростью 1,5 м/с. Можно найти силу натяжения следующим образом:

Найдем отношение силы натяжения к силе тяготения: (Т=98cos15=98(0,96)=94,08 Н).
Найдем центробежную силу: (F=10timesfrac{1,5^{2}}{1,5}=10times1,5=15).
Полное натяжение будет следующим: (T + F = 94,08 + 15 = 109,08 Н).

Еще одна формула — с учетом расчета трения. Каждый объект, который тянут нитью по поверхности, чувствует на себе силу замедления из-за трения, и передает данное воздействие натяжению в нити.

Сила трения между двумя телами рассчитывается, как и в другой любой ситуации, в соответствии со следующим уравнением: (F=(mu)N). В данной формуле (mu) является коэффициентом силы трения между телами, N является силой взаимодействия двух объектовсила, с которой они воздействуют друг на друга.

Примечание 2

Трение покоя — трение, возникающее в итоге попыток привести тело, находящееся в состоянии покоя, в движение.

Трение движения — трение, которое возникает в итоге попыток заставить движущееся тело продолжать это движение.

Приведем пример: представим, что груз в 10 кг не раскачивается, его тянут по горизонтальной плоскости при помощи нитиверевки. Коэффициент трения по земле будет равен 0,5. Груз передвигается со скоростью, которая постоянна, однако нужно придать телу ускорение в 1 м/с².

Нужно сделать следующие расчеты: (F=10times9,8 =98 Н.)

Сила трения будет рассчитана по формуле: (F=0,5times98=49 Н.)

Сила ускорения будет рассчитана по формуле: (F=10times1=10 Н).

Общее натяжение: (F+F=49+10=59 Н.)

Нахождение силы натяжения на нескольких нитях

Один из способов нахождения силы натяжения нити — использовать вертикальные параллельные грузы при помощи блока.

Блок — простой механизм, который состоит из подвесного диска. Это помогает ему изменять направление силы натяжения веревки.

В обычном расположении блока кабельнитьверевка начинаются от подвешенного объекта вверх к блоку, потом вниз к иному объекту. Так создаются два разных участка веревки. В таком случае натяжение на всех участках становятся одинаковыми, если оба конца натягиваются силами различных величин.

Для системы масс, подвешенных вертикально в блоке, сила натяжения будет равна (T=frac{2g(m1)(m2)}{m2+m1)}). В данной формуле g будет ускорением силы тяжести, m1 — массой первого тела, m2 — массой второго тела.

Примечание 3

Во многих физических задачах блоки являются идеальными — не обладают массой, трением, не ломаются, не отделяются от нити, не деформируются.

Приведем пример: есть два груза, которые подвешены через блок на параллельных концах нити. Один груз обладает массой в 10 кг, а второй груз обладает массой в 5 кг. В данном случае нужно произвести расчет по следующим формулам:

(T=frac{2g(m1)(m2)}{m2+m1)})

(T=frac{2(9,8)(10)(5)}{5+10)}=frac{980}{15}=65,33 Н.)

Важно понимать, что из-за того, что один груз является более тяжелым, другие элементы будут равны, данная система будет ускоряться, значит, груз в 10 кг будет передвигаться вниз, заставляя второй объект идти вверх.

Другая формула — подвешиваем грузы, берем блоки с нитями, которые не параллельны. Блоки часто используют для того, чтобы направить силу натяжения в другую сторону. Если груз подвешивается вертикально к одному концу нити, а другой конец поддерживает груз в диагональной плоскости, то система блоков — непараллельная — формирует треугольную форму с углами в точках с первым грузом, вторым, а также самим блоком. В данном случае натяжение в веревке будет зависеть от силы тяжести, силы натяжения, которая будет параллельная диагональной части нити.

Пример 5

Приведем пример: есть система с объектом в 10 кг, подвешенным вертикально, соединяющимся с грузом в 5 кг, который находится на наклонной плоскости в 60° (нет трения). Для нахождения натяжения в нити нужно составить следующие уравнения:

Груз, который подвешивают, намного тяжелее, трение не создается, потому что мы знаем, что груз ускоряется вниз. Натяжение в веревке тащит вверх, поэтому объект ускоряется по отношению к силе (равнодействующей) (F=m1times{g}-T=98-Т.)
Груз на плоскости, которая находится под наклоном, ускоряется вверх. Так как трения нет у данной плоскости, натяжение тянет груз вверх по плоскости, вниз объект тянет собственный вес. Часть силы, которая тянет вниз по наклонной, будет вычисляться как (mgsinominus). Можно предположить, что тело ускоряется по отношению к равнодействующей силе: (F=T-m^{2}(g)sin60=T-5(9,8)(0,87)=T-42,14).
Если сравнять оба уравнения, то получится следующее: (98-T=T-42,12). Вычисляем T, получается, что (2T=140,14. Так T=70,07 )Н.

Последняя формула — использование нескольких нитей для того, чтобы подвесить тело. Представим, что объект подвешивается на «Y-образной» системе нитей — две нити закрепляются на потолке, встречаются в центральной точке, из которой третья нить идет с объектом. Сила натяжения третьей нити проста — обычное натяжение в итоге действия силы тяжести или же m(g).

Натяжение на других нитях отличается, они обязаны составлять в совокупности силу, которая равна силе тяжести вверх в вертикальном положении, а также равны нулю в обоих горизонтальных направлениях. Однако нужно взять во внимание, что система покоится. Натяжение в нити зависит напрямую от массы подвешенных грузов, а также от угла, на который происходит наклон каждой нити от потолка.

Пример 6

Приведем пример: в системе Y-образной нижний груз обладает массой в 10 кг, подвешивается на двух нитях, угол одной из нитей составляет 30° с потолком. Угол второй нити составляет 60°. Если необходимо найти натяжение каждой нити, необходимо рассчитать вертикальную и горизонтальную части натяжения. Для того чтобы найти T1 (натяжение с наклоном в 30°), T2 (натяжение с наклоном в 60°), нужно рассчитать:

По законам тригонометрии, соотношение между T=m(g) и Т1, Т2 будет равно косинусу угла между нитями и потолком. Для натяжения T1 будет (cos30=0,87). Для натяжения T2 будет (cos60=0,5).
Нужно умножить натяжение в нижней нити на косинус всех углов, чтобы найти общее натяжение. (T1=0,87times{mg}=0,87times10(9,8)=85,26) Ньютонов. (T2=0,5times{mg}=0,5times10(9,8)=49) Ньютонов.

Примеры решения задач

Задача

Нерастяжимая, с малым весом нить может выдержать силу натяжения в T=4400 Н. Какое максимальное ускорение может быть, чтобы поднять груз с массой в 400 кг? Груз подвешивают на данную нить. Нужно, чтобы нить при этом не разорвалась, и не произошло падение груза.

На рисунке ниже изображены все силы, которые воздействуют на груз.

Запишем второй закон Ньютона. Объект считается материальной точкой, все силы прикладываются к центру масс объекта: (T+mg=ma).

Далее записываем проекции уравнения на ось Y: (T-mg=ma).

Получаем уравнение: (a=frac{T-mg}{m}).

Произведем расчеты: (a=frac{4400-400times9,8}{400}=1,2 м/с²).

Ответ: 1,2 м/с².

Источник

1
сила натяжения

Универсальный русско-английский словарь > сила натяжения
2
сила натяжения

Русско-английский физический словарь > сила натяжения
3
сила натяжения

Русско-английский исловарь по машиностроению и автоматизации производства > сила натяжения
4
сила натяжения

Русско-английский словарь по химии > сила натяжения
5
сила натяжения

Русско-английский словарь по микроэлектронике > сила натяжения
6
сила натяжения

Русско-английский научно-технический словарь Масловского > сила натяжения
7
сила натяжения

Русско-английский политехнический словарь > сила натяжения
8
сила натяжения

Большой русско-английский медицинский словарь > сила натяжения
9
сила натяжения каната

Универсальный русско-английский словарь > сила натяжения каната
10
сила натяжения на тросах

Универсальный русско-английский словарь > сила натяжения на тросах
11
сила натяжения нити

Универсальный русско-английский словарь > сила натяжения нити
12
сила натяжения провода

Универсальный русско-английский словарь > сила натяжения провода
13
сила натяжения пружины

Универсальный русско-английский словарь > сила натяжения пружины
14
Сила натяжения струны

Русско-английский словарь по прикладной математике и механике > Сила натяжения струны
15
номинальная сила натяжения пружины

Универсальный русско-английский словарь > номинальная сила натяжения пружины
16
сила

ж.

force; strength

— адгезионная сила
— активная сила
— архимедова сила
— аэродинамическая подъёмная сила при дозвуковых скоростях
— аэродинамическая подъёмная сила при околозвуковых скоростях
— аэродинамическая подъёмная сила при сверхзвуковых скоростях
— аэродинамическая подъёмная сила
— аэродинамическая сила в колеблющемся потоке
— аэродинамическая сила
— аэростатическая подъёмная сила
— близкодействующая сила
— боковая аэродинамическая сила
— боковая сила
— валентная сила
— ван-дер-ваальсовы силы
— вертикальная сила
— взаимодействующая сила
— вибродвижущая сила
— внецентренная сила
— внешняя сила
— внутренняя сила
— внутриатомные силы
— внутриядерные силы
— возбуждающая сила
— возвращающая сила
— возмущающая сила
— восстанавливающая сила
— вращающая сила
— всасывающая сила
— вынуждающая сила
— выталкивательная сила
— выталкивающая сила
— гармоническая сила
— гигантская сила осциллятора
— гидродинамическая подъёмная сила
— гидродинамическая сила
— гидростатическая подъёмная сила
— гиперон-ядерные силы
— гироскопическая сила
— гравимагнитная сила
— гравитационная сила
— дальнодействующая сила
— движущая сила трещины
— движущая сила
— двухчастичная сила
— демпфирующая сила
— деформирующая сила
— динамическая сила
— диполь-дипольные ван-дер-ваальсовы силы
— диполь-квадрупольная сила
— дипольная сила осциллятора
— дисперсионные силы
— диссипативная сила
— диссоциирующая сила
— заданная сила
— задерживающая сила
— закручивающая сила
— замедляющая сила
— зарядово-независимая сила
— засасывающая сила
— знакопеременная сила
— избыточная подъёмная сила
— изгибающая сила
— импульсная сила
— индуцированная подъёмная сила
— инерционная сила
— ионная сила
— кажущаяся подъёмная сила
— капиллярные силы
— касательная аэродинамическая сила
— касательная сила
— квадрупольная сила
— квадрупольные ван-дер-ваальсовы силы
— квазиупругая сила
— когезионная сила
— консервативная сила
— контурная сила
— копланарные силы
— кориолисова сила
— короткодействующая сила
— коэрцитивная сила
— критическая сила при продольном изгибе
— критическая сила
— крутящая сила
— кулоновская сила
— линейная сила голограммы
— линейная сила
— лошадиная сила
— магнитодвижущая сила
— майорановская обменная сила
— массовая сила
— мгновенная сила
— межатомные силы
— межмолекулярные силы
— межнуклонная сила
— механическая подъёмная сила
— механическая сила
— многочастичная сила
— многочастичные ван-дер-ваальсовы силы
— молекулярные силы
— мультиполь-мультипольные ван-дер-ваальсовы силы
— мультипольная сила
— мультипольные ван-дер-ваальсовы силы
— наведённая электродвижущая сила
— намагничивающая сила
— направляющая сила
— недиссипативная сила
— неконсервативная сила
— некопланарные силы
— нелинейная возвращающая сила
— нелинейная сила
— непотенциальная сила
— неравномерно распределённая подъёмная сила
— неуравновешенная сила
— нецентральная сила
— номинальная сила
— нормальная аэродинамическая сила
— нормальная сила
— нулевая подъёмная сила
— ньютоновская сила тяготения
— обменная сила
— обобщённая сила осциллятора
— обобщённая сила
— объёмная пондеромоторная сила
— объёмная сила
— ограничивающая сила
— одновременно действующие силы
— опрокидывающая сила, действующая на катушку тороидального магнитного поля
— оптическая сила линзы
— осевая сила
— отклоняющая сила
— отрицательная подъёмная сила
— отрицательная сила осциллятора
— переменная сила
— переносная сила инерции
— периодическая возмущающая сила
— периодическая сила
— периодически действующая сила
— поверхностная сила
— подсасывающая сила
— подъёмная сила в восходящем потоке нагретого воздуха
— подъёмная сила в неравномерном потоке
— подъёмная сила крыла
— подъёмная сила на единицу размаха
— подъёмная сила от реактивной струи
— подъёмная сила при неустановившемся обтекании
— подъёмная сила при околозвуковых скоростях
— подъёмная сила тонкого крыла
— подъёмная сила
— подъёмная сила, приложенная к поверхности
— подъёмная сила, распределённая по поверхности
— полная подъёмная сила
— пондеромоторная сила
— поперечная аэродинамическая сила
— поперечная сила трения
— поперечная сила
— постоянная сила
— потенциальная сила
— приведённая сила
— прижимающая сила
— приливные силы
— приливообразующая сила
— приложенная сила
— продольная сила трения
— противодействующая сила
— противоэлектродвижущая сила
— псевдогравитационная сила
— пульсирующая сила
— равнодействующая сила
— равномерно распределённая сила
— радиальная сила
— радиационная сила
— размагничивающая сила
— разрешающая сила
— разрушающая сила
— расклинивающая сила
— распределённая сила
— растягивающая сила
— расчётная подъёмная сила
— расчётная сила
— расширяющая сила
— реактивная сила
— результирующая подъёмная сила
— результирующая сила реакции
— результирующая сила
— релаксационная коэрцитивная сила
— сверхобменная сила
— сдвигающая сила
— сжимающая сила
— сила Абрагама
— сила адгезии
— сила Ампера
— сила Архимеда
— сила Бернулли
— сила Бьеркнеса
— сила ветра
— сила взаимодействия
— сила Вигнера
— сила внутреннего трения
— сила внутрикристаллической связи
— сила вязкого сопротивления
— сила голограммы
— сила давления текущей жидкости на шар
— сила давления
— сила динамического давления
— сила дисклинации
— сила звука
— сила землетрясения
— сила земного притяжения
— сила излучения
— сила инерции вращающихся масс
— сила инерции
— сила Казимира
— сила кинетического трения
— сила когезии
— сила Кориолиса
— сила линии
— сила лобового сопротивления
— сила Лоренца
— сила магнита
— сила магнитного давления
— сила магнитного натяжения
— сила Миллера
— сила натяжения
— сила ньютоновского тяготения
— сила осциллятора при излучении
— сила осциллятора при поглощении
— сила осциллятора
— сила отдачи
— сила отталкивания
— сила Пайерлса — Набарро
— сила Пайерлса
— сила пиннинга
— сила плавучести
— сила поверхностного натяжения
— сила поверхностного трения
— сила притяжения
— сила противодействия
— сила разгруппирования
— сила реакции
— сила Розенфельда
— сила сверхсильного взаимодействия
— сила сверхслабого взаимодействия
— сила света
— сила связи
— сила сжатия
— сила слабого взаимодействия
— сила сопротивления для медленно движущегося произвольного трёхмерного эллипсоида
— сила сопротивления при потенциальном обтекании тела
— сила сопротивления
— сила сопротивления, действующая на произвольно движущийся шар
— сила сопротивления, отнесённая к единице длины цилиндра
— сила столкновения для оптически разрешённого перехода
— сила столкновения
— сила сцепления
— сила тока
— сила торможения
— сила трения в пограничном слое
— сила трения движения
— сила трения качения
— сила трения между тяжёлыми и лёгкими ионами
— сила трения покоя
— сила трения
— сила трения, действующая на стенку
— сила трения, связанная с краевыми эффектами
— сила тяги
— сила тяготения
— сила тяжести
— сила удара
— сила упругости
— сила электромагнитного взаимодействия
— сила электростатического притяжения
— сила, действующая на переднюю кромку
— сила, действующая на соприкасающуюся с жидкостью твёрдую поверхность
— сила, зависящая от скорости
— сила, зависящая от энергии
— сила, направленная вверх
— сила, направленная вниз
— сила, направленная вперёд
— сила, направленная назад
— сила, перпендикулярная скорости течения
— силы Ван-дер-Ваальса
— силы с пересекающимися линиями действия
— следящая сила
— согласованная сила
— сосредоточенная сила
— составляющая сила
— средняя по времени сила
— средняя сила
— средняя сферическая сила света
— статическая подъёмная сила
— статическая сила
— стационарная сила
— сторонние силы
— стохастическая сила
— суммарная подъёмная сила
— суммарная сила
— тангенциальная сила
— тензорная сила
— термокапиллярная сила
— термофоретическая сила
— термоэлектродвижущая сила
— тормозящая сила
— трёхчастичная сила
— трёхчастичные ван-дер-ваальсовы силы
— трещинодвижущая сила
— ударная сила
— удельная сила трения
— удерживающая сила
— упругая сила
— уравновешенная сила
— уравновешивать силы
— уравновешивающая сила
— ускоряющая сила
— усреднённая сила столкновения
— фактическая подъёмная сила
— фотоэлектродвижущая сила
— фундаментальная сила
— цветная сила
— центральная предельная сила
— центральная сила
— центробежная сила
— центростремительная сила
— циркуляционная подъёмная сила
— эквивалентная сила
— экранированная сила
— электродвижущая сила
— электрокинетическая сила
— электрослабая сила
— электростатические силы
— элементарная сила давления
— энергетическая сила света
— ядерные силы

Русско-английский физический словарь > сила
17
сила поверхностного натяжения

Русско-английский новый политехнический словарь > сила поверхностного натяжения
18
сила

1. bulwark

2. effect

3. energy

4. greatness

5. vigor

6. vigour

7. vim

8. pitch

9. virtue

благодаря; посредством; в силу; на основании — by virtue of

10. force of

11. potency

12. strengths

13. violence

14. strength; force; power; might; vigour; intensity; efficacy; energy; volume

15. drive

16. force

17. intensity

18. power

19. vehemence

20. volume

Синонимический ряд:

1. множество (сущ.) бездна; вагон; воз; гибель; гора; куча; масса; множество; море; пропасть; прорва; тьма; тьма тем; тьма-тьмущая; уймища

2. мочь (сущ.) мочь

3. мощь (сущ.) могущество; мощность; мощь

4. насилие (сущ.) насилие

Антонимический ряд:

бессилие; слабость

Русско-английский большой базовый словарь > сила
19
сила

Большой русско-английский медицинский словарь > сила
20
сила

Русско-английский автомобильный словарь > сила

Страницы

См. также в других словарях:

сила натяжения — įtempimo jėga statusas T sritis Standartizacija ir metrologija apibrėžtis Deformuojamame kūne atsirandanti vidinė jėga. atitikmenys: angl. strain force; tension force vok. Spannkraft, f rus. сила натяжения, f; сила растяжения, f pranc. force de… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
сила натяжения — įtempimo jėga statusas T sritis Standartizacija ir metrologija apibrėžtis Kūną tempianti ar spaudžianti jėga. atitikmenys: angl. strain force; tension force vok. Spannkraft, f rus. сила натяжения, f; сила растяжения, f pranc. force de tension, f; … Penkiakalbis aiškinamasis metrologijos terminų žodynas
сила натяжения — įtempimo jėga statusas T sritis fizika atitikmenys: angl. strain force; tension force vok. Spannkraft, f rus. сила натяжения, f; сила растяжения, f pranc. force de tension, f; force tensionnelle, f … Fizikos terminų žodynas
сила натяжения — tempimo jėga statusas T sritis fizika atitikmenys: angl. tension force vok. Spannungskraft, f rus. сила натяжения, f pranc. force de tension, f; force tensionnelle, f … Fizikos terminų žodynas
СИЛА — силы, ж. 1. Способность живых существ производить физические действие, энергия, порождаемая способностью управлять движениями мышц. «Какой то муравей был силы непомерной…» Крылов. «Пригожеством, ростом и силой ты ровни в селе не имел.» Некрасов.… … Толковый словарь Ушакова
СИЛА — (Force) причина, сообщающая телу ускорение, т. е. заставляющая тело выйти из состояния покоя или изменяющая скорость или направление его движения. Механика совершенно отвлекается от физической природы этой причины; сила притяжения земли, сила… … Морской словарь
Сила — Запрос «сила» перенаправляется сюда; см. также другие значения. Сила Размерность LMT−2 Единицы измерения СИ ньютон … Википедия
Сила (физическая величина) — Запрос «сила» перенаправляется сюда; см. также другие значения. Сила Размерность LMT−2 Единицы измерения СИ … Википедия
сила растяжения — įtempimo jėga statusas T sritis Standartizacija ir metrologija apibrėžtis Deformuojamame kūne atsirandanti vidinė jėga. atitikmenys: angl. strain force; tension force vok. Spannkraft, f rus. сила натяжения, f; сила растяжения, f pranc. force de… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
сила растяжения — įtempimo jėga statusas T sritis Standartizacija ir metrologija apibrėžtis Kūną tempianti ar spaudžianti jėga. atitikmenys: angl. strain force; tension force vok. Spannkraft, f rus. сила натяжения, f; сила растяжения, f pranc. force de tension, f; … Penkiakalbis aiškinamasis metrologijos terminų žodynas
сила растяжения — įtempimo jėga statusas T sritis fizika atitikmenys: angl. strain force; tension force vok. Spannkraft, f rus. сила натяжения, f; сила растяжения, f pranc. force de tension, f; force tensionnelle, f … Fizikos terminų žodynas

Источник

Склонение существительного «натяжение»

Существительное «натяже́ние» (неод.)

Падеж	Единственное число	Множественное число
Именительный Кто? Что?	натяже́ние	натяже́ния
Родительный Кого? Чего?	натяже́ния	натяже́ний
Дательный Кому? Чему?	натяже́нию	натяже́ниям
Винительный (неод.) Кого? Что?	натяже́ние	натяже́ния
Творительный Кем? Чем?	натяже́нием	натяже́ниями
Предложный О ком? О чём?	натяже́нии	натяже́ниях

Делаем Карту слов лучше вместе

Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать
Карту слов. Я отлично
умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!

Спасибо! Я стал чуточку лучше понимать мир эмоций.

Вопрос: эзоповский — это что-то нейтральное, положительное или отрицательное?

Ассоциации к слову «натяжение»

Синонимы к слову «натяжение»

Предложения со словом «натяжение»

Сила поверхностного натяжения воды настолько велика, что может удерживать предметы, которые, казалось бы, плавать не должны.
То есть, если струны цепляют гриф, и он визуально выгнут в противоположную направлению силы натяжения струн сторону, – скорее всего, что анкер просто перетянут, и его нужно ослабить.
После настройки инструмента снова проверяем прогиб, и если опять требуется регулировка, – ослабляем натяжение струн, и производим повторную регулировку.
(все предложения)

Цитаты из русской классики со словом «натяжение»

Все двигаются не торопясь и молча, а он вертится около головки — у колеса, щупает чёрными пальцами натяжение струн, приседая, смотрит узкими глазами вдоль них и бежит на прямых ногах в конец пустыря, чтобы облегчить или прибавить груз.
(все
цитаты из русской классики)

Каким бывает «натяжение»

Значение слова «натяжение»

НАТЯЖЕ́НИЕ, -я, ср. 1. Действие по глаг. натянуть—натягивать (в 1 знач.) и состояние по глаг. натянуться—натягиваться (в 1 знач.). Отрегулировать натяжение пилы. Степень натяжения струн. (Малый академический словарь, МАС)

Все значения слова НАТЯЖЕНИЕ

Отправить комментарий

Дополнительно

Смотрите также

НАТЯЖЕ́НИЕ, -я, ср. 1. Действие по глаг. натянуть—натягивать (в 1 знач.) и состояние по глаг. натянуться—натягиваться (в 1 знач.). Отрегулировать натяжение пилы. Степень натяжения струн.

Все значения слова «натяжение»

Сила поверхностного натяжения воды настолько велика, что может удерживать предметы, которые, казалось бы, плавать не должны.
То есть, если струны цепляют гриф, и он визуально выгнут в противоположную направлению силы натяжения струн сторону, – скорее всего, что анкер просто перетянут, и его нужно ослабить.
После настройки инструмента снова проверяем прогиб, и если опять требуется регулировка, – ослабляем натяжение струн, и производим повторную регулировку.
(все предложения)

сращение
срастание
сращивание
натяжка
натягивание
(ещё синонимы…)

тетива
потолок
натяг
натянуть
притяжение
(ещё ассоциации…)

поверхностное натяжение
натяжение верёвки
сила натяжения
натяжение ослабло
ослабить натяжение
(полная таблица сочетаемости…)

поверхностное
первичное
вторичное
чрезмерное
сильное
(ещё…)

Склонение
существительного «натяжение»
Разбор по составу слова «натяжение»

Как правильно пишется слово «натяжение»

Источник

На букву С Со слова «сила»

Фраза «сила натяжения»

Фраза состоит из двух слов и 13 букв без пробелов.