Как пишется знак разность - Napishi.top - правописание и грамматика

{} набор набор элементов A = {3,7,9,14},
B = {9,14,28} А ∩ Б пересечение объекты, принадлежащие множеству A и множеству B A ∩ B = {9,14} А ∪ Б союз объекты, принадлежащие множеству A или множеству B A ∪ B = {3,7,9,14,28} А ⊆ Б подмножество A является подмножеством B. множество A включено в набор B. {9,14,28} ⊆ {9,14,28} A ⊂ B правильное подмножество / строгое подмножество A является подмножеством B, но A не равно B. {9,14} ⊂ {9,14,28} А ⊄ Б не подмножество множество A не является подмножеством множества B {9,66} ⊄ {9,14,28} А ⊇ Б суперсет A является надмножеством B. множество A включает множество B {9,14,28} ⊇ {9,14,28} А ⊃ Б правильный суперсет / строгий суперсет A является надмножеством B, но B не равно A. {9,14,28} ⊃ {9,14} А ⊅ Б не суперсет множество A не является надмножеством множества B {9,14,28} ⊅ {9,66} 2 ^А набор мощности все подмножества A

набор мощности все подмножества A А = В равенство оба набора имеют одинаковые элементы A = {3,9,14},
B = {3,9,14},
A = B А ^в дополнять все объекты, не принадлежащие множеству A А Б относительное дополнение объекты, принадлежащие A, а не B A = {3,9,14},
B = {1,2,3},
AB = {9,14} А — Б относительное дополнение объекты, принадлежащие A, а не B A = {3,9,14},
B = {1,2,3},
AB = {9,14} A ∆ B симметричная разница объекты, принадлежащие A или B, но не их пересечение A = {3,9,14},
B = {1,2,3},
A ∆ B = {1,2,9,14} А ⊖ Б симметричная разница объекты, принадлежащие A или B, но не их пересечение A = {3,9,14},
B = {1,2,3},
A ⊖ B = {1,2,9,14} a ∈A элемент,
принадлежит установить членство A = {3,9,14}, 3 ∈ A x ∉A не элемент нет установленного членства A = {3,9,14}, 1 ∉ A ( а , б ) упорядоченная пара сборник из 2-х элементов A × B декартово произведение множество всех упорядоченных пар из A и B | A | мощность количество элементов множества A A = {3,9,14}, | A | = 3 #A мощность количество элементов множества A A = {3,9,14}, # A = 3 | вертикальная полоса такой, что А = {х | 3 <х <14}

алеф-нуль бесконечная мощность множества натуральных чисел

алеф-он мощность множества счетных порядковых чисел Ø пустой набор Ø = {} C = {Ø}

универсальный набор набор всех возможных значений

₀ набор натуральных / целых чисел (с нулем)

₀ = {0,1,2,3,4, …} 0 ∈

₀

₁ набор натуральных / целых чисел (без нуля)

₁ = {1,2,3,4,5, …} 6 ∈

₁

набор целых чисел

= {…- 3, -2, -1,0,1,2,3, …} -6 ∈

набор рациональных чисел

= { x | x = a / b , a , b ∈

} 2/6 ∈

набор реальных чисел

= { x | -∞ < х <∞} 6.343434∈

набор комплексных чисел

= { z | z = a + bi , -∞ < a <∞, -∞ < b <∞} 6 + 2 i ∈

Источник

В математике повсеместно используются символы для упрощения и сокращения текста. Ниже приведён список наиболее часто встречающихся математических обозначений, соответствующие команды в TeXе, объяснения и примеры использования.

Кроме указанных символов, иногда используются их зеркальные отражения, например, обозначает то же, что и

Знаки операций или математические символы — знаки, которые символизируют определённые математические действия со своими аргументами.

Символ (TeX) Символ (Unicode) Название Значение Пример Произношение Раздел математики

⇒

→

⊃

Импликация, следование

означает «если

верно, то

также верно».
(→ может использоваться вместо ⇒ или для обозначения функции, см. ниже.)
(⊃ может использоваться вместо ⇒, или для обозначения надмножества, см. ниже.).

верно, но

неверно (так как x=-2

также является решением). «влечёт» или «если…, то» везде

⇔ Равносильность

означает «

верно тогда и только тогда, когда

верно».

«если и только если» или «равносильно» везде wedge

∧ Конъюнкция

истинно тогда и только тогда, когда

оба истинны.

, если

— натуральное число. «и» Математическая логика vee

∨ Дизъюнкция Avee B

истинно, когда хотя бы одно из условий

истинно.

(nleqslant 2)vee (ngeqslant 4)Leftrightarrow nne 3

, если

— натуральное число. «или» Математическая логика neg

¬ Отрицание neg A

истинно тогда и только тогда, когда ложно

neg (Awedge B)Leftrightarrow (neg A)vee (neg B)

«не» Математическая логика forall

∀ Квантор всеобщности

обозначает « P(x)

верно для всех

».

«Для любых», «Для всех» Математическая логика exists

∃ Квантор существования

означает «существует хотя бы один

такой, что верно P(x)

(подходит число 5) «существует» Математическая логика

= Равенство x=y

обозначает «

обозначают одно и то же значение». 1 + 2 = 6 − 3 «равно» везде

:⇔

Определение x := y

означает «

по определению равен

».

означает «

по определению равносильно

» ${rm ch} (x) := {1over 2}left(e^x+e^{-x}right)$ (Гиперболический косинус)

A oplus B :Leftrightarrow (Avee B)wedge neg (Awedge B)

(Исключающее или) «равно/равносильно по определению» везде { ,}

{ , } Множество элементов

означает множество, элементами которого являются

(множество натуральных чисел) «Множество…» Теория множеств { | }

{ : }

{ | }

{ : }

Множество элементов, удовлетворяющих условию

означает множество всех

таких, что верно P(x)

. ${nin mathbb N,|,n^2<20} = {1,;2,;3,;4}$ «Множество всех… таких, что верно…» Теория множеств

∅

{}

Пустое множество

означают множество, не содержащее ни одного элемента. ${nin mathbb N,|,1<n^2<4} = varnothing$ «Пустое множество» Теория множеств

notin

∈

∉

Принадлежность/непринадлежность к множеству ain S

означает «

является элементом множества

означает «

не является элементом множества

«принадлежит», «из»
«не принадлежит» Теория множеств

subset

⊆

⊂

Подмножество

означает «каждый элемент из

также является элементом из

».

обычно означает то же, что и

. Однако некоторые авторы используют subset

, чтобы показать строгое включение (то есть

«является подмножеством», «включено в» Теория множеств

⊇

⊃

Надмножество

означает «каждый элемент из

также является элементом из

».

обычно означает то же, что и

. Однако некоторые авторы используют supset

, чтобы показать строгое включение (то есть

«является надмножеством», «включает в себя» Теория множеств

⊊ Собственное подмножество

означает

«является собственным подмножеством», «строго включается в» Теория множеств

⊋ Собственное надмножество

означает

«является собственным надмножеством», «строго включает в себя» Теория множеств cup

∪ Объединение Acup B

означает множество элементов, принадлежащих

или

(или обоим сразу).

«Объединение … и …», «…, объединённое с …» Теория множеств cap

⋂ Пересечение Acap B

означает множество элементов, принадлежащих и

, и

. ${xin R,|,x^2=1}cap mathbb N = {1}$ «Пересечение … и … », «…, пересечённое с …» Теория множеств

Разность множеств

означает множество элементов, принадлежащих

, но не принадлежащих

{1,;2,;3,;4}setminus {3,;4,;5,;6} = {1,;2}

«разность … и … », «минус», «… без …» Теория множеств

→ Функция

означает функцию

с областью определения

и областью прибытия (областью значений)

. Функция

, определённая как

«из … в», везде mapsto

↦ Отображение

означает, что образом

после применения функции

будет

. Функцию, определённую как

, можно записать так:

«отображается в» везде

N или ℕ Натуральные числа

означает множество

или реже

(в зависимости от ситуации).

«Эн» Числа

Z или ℤ Целые числа

означает множество

{a,;-a,|,ainmathbb N} cup { 0 }=mathbb Z

«Зед» Числа

Q или ℚ Рациональные числа

означает

left{left.{pover q} right| pin mathbb Z wedge qin mathbb Zwedge qne 0right}

«Ку» Числа

R или ℝ Вещественные числа, или действительные числа

означает множество всех пределов последовательностей из

(

— комплексное число: i^2=-1

) «Эр» Числа

C или ℂ Комплексные числа

означает множество

«Це» Числа

<
> Сравнение x<y

обозначает, что

строго меньше

означает, что

строго больше

«меньше чем», «больше чем» Отношение порядка

≤ или ⩽
≥ или ⩾ Сравнение

означает, что

меньше или равен

означает, что

больше или равен

«меньше или равно»; «больше или равно» Отношение порядка approx

≈ Приблизительное равенство

с точностью до $10^{-3}$ означает, что 2,718 отличается от

не больше чем на $10^{-3}$ .

с точностью до $10^{-7}$ . «приблизительно равно» Числа sqrt{ }

√ Арифметический квадратный корень sqrt x

означает неотрицательное действительное число, которое в квадрате даёт

$sqrt {x^2}= left|xright|$ «Корень квадратный из …» Числа infty

∞ Бесконечность +infty

суть элементы расширенного множества действительных чисел. Эти символы обозначают числа, меньшее/большее всех действительных чисел. $limlimits_{xto 0} {1over left|xright|}= infty$ «Плюс/минус бесконечность» Числа

| | Модуль числа (абсолютное значение), модуль комплексного числа или мощность множества

обозначает абсолютную величину

обозначает мощность множества

и равняется, если

конечно, числу элементов

. $left|a+bcdot iright|=sqrt {a^2+b^2}$ «Модуль»; «Мощность» Числа и Теория множеств sum

∑ Сумма, сумма ряда $sum_{k=1}^n a_k$ означает «сумма a_k

, где

принимает значения от 1 до

», то есть

.
$sum_{k=1}^{infty} a_k$ означает сумму ряда, состоящего из a_k

. $sum_{k=1}^4 k^2=$

«Сумма … по … от … до …» Арифметика, Математический анализ prod

∏ Произведение $prod_{k=1}^n a_k$ означает «произведение a_k

для всех

от 1 до

», то есть

$prod_{k=1}^4 (k+2)=$

«Произведение … по … от … до …» Арифметика

! Факториал

означает «произведение всех натуральных чисел от 1 до

включительно, то есть

$n! = prod_{k=1}^n k = (n-1)!n$
0! = 1

факториал» Комбинаторика int dx

∫ Интеграл

означает «интеграл от

до

функции

от

по переменной

». $intlimits_0^b x^2, dx = frac{b^3}{3}$
$int x^2, dx = frac{x^3}{3} + C$ «Интеграл (от … до …) функции … по (или d)…» Математический анализ $begin{align} & frac{df}{dx} \ & f'(x), \ end{align}$ df/dx
f'(x) Производная $frac{df}{dx}$ или f'(x)

означает «(первая) производная функции

от

по переменной

». $frac{d cos x}{dx} = -sin x$ «Производная … по …» Математический анализ $begin{align} & frac{d^n f}{dx^n} \ & f^{(n)} (x), \ end{align}$

$f^{(n)}(x)$ Производная

-го порядка $frac{d^n f}{dx^n}$ или $f^{(n)} (x)~$ (во втором случае если

— фиксированное число, то оно пишется римскими цифрами) означает «

-я производная функции

от

по переменной

». $frac{d^4 cos x}{dx^4} = cos x$ «

-я производная … по …» Математический анализ

Источник

Математика – царица наук, а арифметика – царица математики. В повседневной жизни нам часто приходится что-либо считать, а потом и оформлять наши подсчёты в письменном виде. В процессы письменного оформления соотношений величин мы нередко используем знаки «Больше» или «Меньше». При этом многие люди, непосредственно не занятые арифметикой на бумаге, могут со временем позабыть, в какую из сторон (левую или правую) пишутся данные знаки. В нашем материале мы подробно разберём, в какую из сторон пишется знак больше, меньше или равно, и какие приёмы позволят эффектно запомнить изложенную информацию.

Как пишется знак больше меньше в математике
Что значит «меньше или равно»?
Обучение с использованием символов «больше» или «меньше»
Объединение знаков
Ключевые советы по работе с неравенствами
Знаки больше или меньше на клавиатуре
Видео:

Как пишется знак больше меньше в математике

Знаки «больше (>)» или «меньше (<)» обычно используются для отображения отношений между числами. Они позволяют продемонстрировать, какое число имеет большее или меньшее значение, и применяются с целью помочь учащимся разобраться с соотношениями чисел. Знаки «больше» или «меньше» также часто известны как знаки «больше чем» и «меньше чем».

Широкий конец данного знака всегда обращён к большему числу. Например:

25 > 10

100 > 50

500 > 200

Знак «больше» (>) означает, что число перед знаком «больше» всегда больше числа, которое находится после данного знака.

200 > 100

Знак меньше (<) означает, что число перед данным знаком всегда меньше, нежели число после данного знака. Как видим, визуально знак «больше» и «меньше» — это просто перевернутые версии одного и того же символа.

100 < 200

Знак равенства (=) означает, что число после знака равно числу перед знаком.

Важно! Знак равенства не является показателем результата работы над числами (например, 3+5=8). Данный знак показывает, что сумма чисел слева равна сумме чисел справа. То есть 3+5 слева равно числу справа, которым и является 8.

Когда же два значения определенно не равны, тогда мы используем пример со знаком «не равно»: 2+2 ≠ 9. То есть сумма значений чисел слева (4) не равно значению чисел справа (9).

Читайте также: как посчитать разницу в процентах между двумя имеющимися числами.

Что значит «меньше или равно»?

Разобрав, в какую именно сторону пишутся знаки больше, меньше или равно, разберём также ситуации, когда какое-либо значение меньше, но может быть также равно. Например, чайник может вмещать до 10 стаканов воды. Так сколько в нём может быть воды? Это может быть 10 стаканов или меньше 10 стаканов. Пока мы не измерим количество жидкости, то всё, что мы можем сказать о наполнении стакана, то это то, что оно «меньше или равно» 10 стаканам.

Для показа данного отношения с помощью символов мы добавляем внизу дополнительную строку символа больше или меньше. Например:

Знак «больше или равно»: ≥
Знак «меньше или равно»: ≤

Зачем использовать данные знаки? Дело в том, что есть вещи, полной информации о которых мы не имеем, но, тем не менее, можем о них что-то полагать. Таким образом, у нас есть различные способы сказать то, что мы знаем, хоть и не до конца (это может быть полезно).

Пример:

У Олега было 10 яблок, но он потерял несколько. Сколько у него сейчас?
Ответ: У него должно быть меньше 10 яблок.
То есть: яблоки у Олега < 10

Если у Олега все еще есть яблоки, мы также можем сказать, что у него больше нуля яблок? Конечно.
То есть: яблоки у Олега > 0

Но если бы мы думали, что Олег мог потерять все свои яблоки, мы бы сказали:
яблоки у Олега ≥ 0

Другими словами, количество яблок больше или равно нулю.

Это пригодится: решение примеров по фотографии онлайн.

Обучение с использованием символов «больше» или «меньше»

Дети знакомятся с символами «больше» и «меньше» ещё в 1 классе, в процессе обучения пониманию единиц, из которых могут быть составлены числа. Но они не всегда могут запомнить правильную позицию данного знака. В этом случае им могут помочь пару полезных способов.

Способ №1. Рот крокодила

Самый распространенный способ объяснить, как работают символы «больше чем» и «меньше чем», — это сравнить их со пастью крокодила. Нужно объяснить, что крокодил всегда хочет наесться побольше, и съесть большее число. Это простое и красочное объяснение, апеллирует к воображению детей и помогает им правильно использовать данные символы.

Крокодил всегда хочет большего

Например, если у нас есть числа 72 и 45, мы могли бы сказать, что крокодил хочет съесть число 72, так как это число с более высоким значением. Затем мы добавим символы, чтобы это выглядело так:

72 > 45 (пасть крокодила направлена в сторону большего числа).

Способ №2. Метод точек

Знаки больше или меньше можно сравнить с тремя точка. Там где меньшая сторона знака – там одна точка посередине, а где большая – две точки, одна снизу, а вторая сверху. Выглядит это примерно так:

Мы ставим две точки всегда к числу, которое больше другого. И одной точкой – к числу, которое меньше другого. Таким образом, вы всегда поставите нужный символ.

Объединение знаков

Иногда мы можем объединить два (или более) сочетания в одной строке:

Пример: Аня имеет 100 рублей, покупает что-то и говорит: «У меня есть сдача».

Сколько же она могла потратить?

Ответ: что-то больше 0 рублей и меньше 100 рублей (но НЕ 0 или 100 рублей):

«Сколько Аня тратит» > 0 рублей

«Что тратит Аня» < 100 рублей

Это можно записать всего в одну строку:

Рублей 0 < «Сколько Аня тратит» < Рублей 100.

Ключевые советы по работе с неравенствами

Выяснив, в какую сторону пишутся символы больше, меньше или равно, упомянем также работу с неравенствами. Неравенства сложны, так мы привыкли иметь четкие ответы на математические задачи, но неравенства не всегда дают нам это. Когда вы имеете с неравенством, помните о следующих правилах для облегчения процесса:

Изолируйте переменные. При работе в неравенствах с переменными, важно помнить, что вы пытаетесь изолировать переменную в ту или иную сторону. Сосредоточьтесь на сжатии чисел, если это возможно, с целью получить одну переменную в обеих сторонах вашего уравнения;
Отрицательные числа изменяют знак больше или меньше. Не забывайте, что выполнение определенных действий может переворачивать знак. Когда вы умножаете или делите на отрицательное число, будет необходимо перевернуть знак «меньше» или «больше» вместе с ним;
Избегайте умножения или деления на переменные. Если вы не уверены, что переменная всегда будет положительной или отрицательной, не умножайте и не делите неравенство на указанную переменную.

Знаки больше или меньше на клавиатуре

Знаки «больше» или «меньше» можно найти на клавиатуре внизу справа, переключившись на английскую раскладку. Достаточно зажать клавишу «Shift», и нажав на кнопку «Б» вы получите знак «меньше» (<), а нажав на кнопку «Ю» — знак «больше» (>).

Видео:

В нашем материале мы разобрали, в какую сторону направлен символ больше, меньше или равно, как не ошибиться с употреблением данных знаков, и что при этом стоит учитывать. Используйте представленный нами инструментарий, позволяющий разобраться в правильном применении данных знаков. И избежать ошибок при письменном оформлении соотношений имеющихся у вас чисел.

Источник

Существуют четыре основных арифметических действия: сложение, вычитание, умножение и деление. Они – основа математики, с их помощью производятся все остальные, более сложные вычисления. Сложение и вычитание – простейшие из них и взаимно противоположны. Но с терминами, используемыми при сложении, мы чаще сталкиваемся в жизни.

Говорим о «сложении усилий» при старании совместно получить нужный результат, о «слагаемых достигнутого успеха» и т.п. Названия же, связанные с вычитанием, остаются в пределах математики, редко появляясь в повседневной речи. Поэтому менее привычны слова вычитаемое, уменьшаемое, разность. Правило нахождения каждого из данных компонентов возможно применить лишь при понимании значения этих названий.

Значение терминов

В отличие от многих научных терминов, имеющих греческое, латинское или арабское происхождение, в данном случае используются слова с русскими корнями. Так что понять их значение несложно, а значит легко и запомнить, что каким термином обозначается.

Термины

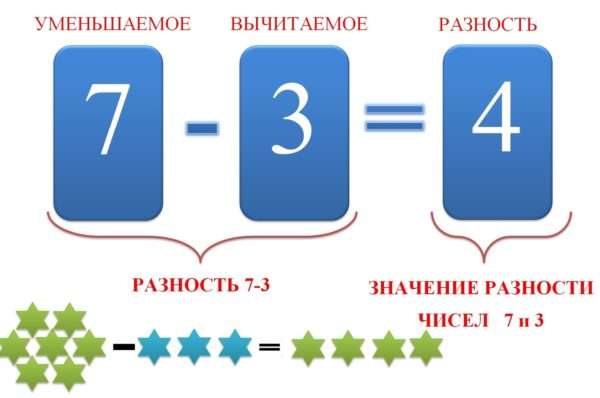
Что такое разность чисел в математике

Если присмотреться к самому названию, становится заметно, что оно имеет отношение к словам «разный», «разница». Из этого можно заключить, что имеется в виду установленная разница между количествами.

Это интересно! Как раскрыть модуль действительного числа и что это такое

Данное понятие в математике означает:

разницу между двумя числами,
это показатель того, насколько одно количество больше или меньше другого,
это результат, полученный при выполнении вычитания такое определение предлагает школьная программа.

Обратите внимание! Если количества равны друг другу, то между ними нет разницы. Значит разность их равняется нулю.

Что такое уменьшаемое и вычитаемое

Как следует из названия, уменьшаемое – это то, что делают меньше. А сделать количество меньшим можно, отняв от него часть. Таким образом, уменьшаемым называется число, от которого отнимают часть.

Вычитаемым, соответственно, называется то число, которое от него отнимают.

Уменьшаемое	Вычитаемое		Разность
18	11	=	7
14	5	=	9
26	22	=	4

Полезное видео: уменьшаемое, вычитаемое, разность

Правила нахождения неизвестного элемента

Разобравшись в терминах, несложно установить, по какому правилу находится каждый из элементов вычитания.

Поскольку разность – результат данного арифметического действия, то ее и находят с помощью этого действия, никаких других правил тут не требуется. Но они есть на случай, если неизвестен другой член математического выражения.

Это интересно! Уроки математики: умножение на ноль главное правило

Как найти уменьшаемое

Данным термином, как было выяснено, называют количество, из которого вычли часть. Но если одну вычли, а другая осталась в итоге, следовательно, из этих двух частей число и состоит. Получается, что найти неизвестное уменьшаемое можно, сложив два известных элемента.

Итак, в данном случае, чтобы найти неизвестное, следует выполнить сложение вычитаемого и разности:

–

Искомое находится путем сложения известных элементов:

Так же и во всех подобных случаях:

?	–	5	=	9
9	+	5	=	14

?	–	22	=	4
4	+	22	=	26

Как найти вычитаемое

Если целое состоит из двух частей (в данном случае количеств), то при вычитании одной из них в результате получится вторая. Таким образом, чтобы найти неизвестное вычитаемое, достаточно вместо него вычесть из целого разность.

–

Из примера видно, что от 18 отняли некоторую величину, и осталось 7. Чтобы найти эту величину, надо от 18 отнять 7.

–

По тому же правилу решаются и другие подобные примеры.

14	–	?	=	9
14	–	9	=	5

26	–	?	=	4
26	–	4	=	22

Таким образом, зная точное значение названий, можно легко догадаться, по какому правилу следует искать каждый неизвестный элемент.

Это интересно! Как разложить на множители квадратный трехчлен: формула

Полезное видео: как найти неизвестное уменьшаемое

Вывод

Четыре основных арифметических действия – та база, на которой основываются все математические вычисления, от простых до самых сложных. Конечно, в наше время, когда люди стремятся перепоручить технике все вплоть до мыслительного процесса, привычнее и быстрее производить вычисления с помощью калькулятора. Но любое умение увеличивает независимость человека – от технических средств, от окружающих. Не обязательно делать математику своей специальностью, но обладать хотя бы минимальными знаниями и умениями – значит иметь дополнительную опору для собственной уверенности.

Источник

Как пишется знак больше меньше в математике

Что значит «меньше или равно»?

Пример:

Обучение с использованием символов «больше» или «меньше»

Способ №1. Рот крокодила

Способ №2. Метод точек

Объединение знаков

Ключевые советы по работе с неравенствами

Знаки больше или меньше на клавиатуре

Видео:

Значение терминов

Что такое разность чисел в математике

Что такое уменьшаемое и вычитаемое

Полезное видео: уменьшаемое, вычитаемое, разность

Правила нахождения неизвестного элемента

Как найти уменьшаемое

<img loading="lazy" decoding="async" src="https://tvercult.ru/wp-content/uploads/2019/03/mgokpmwe.jpg" alt="Вычитаемое уменьшаемое разность правило" width="600" height="450" />

Как найти вычитаемое

Полезное видео: как найти неизвестное уменьшаемое

Вывод

Не пропустите и эти статьи: