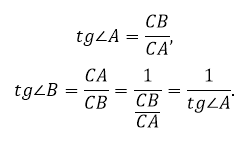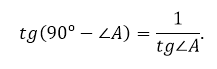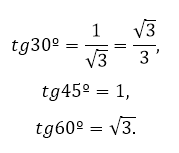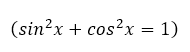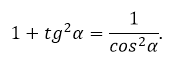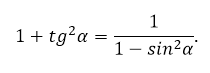- Определение
- График тангенса
- Свойства тангенса
- Обратная к тангенсу функция
- Таблица тангенсов
Определение
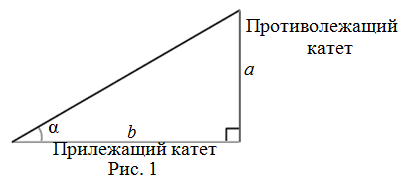
Тангенс острого угла α (tg α или tan α) – это отношение противолежащего катета (a) к прилежащему (b) в прямоугольном треугольнике.
tg α = a / b
Например:
a = 3
b = 4
tg α = a / b = 3 / 4 = 0.75
График тангенса
Функция тангенса пишется как y = tg (x). График в общем виде выглядит следующим образом:
Свойства тангенса
Ниже в табличном виде представлены основные свойства тангенса с формулами.
| Свойство | Формула |
| Симметричность | tg (-α) = -tg α |
| Симметричность | tg (90°- α) = ctg α |
| Тригонометрические тождества | tg α = sin α / cos α |
| tg α = 1 / ctg α | |
| Тангенс двойного угла | tg 2α = 2 tg α / (1 — tg2α) |
| Тангенс суммы углов | tg (α+β) = (tg α + tg β) / (1 — tg α tg β) |
| Тангенс разности углов | tg (α-β) = (tg α — tg β) / (1 + tg α tg β) |
| Сумма тангенсов | tg α + tg β = sin (α + β) / cos α cos β |
| Разность тангенсов | tg α — tg β = sin (α — β) / cos α cos β |
| Произведение тангенсов | tg α tg β = (tg α + tg β) / (ctg α + ctg β) |
 |
|
| Произведение тангенса и котангенса | tg α ctg β = (tg α + ctg β) / (ctg α + tg β) |
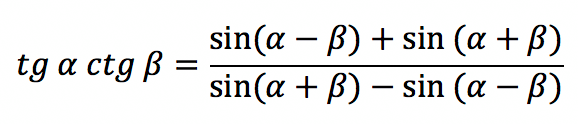 |
|
| Производная тангенса | tg’ x = 1 / cos2 (x) |
| Интеграл тангенса | ∫ tg x dx = -ln |cos x| + C |
| Формула Эйлера | tg x = (eix — e—ix) / i(eix + e—ix) |
microexcel.ru
Обратная к тангенсу функция
Арктангенс x – это обратная функция к тангенсу x, где x – любое число (x∈ℝ).
Если тангенс угла у равняется х (tg y = x), значит арктангенс x равен у:
arctg x = tg-1 x = y
Например:
arctg 1 = tg-1 1 = 45° = π/4 рад
Таблица тангенсов
| x (°) | x (рад) | tg x |
| -90° | -π/2 | -∞ |
| -71.565° | -1.2490 | -3 |
| -63.435° | -1.1071 | -2 |
| -60° | -π/3 | -√3 |
| -45° | -π/4 | -1 |
| -30° | -π/6 | -1/√3 |
| -26.565° | -0.4636 | -0.5 |
| 0° | 0 | 0 |
| 26.565° | 0.4636 | 0.5 |
| 30° | π/6 | 1/√3 |
| 45° | π/4 | 1 |
| 60° | π/3 | √3 |
| 63.435° | 1.1071 | 2 |
| 71.565° | 1.2490 | 3 |
| 90° | π/2 | ∞ |
microexcel.ru
Что такое тангенс угла и как его найти
Живущим людям на Земле
всегда хотелось знать,
как путь найти в пустыне, море,
и можно к звёздам ли попасть.
Хотелось труд свой облегчить,
создать машины, чтоб летать.
И чтоб вопросы разрешить,
пришлось про тангенс всем узнать.
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Впервые встречаясь с тригонометрией в восьмом классе на геометрии, школьники оглядываются на свою жизнь, задавая вопрос, насколько пригодится им эта область науки в дальнейшем.
Редко кто задумывается, что раздел математики, позволяющий рассказать о заданном треугольнике всё (найти все его стороны и углы, выделить особенности), позволил в своё время сделать великие открытия.
Тригонометрия, дав возможность строить корабли и самолёты, отправлять человека в космос, создавать приборы для ориентирования на море, в лесу, в пустыне, определять расстояния, не измеряя их непосредственно линейкой, шагами или чем-то иным, помогла упростить жизнь человечества, раскрыть новые горизонты знаний.
Тангенс угла
Первые встречи с тангенсом происходят при изучении прямоугольных треугольников.
В них соотношения сторон, образующих прямой угол (катетов), и стороны, лежащей напротив угла в 90º (гипотенузы), задают важные параметры для изучения углов.
Для понимания связи между объектами рассматриваются отношения различных отрезков. Задавая связь между ними, вводят понятия синуса, косинуса (это что?), тангенса, котангенса.
Важно, что это отвлечённые понятия, не связанные с какими-либо единицами измерения.
Введя функции угла, определяют их свойства. Некоторые полученные формулы могут иметь довольно громоздкий вид. Чтобы избежать затруднённого чтения, вводятся другие объекты.
Так произошло и с тангенсом. Ему посчастливилось получить два определения. Каждое характеризует заданное отношение по-своему. С одной стороны, рассматривается связь между катетами и острыми углами прямоугольного треугольника, с другой – даётся возможность упростить формулы, содержащие синусы и косинусы.
Мало кто задумывается, изучая тангенс в школе, что первоначально он был необходим, чтобы найти касательные линии к заданной кривой. Само понятие возникло от латинского слова tangens, которое означает «трогающий», «касающийся» и является причастием настоящего времени от tangere («трогать», «касаться»).
Тангенс — это отношение…
Итак, есть два определения:
-
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
Это определение удобно использовать при изучении геометрических фигур. Оно даёт возможность, минуя вычисления гипотенузы, находить углы или катеты. Выделяя прямоугольные треугольники в произвольных фигурах, задача по изучению свойств исследуемых объектов становится проще.
-
Тангенс – это отношение синуса к косинусу.
Благодаря этому определению, многие тригонометрические формулы принимают более удобный вид, становятся легче воспринимаемыми.
Приняты обозначения:
Вместо «тангенс угла альфа» пишут: tgα. На калькуляторах, в различных программах ЭВМ и ПК закрепилось другое обозначение: tan(α).
Как найти тангенс угла (формулы)
Первое свойство тангенса вытекает из его определения как отношения катетов.
Сумма двух непрямых углов прямоугольного треугольника равна 90º. Поэтому
Так как тангенс – это отношение катетов, то
Получается, что
Учитывая особенности некоторых треугольников (равностороннего, прямоугольного, равнобедренного), а также записанное свойство, была составлена таблица значений тангенса для углов 30º, 45º, 60º.
В частности,
Задача нахождения других углов по значению тангенса была решена с помощью составления более обширных таблиц. За счёт появления современных вычислительных средств необходимость применения табулированных значений уменьшилась.
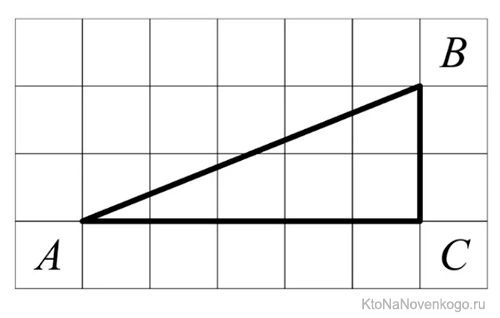
Как найти тангенс по клеточкам
Учитывая первое определение, можно определить, как найти его по клеточкам. Рисунок дополняется перпендикулярными линиями (строится высота), затем считается количество клеточек в полученном прямоугольном треугольнике на катетах, противолежащем и прилежащем искомому углу, а затем берётся их отношение.
Благодаря второму определению, задачу, как найти тангенс угла, можно решить, минуя таблицы и построение прямоугольных треугольников. Достаточно знать синус и косинус, связанные между собой основным тригонометрическим тождеством:
Из формулы тангенсов, записывающей кратко второе определение
и основного тригонометрического тождества можно понять, как найти тангенс, зная только косинус или синус угла.
Достаточно поделить основное тригонометрическое тождество на квадрат косинуса, подставить формулу тангенса. В результате получится его зависимость от косинуса:
Если выразить в последнем случае косинус, то запишется связь между тангенсом и синусом:
Тригонометрия — раздел математической науки, в котором изучаются тригонометрические функции и их использование в геометрии. Развитие тригонометрии началось еще во времена античной Греции. Во времена средневековья важный вклад в развитие этой нужной науки внесли ученые Ближнего Востока и Индии, которые придумали наиболее важные понятия, объяснили многие свойства, предложили варианты измерения и др.
Данная статья посвящена базовым понятиям и дефинициям тригонометрии. В ней рассмотрены определения основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Разъяснен и проиллюстрирован их смысл в контексте геометрии без таблиц и графиков.
Синус, косинус, тангенс и котангенс. Определения
Зачем разделять понятия синуса, косинуса, тангенса и котангенса?
Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.
Что такое синус?
Синус угла (sin α) — это отношение противолежащего этому углу катета к гипотенузе.
Что такое косинус?
Косинус угла (cosα) — это отношение прилежащего катета к гипотенузе.
Что такое тангенс?
Тангенс угла (tg α) — это отношение противолежащего катета к прилежащему.
Котангенс угла (ctg α) — отношение прилежащего катета к противолежащему.
Данные определения даны для острого угла прямоугольного треугольника!
Синус и косинус можно представить через экспоненту (экспоненциальная функция).
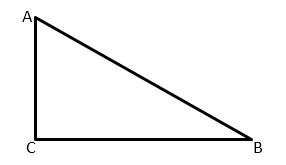
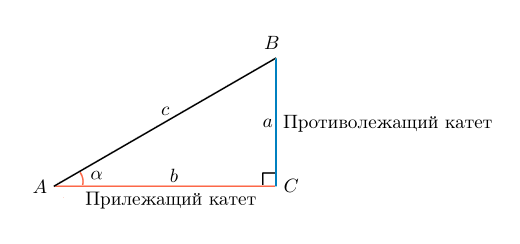
Приведем иллюстрацию.
В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.
Означения синуса, косинуса, тангенса и котангенса позволяют вычислять (находить) значения этих функций по известным длинам сторон треугольника.
Что и почему важно и принято помнить в ходе такого нахождения?
Область значений синуса и косинуса: от -1 до 1. Иными словами синус и косинус принимают значения от -1 до 1. Область значений тг и ктг — вся числовая прямая, то есть эти функции могут принимать любые значения.
Как найти синус? Для начала нужно определиться, какой перед нами треугольник: прямоугольный или произвольный. В первом случае можно использовать обычный тригонометрический метод, а во втором — теорему косинусов.
Как найти косинус? Соответственно, нам нужно знать значения прилежающего катета и гипотенузы.
Как найти тангенс? Если треугольник прямоугольный, то тангенс вычисляется при помощи значений противоположного катета и прилежащего (в уравнении нужно поделить одно на другое). Если речь идет о числах, тупых, развернутых углов и углов, превышающих 360 градусов, то тангенс определяется при помощи синуса и косинуса (посредством их отношения и деления).
Теорема синусов и косинусов используется для того чтобы искать элементы в произвольном треугольнике. Такой поиск используется часто.
Угол поворота
Определения, данные выше, относятся к острым углам. В тригонометрии вводится понятие угла поворота, величина которого, в отличие от острого угла, не ограничена рамками от 0 до 90 градусов.Угол поворота в градусах или радианах выражается любым действительным числом от -∞ до +∞.
В данном контексте можно дать определение синуса, косинуса, тангенса и котангенса угла произвольной величины. Представим единичную окружность (круг) с центром в начале декартовой системы координат.
Начальная точка A с координатами (1, 0) поворачивается вокруг центра единичной окружности на некоторый угол α и переходит в точку A1. Определение дается через координаты точки A1(x , y).
Синус угла поворота α — это ордината точки A1(x , y). sin α=y
Косинус угла поворота α — это абсцисса точки A1(x , y). cos α=икс
Тангенс угла поворота α — это отношение ординаты точки A1(x , y) к ее абсциссе. tg α=yx
Котанг угла поворота α — это отношение абсциссы точки A1(x , y) к ее ординате. ctg α=xy
Синус и косинус определены для любого угла поворота. Это логично, ведь абсциссу и ординату точки после поворота можно определить при любом угле. Иначе обстоит дело с тангенсом и котангенсом. Тангенс не определен, когда точка после поворота переходит в точку с нулевой абсциссой (0, 1) и (0, -1). В таких случаях выражение для тангенса tg α=yx просто не имеет смысла, так как в нем присутствует деление на ноль. Аналогична ситуация с котангенсом. Отличие состоит в том, что котангенс не определен в тех случаях, когда в ноль обращается ордината точки.
Простое правило: синус и косинус определены для любых углов α.
Тангенс определен для всех углов, кроме α=90°+180°·k, k∈Z (α=π2+π·k, k∈Z)
Котангенс определен для всех углов, кроме α=180°·k, k∈Z (α=π·k, k∈Z)
При решении практических примеров не говорят «синус угла поворота α». Слова «угол поворота» просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь.
Числа
Как быть с определением синуса, косинуса, тангенса и котангенса числа, а не угла поворота?
Синусом, косинусом, тангенсом и котангенсом числа t называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в t радиан.
Например, синус числа 10π равен синусу угла поворота величиной 10π рад.
Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Рассмотрим его подробнее.
Любому действительному числу t ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат. Синус, косинус, тангенс и котангенс определяются через координаты этой точки.
Начальная точка на окружности — точка A c координатами (1, 0).
Положительному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t.
Отрицательному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t.
Теперь, когда связь числа и точки на окружности установлена, переходим к определению синуса, косинуса, тангенса и котангенса.
Синус числа t — ордината точки единичной окружности, соответствующей числу t. sin t=y
Косинус числа t — абсцисса точки единичной окружности, соответствующей числу t. cos t=x
Тангенс числа t — отношение ординаты к абсциссе точки единичной окружности, соответствующей числу t. tg t=yx=sin tcos t
Последние определения находятся в соответствии и не противоречат определению, данному в начале это пункта. Точка на окружности, соответствующая числу t, совпадает с точкой, в которую переходит начальная точка после поворота на угол t радиан.
Тригонометрические функции углового и числового аргумента
Каждому значению угла α соответствует определенное значение синуса и косинуса этого угла. Также, как всем углам α, отличным от α = 90 ° + 180 ° · k , k ∈ Z ( α = π 2 + π · k , k ∈ Z ) соответствует определенное значение тангенса. Котангенс, как сказано выше, определен для всех α, кроме α = 180 ° · k , k ∈ Z ( α = π · k , k ∈ Z ).
Можно сказать, что sin α, cos α, tg α, ctg α — это функции угла альфа, или функции углового аргумента.
Аналогично можно говорить о синусе, косинусе, тангенсе и котангенсе, как о функциях числового аргумента. Каждому действительному числу t соответствует определенное значение синуса или косинуса числа t. Всем числам, отличным от π 2 + π · k , k ∈ Z соответствует значение тангенса. Котангенс, аналогично, определен для всех чисел, кроме π · k , k ∈ Z.
Синус, косинус, тангенс и котангенс — основные тригонометрические функции.
Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело.
Связь определений sin, cos, tg и ctg из геометрии и тригонометрии
Вернемся к данным в самом начале определениям и углу альфа, лежащему в пределах от 0 до 90 градусов. Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью соотношений сторон прямоугольного треугольника. Покажем это.
Возьмем единичную окружность с центром в прямоугольной декартовой системе координат. Повернем начальную точку A(1,0) на угол величиной до 90 градусов и проведем из полученной точки A1(x,y) перпендикуляр к оси абсцисс. В полученном прямоугольном треугольнике угол A1OH равен углу поворота α, длина катета OH равна абсциссе точки A1(x,y). Длина катета, противолежащего углу, равна ординате точки A1(x,y), а длина гипотенузы равна единице, так как она является радиусом единичной окружности.
В соответствии с определением из геометрии, синус угла α равен отношению противолежащего катета к гипотенузе.
sin α=A1HOA1=y1=y
Значит, определение синуса острого угла в прямоугольном треугольнике через соотношение сторон эквивалентно определению синуса угла поворота α, при альфа лежащем в пределах от 0 до 90 градусов.
Аналогично соответствие определений можно показать для косинуса, тангенса и котангенса.
Синус, косинус, тангенс и котангенс: основные формулы
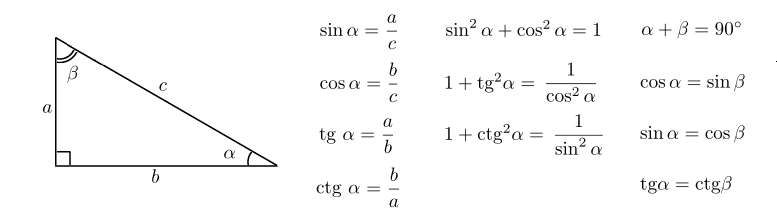
Катетами прямоугольного треугольника называются те его стороны, которые образуют прямой угол. Каждый из катетов всегда меньше гипотенузы по значению, но в сумме они обязательно ее превосходят. Зная оба катета, можно найти не только третью сторону прямоугольного треугольника – гипотенузу, по теореме Пифагора, но и углы, находящиеся между катетами и гипотенузой. Для этого используется тригонометрическое отношение тангенса угла α, которое по определению равно отношению катета, противолежащего углу α, к катету прилежащему.
Делением катета, находящегося напротив угла, на катет, который является одной из сторон угла, получается значение тангенса, соответствующее определенной градусной мере. Краткая таблица основных значений тангенса находится внизу страницы, а полная таблица всех тангенсов расположена по ссылке.
Свойства
Тангенс угла tg(α) — есть отношение противолежащего катета a к прилежащему катету b.
Таблица тангенсов
| Тангенс угла 0° градусов | 0 | 0.000 |
| Тангенс угла 30° градусов | 1/√3 | 0.577 |
| Тангенс угла 45° градусов | 1 | 1.000 |
| Тангенс угла 60° градусов | √3 | 1.732 |
| Тангенс угла 90° градусов | ∞ | ∞ |
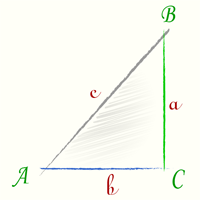 |
Тангенс угла tg(A) — есть отношение [ tg(A) = frac{a}{b} ] |
Тангенс угла — tg(A), таблица
| 0° Тангенс угла 0 градусов |
$ tg(0°) = tg(0) = 0 $ |
0.000 |
| 30° Тангенс угла 30 градусов |
$ tg(30°) = tgBig(Largefrac{pi}{6}normalsizeBig) = Largefrac{1}{sqrt{3}}normalsize $ |
0.577 |
| 45° Тангенс угла 45 градусов |
$ tg(45°) = tgBig(Largefrac{pi}{4}normalsizeBig) = 1 $ |
1.000 |
| 60° Тангенс угла 60 градусов |
$ tg(60°) = tgBig(Largefrac{pi}{3}normalsizeBig) = sqrt{3} $ |
1.732 |
| 90° Тангенс угла 90 градусов |
$ tg(90°) = tgBig(Largefrac{pi}{2}normalsizeBig) = infin $ |
∞ |
Вычислить, найти тангенс угла tg(A) и угол, в прямоугольном треугольнике
Вычислить, найти тангенс угла tg(A) по углу A в градусах
Вычислить, найти тангенс угла tg(A) по углу A в радианах
Тангенс угла — tg(A) |
стр. 224 |
|---|
Определение
Тангенс острого угла α (tg α или tan α) – это отношение противолежащего катета (a) к прилежащему (b) в прямоугольном треугольнике.
tg α = a / b
Например:
a = 3
b = 4
tg α = a / b = 3 / 4 = 0.75
График тангенса
Функция тангенса пишется как y = tg (x). График в общем виде выглядит следующим образом:
Свойства тангенса
Ниже в табличном виде представлены основные свойства тангенса с формулами.
Обратная к тангенсу функция
Арктангенс x – это обратная функция к тангенсу x, где x – любое число (x∈ℝ).
Если тангенс угла у равняется х (tg y = x), значит арктангенс x равен у:
arctg x = tg-1 x = y
Например:
arctg 1 = tg-1 1 = 45° = π/4 рад
Таблица тангенсов
| x (°) | x (рад) | tg x |
| -90° | -π/2 | -∞ |
| -71.565° | -1.2490 | -3 |
| -63.435° | -1.1071 | -2 |
| -60° | -π/3 | -√3 |
| -45° | -π/4 | -1 |
| -30° | -π/6 | -1/√3 |
| -26.565° | -0.4636 | -0.5 |
| 0° | 0 | 0 |
| 26.565° | 0.4636 | 0.5 |
| 30° | π/6 | 1/√3 |
| 45° | π/4 | 1 |
| 60° | π/3 | √3 |
| 63.435° | 1.1071 | 2 |
| 71.565° | 1.2490 | 3 |
| 90° | π/2 | ∞ |
microexcel.ru
Угол
Современные определения тригонометрических функций и их символика принадлежат Л. Эйлеру. Хотя еще в 3-м в. до н. э в трудах Архимеда, Евклида и других рассматриваются отношения сторон в прямоугольном треугольнике, что фактически и является тригонометрическими функциями. В переводе с греческого тригонометрия означает «треугольник» и «измеряю» и является разделом математики, изучающим связь между сторонами и углами треугольника. Как нам известно, в прямоугольном треугольнике 2 угла острых, а один является прямым. Стороны треугольника, прилежащие к углу, равному 90 градусов, называются катетами, с сторона напротив прямого угла является гипотенузой. Тангенс представляет собой одну из тригонометрических функций угла. Функцию тангенс для острых углов можно рассматривать как отношение двух катетов: противолежащего к прилежащему.
tg (a)=а/в
где а — катет, противолежащий углу а;
в — прилежащий катет.
Тангенс заданного угла можно определить, воспользовавшись таблицей Брадиса, где помещены тригонометрические функции всех углов. Если в задаче известна величина угла и одна из сторон треугольника, будет несложно определить остальные его стороны и углы. С помощью онлайн калькулятора ваши расчеты будут более быстрыми и правильными.
Рассчитать тангенс угла
tg (°) =
Таблица тангенсов углов от 0° до 180°
|
|
|
Таблица тангенсов углов от 180° до 360°
|
|
td width=»80″>tg (301°)
|
Содержание:
- Тангенс угла в треугольнике
- Тангенс произвольного угла
Тангенс угла в треугольнике
Определение
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего
этому углу катета к прилежащему катету (рис. 1):
$$operatorname{tg} alpha=frac{a}{b}$$
Замечание
Сравнивая определения для тангенса и
котангенса угла, можно заметить, что тангенс и котангенс угла связаны между собой соотношением:
$$
operatorname{tg} alpha=frac{1}{operatorname{ctg} alpha}
$$
Пример
Задание. Найти тангенс острого угла прямоугольного треугольника, если известно, что
прилежащий к этому углу катет равен 3 см, а противолежащий ему — на 2 сантиметра длиннее.
Решение. Вначале найдем длину противолежащего катета:
$a = 3 + 2 = 5$ (см)
Тогда тангенс угла
$$
operatorname{tg} alpha=frac{5}{3}
$$
Ответ.
$$
operatorname{tg} alpha=frac{5}{3}
$$
Тангенс произвольного угла
Определение
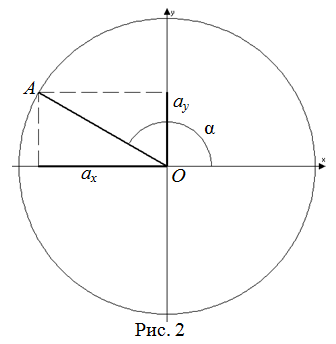
Тангенс произвольного угла
$alpha$, образованного осью
$O_x$ и произвольным радиус-вектором $overrightarrow{O A}=left(a_{x} ; a_{y}right)$ (рис. 2), — отношение
проекции этого вектора на ось
$O_y$ к его проекции на ось
$O_x$:
$$operatorname{tg} alpha=frac{a_{y}}{a_{x}}$$
Пример
Задание. Найти тангенс угла, образованного вектором
$bar{a}=(1 ;-1)$ и осью абсцисс.
Решение. Проекция на ось абсцисс равна
$a_x=1$, а на ось ординат — $a_y=-1$, тогда
$$operatorname{tg} alpha=frac{-1}{1}=-1$$
Ответ. $operatorname{tg} alpha=-1$
Читать дальше: что такое котангенс угла.

|
Тангенс угла tg(A) — есть отношение [ tg(A) = frac{a}{b} ] |
Тангенс угла — tg(A), таблица
|
0° Тангенс угла 0 градусов |
$ tg(0°) = tg(0) = 0 $ |
0.000 |
|
30° Тангенс угла 30 градусов |
$ tg(30°) = tgBig(Largefrac{pi}{6}normalsizeBig) = Largefrac{1}{sqrt{3}}normalsize $ |
0.577 |
|
45° Тангенс угла 45 градусов |
$ tg(45°) = tgBig(Largefrac{pi}{4}normalsizeBig) = 1 $ |
1.000 |
|
60° Тангенс угла 60 градусов |
$ tg(60°) = tgBig(Largefrac{pi}{3}normalsizeBig) = sqrt{3} $ |
1.732 |
|
90° Тангенс угла 90 градусов |
$ tg(90°) = tgBig(Largefrac{pi}{2}normalsizeBig) = infin $ |
∞ |
Вычислить, найти тангенс угла tg(A) и угол, в прямоугольном треугольнике
Вычислить, найти тангенс угла tg(A) по углу A в градусах
Вычислить, найти тангенс угла tg(A) по углу A в радианах
Тангенс угла — tg(A) |
стр. 224 |
|---|
Тангенс угла. Таблица тангенсов.
Тангенс угла через градусы, минуты и секунды
Тангенс угла через десятичную запись угла
Определение тангенса
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
tg(α) = sin(α)/cos(α)
tg(α) = 1/ctg(α)
Таблица тангенсов в радианах
tg(0°) = 0tg(π/12) = tg(15°) = 0.2679491924tg(π/6) = tg(30°) = 0.5773502692tg(π/4) = tg(45°) = 1tg(π/3) = tg(60°) = 1.732050808tg(5π/12) = tg(75°) = 3.732050808tg(π/2) = tg(90°) = ∞tg(7π/12) = tg(105°) = -3.732050808tg(2π/3) = tg(120°) = -1.732050808tg(3π/4) = tg(135°) = -1tg(5π/6) = tg(150°) = -0.5773502692tg(11π/12) = tg(165°) = -0.2679491924tg(π) = tg(180°) = 0tg(13π/12) = tg(195°) = 0.2679491924tg(7π/6) = tg(210°) = 0.5773502692tg(5π/4) = tg(225°) = 1tg(4π/3) = tg(240°) = 1.732050808tg(17π/12) = tg(255°) = 3.732050808tg(3π/2) = tg(270°) = ∞tg(19π/12) = tg(285°) = -3.732050808tg(5π/3) = tg(300°) = -1.732050808tg(7π/4) = tg(315°) = -1tg(11π/6) = tg(330°) = -0.5773502692tg(23π/12) = tg(345°) = -0.2679491924
Таблица Брадиса тангенсы
| tg(0) = 0 | tg(120) = -1.732050808 | tg(240) = 1.732050808 |
| tg(1) = 0.01745506493 | tg(121) = -1.664279482 | tg(241) = 1.804047755 |
| tg(2) = 0.03492076949 | tg(122) = -1.600334529 | tg(242) = 1.880726465 |
| tg(3) = 0.05240777928 | tg(123) = -1.539864964 | tg(243) = 1.962610506 |
| tg(4) = 0.06992681194 | tg(124) = -1.482560969 | tg(244) = 2.050303842 |
| tg(5) = 0.08748866353 | tg(125) = -1.428148007 | tg(245) = 2.144506921 |
| tg(6) = 0.1051042353 | tg(126) = -1.37638192 | tg(246) = 2.246036774 |
| tg(7) = 0.1227845609 | tg(127) = -1.327044822 | tg(247) = 2.355852366 |
| tg(8) = 0.1405408347 | tg(128) = -1.279941632 | tg(248) = 2.475086853 |
| tg(9) = 0.1583844403 | tg(129) = -1.234897157 | tg(249) = 2.605089065 |
| tg(10) = 0.1763269807 | tg(130) = -1.191753593 | tg(250) = 2.747477419 |
| tg(11) = 0.1943803091 | tg(131) = -1.150368407 | tg(251) = 2.904210878 |
| tg(12) = 0.2125565617 | tg(132) = -1.110612515 | tg(252) = 3.077683537 |
| tg(13) = 0.2308681911 | tg(133) = -1.07236871 | tg(253) = 3.270852618 |
| tg(14) = 0.2493280028 | tg(134) = -1.035530314 | tg(254) = 3.487414444 |
| tg(15) = 0.2679491924 | tg(135) = -1 | tg(255) = 3.732050808 |
| tg(16) = 0.2867453858 | tg(136) = -0.9656887748 | tg(256) = 4.010780934 |
| tg(17) = 0.3057306815 | tg(137) = -0.9325150861 | tg(257) = 4.331475874 |
| tg(18) = 0.3249196962 | tg(138) = -0.9004040443 | tg(258) = 4.704630109 |
| tg(19) = 0.3443276133 | tg(139) = -0.8692867378 | tg(259) = 5.144554016 |
| tg(20) = 0.3639702343 | tg(140) = -0.8390996312 | tg(260) = 5.67128182 |
| tg(21) = 0.383864035 | tg(141) = -0.8097840332 | tg(261) = 6.313751515 |
| tg(22) = 0.4040262258 | tg(142) = -0.7812856265 | tg(262) = 7.115369722 |
| tg(23) = 0.4244748162 | tg(143) = -0.7535540501 | tg(263) = 8.144346428 |
| tg(24) = 0.4452286853 | tg(144) = -0.726542528 | tg(264) = 9.514364454 |
| tg(25) = 0.4663076582 | tg(145) = -0.7002075382 | tg(265) = 11.4300523 |
| tg(26) = 0.4877325886 | tg(146) = -0.6745085168 | tg(266) = 14.30066626 |
| tg(27) = 0.5095254495 | tg(147) = -0.6494075932 | tg(267) = 19.08113669 |
| tg(28) = 0.5317094317 | tg(148) = -0.6248693519 | tg(268) = 28.63625328 |
| tg(29) = 0.5543090515 | tg(149) = -0.600860619 | tg(269) = 57.28996163 |
| tg(30) = 0.5773502692 | tg(150) = -0.5773502692 | tg(270) = ∞ |
| tg(31) = 0.600860619 | tg(151) = -0.5543090515 | tg(271) = -57.28996163 |
| tg(32) = 0.6248693519 | tg(152) = -0.5317094317 | tg(272) = -28.63625328 |
| tg(33) = 0.6494075932 | tg(153) = -0.5095254495 | tg(273) = -19.08113669 |
| tg(34) = 0.6745085168 | tg(154) = -0.4877325886 | tg(274) = -14.30066626 |
| tg(35) = 0.7002075382 | tg(155) = -0.4663076582 | tg(275) = -11.4300523 |
| tg(36) = 0.726542528 | tg(156) = -0.4452286853 | tg(276) = -9.514364454 |
| tg(37) = 0.7535540501 | tg(157) = -0.4244748162 | tg(277) = -8.144346428 |
| tg(38) = 0.7812856265 | tg(158) = -0.4040262258 | tg(278) = -7.115369722 |
| tg(39) = 0.8097840332 | tg(159) = -0.383864035 | tg(279) = -6.313751515 |
| tg(40) = 0.8390996312 | tg(160) = -0.3639702343 | tg(280) = -5.67128182 |
| tg(41) = 0.8692867378 | tg(161) = -0.3443276133 | tg(281) = -5.144554016 |
| tg(42) = 0.9004040443 | tg(162) = -0.3249196962 | tg(282) = -4.704630109 |
| tg(43) = 0.9325150861 | tg(163) = -0.3057306815 | tg(283) = -4.331475874 |
| tg(44) = 0.9656887748 | tg(164) = -0.2867453858 | tg(284) = -4.010780934 |
| tg(45) = 1 | tg(165) = -0.2679491924 | tg(285) = -3.732050808 |
| tg(46) = 1.035530314 | tg(166) = -0.2493280028 | tg(286) = -3.487414444 |
| tg(47) = 1.07236871 | tg(167) = -0.2308681911 | tg(287) = -3.270852618 |
| tg(48) = 1.110612515 | tg(168) = -0.2125565617 | tg(288) = -3.077683537 |
| tg(49) = 1.150368407 | tg(169) = -0.1943803091 | tg(289) = -2.904210878 |
| tg(50) = 1.191753593 | tg(170) = -0.1763269807 | tg(290) = -2.747477419 |
| tg(51) = 1.234897157 | tg(171) = -0.1583844403 | tg(291) = -2.605089065 |
| tg(52) = 1.279941632 | tg(172) = -0.1405408347 | tg(292) = -2.475086853 |
| tg(53) = 1.327044822 | tg(173) = -0.1227845609 | tg(293) = -2.355852366 |
| tg(54) = 1.37638192 | tg(174) = -0.1051042353 | tg(294) = -2.246036774 |
| tg(55) = 1.428148007 | tg(175) = -0.08748866353 | tg(295) = -2.144506921 |
| tg(56) = 1.482560969 | tg(176) = -0.06992681194 | tg(296) = -2.050303842 |
| tg(57) = 1.539864964 | tg(177) = -0.05240777928 | tg(297) = -1.962610506 |
| tg(58) = 1.600334529 | tg(178) = -0.03492076949 | tg(298) = -1.880726465 |
| tg(59) = 1.664279482 | tg(179) = -0.01745506493 | tg(299) = -1.804047755 |
| tg(60) = 1.732050808 | tg(180) = 0 | tg(300) = -1.732050808 |
| tg(61) = 1.804047755 | tg(181) = 0.01745506493 | tg(301) = -1.664279482 |
| tg(62) = 1.880726465 | tg(182) = 0.03492076949 | tg(302) = -1.600334529 |
| tg(63) = 1.962610506 | tg(183) = 0.05240777928 | tg(303) = -1.539864964 |
| tg(64) = 2.050303842 | tg(184) = 0.06992681194 | tg(304) = -1.482560969 |
| tg(65) = 2.144506921 | tg(185) = 0.08748866353 | tg(305) = -1.428148007 |
| tg(66) = 2.246036774 | tg(186) = 0.1051042353 | tg(306) = -1.37638192 |
| tg(67) = 2.355852366 | tg(187) = 0.1227845609 | tg(307) = -1.327044822 |
| tg(68) = 2.475086853 | tg(188) = 0.1405408347 | tg(308) = -1.279941632 |
| tg(69) = 2.605089065 | tg(189) = 0.1583844403 | tg(309) = -1.234897157 |
| tg(70) = 2.747477419 | tg(190) = 0.1763269807 | tg(310) = -1.191753593 |
| tg(71) = 2.904210878 | tg(191) = 0.1943803091 | tg(311) = -1.150368407 |
| tg(72) = 3.077683537 | tg(192) = 0.2125565617 | tg(312) = -1.110612515 |
| tg(73) = 3.270852618 | tg(193) = 0.2308681911 | tg(313) = -1.07236871 |
| tg(74) = 3.487414444 | tg(194) = 0.2493280028 | tg(314) = -1.035530314 |
| tg(75) = 3.732050808 | tg(195) = 0.2679491924 | tg(315) = -1 |
| tg(76) = 4.010780934 | tg(196) = 0.2867453858 | tg(316) = -0.9656887748 |
| tg(77) = 4.331475874 | tg(197) = 0.3057306815 | tg(317) = -0.9325150861 |
| tg(78) = 4.704630109 | tg(198) = 0.3249196962 | tg(318) = -0.9004040443 |
| tg(79) = 5.144554016 | tg(199) = 0.3443276133 | tg(319) = -0.8692867378 |
| tg(80) = 5.67128182 | tg(200) = 0.3639702343 | tg(320) = -0.8390996312 |
| tg(81) = 6.313751515 | tg(201) = 0.383864035 | tg(321) = -0.8097840332 |
| tg(82) = 7.115369722 | tg(202) = 0.4040262258 | tg(322) = -0.7812856265 |
| tg(83) = 8.144346428 | tg(203) = 0.4244748162 | tg(323) = -0.7535540501 |
| tg(84) = 9.514364454 | tg(204) = 0.4452286853 | tg(324) = -0.726542528 |
| tg(85) = 11.4300523 | tg(205) = 0.4663076582 | tg(325) = -0.7002075382 |
| tg(86) = 14.30066626 | tg(206) = 0.4877325886 | tg(326) = -0.6745085168 |
| tg(87) = 19.08113669 | tg(207) = 0.5095254495 | tg(327) = -0.6494075932 |
| tg(88) = 28.63625328 | tg(208) = 0.5317094317 | tg(328) = -0.6248693519 |
| tg(89) = 57.28996163 | tg(209) = 0.5543090515 | tg(329) = -0.600860619 |
| tg(90) = ∞ | tg(210) = 0.5773502692 | tg(330) = -0.5773502692 |
| tg(91) = -57.28996163 | tg(211) = 0.600860619 | tg(331) = -0.5543090515 |
| tg(92) = -28.63625328 | tg(212) = 0.6248693519 | tg(332) = -0.5317094317 |
| tg(93) = -19.08113669 | tg(213) = 0.6494075932 | tg(333) = -0.5095254495 |
| tg(94) = -14.30066626 | tg(214) = 0.6745085168 | tg(334) = -0.4877325886 |
| tg(95) = -11.4300523 | tg(215) = 0.7002075382 | tg(335) = -0.4663076582 |
| tg(96) = -9.514364454 | tg(216) = 0.726542528 | tg(336) = -0.4452286853 |
| tg(97) = -8.144346428 | tg(217) = 0.7535540501 | tg(337) = -0.4244748162 |
| tg(98) = -7.115369722 | tg(218) = 0.7812856265 | tg(338) = -0.4040262258 |
| tg(99) = -6.313751515 | tg(219) = 0.8097840332 | tg(339) = -0.383864035 |
| tg(100) = -5.67128182 | tg(220) = 0.8390996312 | tg(340) = -0.3639702343 |
| tg(101) = -5.144554016 | tg(221) = 0.8692867378 | tg(341) = -0.3443276133 |
| tg(102) = -4.704630109 | tg(222) = 0.9004040443 | tg(342) = -0.3249196962 |
| tg(103) = -4.331475874 | tg(223) = 0.9325150861 | tg(343) = -0.3057306815 |
| tg(104) = -4.010780934 | tg(224) = 0.9656887748 | tg(344) = -0.2867453858 |
| tg(105) = -3.732050808 | tg(225) = 1 | tg(345) = -0.2679491924 |
| tg(106) = -3.487414444 | tg(226) = 1.035530314 | tg(346) = -0.2493280028 |
| tg(107) = -3.270852618 | tg(227) = 1.07236871 | tg(347) = -0.2308681911 |
| tg(108) = -3.077683537 | tg(228) = 1.110612515 | tg(348) = -0.2125565617 |
| tg(109) = -2.904210878 | tg(229) = 1.150368407 | tg(349) = -0.1943803091 |
| tg(110) = -2.747477419 | tg(230) = 1.191753593 | tg(350) = -0.1763269807 |
| tg(111) = -2.605089065 | tg(231) = 1.234897157 | tg(351) = -0.1583844403 |
| tg(112) = -2.475086853 | tg(232) = 1.279941632 | tg(352) = -0.1405408347 |
| tg(113) = -2.355852366 | tg(233) = 1.327044822 | tg(353) = -0.1227845609 |
| tg(114) = -2.246036774 | tg(234) = 1.37638192 | tg(354) = -0.1051042353 |
| tg(115) = -2.144506921 | tg(235) = 1.428148007 | tg(355) = -0.08748866353 |
| tg(116) = -2.050303842 | tg(236) = 1.482560969 | tg(356) = -0.06992681194 |
| tg(117) = -1.962610506 | tg(237) = 1.539864964 | tg(357) = -0.05240777928 |
| tg(118) = -1.880726465 | tg(238) = 1.600334529 | tg(358) = -0.03492076949 |
| tg(119) = -1.804047755 | tg(239) = 1.664279482 | tg(359) = -0.01745506493 |
Похожие калькуляторы
Тангенсом угла в прямоугольном треугольнике называют отношение противолежащего катета к прилежащему.
Катетами являются стороны, которые образуют прямой угол в треугольнике, соответственно, гипотенузой является третья (самая длинная) сторона.
Для простоты запоминания можно дать такое определение: тангенс угла — это отношение дальнего от рассматриваемого угла катета к ближнему катету.
В случае с рисунком, описанным выше: tgα=abtgalpha=frac{a}{b}
Тангенс можно найти напрямую пользуясь данной формулой, а можно и через тригонометрические тождества. Разберем подробнее задачи.
В прямоугольном треугольнике катеты равны 6 см6text{ см} и 8 см8text{ см}. Найдите тангенс угла, близлежащего к меньшей стороне.
Решение
a=8a=8
b=6b=6
tgα=ab=86≈1.33tgalpha=frac{a}{b}=frac{8}{6}approx1.33
Ответ
1.331.33
Формулу:
tgα=abtgalpha=frac{a}{b}
Можно записать в следующем виде:
tgα=sinαcosαtgalpha=frac{sinalpha}{cosalpha}
Проверим истинность данного выражения. Подставим вместо синуса и косинуса их определения:
tgα=sinαcosα=acbc=abtgalpha=frac{sinalpha}{cosalpha}=frac{frac{a}{c}}{frac{b}{c}}=frac{a}{b}
Получили первичное равенство, значит выражение для тангенса через отношение синуса к косинусу верно.
Решим задачу, пользуясь этой формулой.
По условию задачи известен косинус угла, равный 32frac{sqrt{3}}{2} и синус того же угла, равный 12frac{1}{2}. Найдите тангенс данного угла.
Решение
cosα=32cosalpha=frac{sqrt{3}}{2}
sinα=12sinalpha=frac{1}{2}
tgα=sinαcosα=1232=13tgalpha=frac{sinalpha}{cosalpha}=frac{frac{1}{2}}{frac{sqrt{3}}{2}}=frac{1}{sqrt{3}}
Ответ
13frac{1}{sqrt{3}}
Еще одно тождество помогает решить задачи, связанные с тангенсом:
1+tg2α=1cos2α1+tg^2alpha=frac{1}{cos^2alpha}
Оно появляется путем деление каждого слагаемого основного тождества тригонометрии на квадрат косинуса.
Известен квадрат косинуса угла в прямоугольном треугольнике, равный 0.80.8. Нужно найти тангенс этого угла.
Решение
cos2α=0.8cos^2alpha=0.8
1+tg2α=1cos2α1+tg^2alpha=frac{1}{cos^2alpha}
1+tg2α=10.81+tg^2alpha=frac{1}{0.8}
1+tg2α=1.251+tg^2alpha=1.25
tg2α=0.25tg^2alpha=0.25
tgα=0.25tgalpha=sqrt{0.25}
tgα=0.5tgalpha=0.5
Ответ
0.50.5
У вас есть трудности с вычислением тангенса? Можете заказать задачу по математике у наших экспертов!