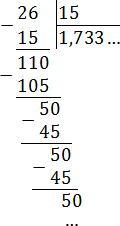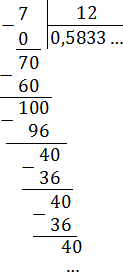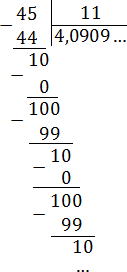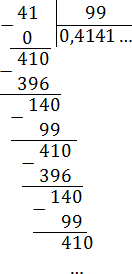Как записать число в периоде
Простые арифметические операции, такие как вычитание, сложение, умножение и деление, не всегда дают простой результат. Например, при осуществлении деления может выясниться, что частное представляет собой число в периоде, которое необходимо правильно записать.

Операция деления предполагает участие в ней нескольких основных компонентов. Первый из них — так называемое делимое, то есть число, которое подвергается процедуре деления. Второй — делитель, то есть число, на которое производится деление. Третий — частное, то есть результат операции деления делимого на делитель.
Самым простым вариантом результата, который может получиться при использовании в качестве делимого и делителя двух целых положительных чисел, является еще одно целое положительное число. Например, при делении 6 на 2 частное будет равно 3. Такая ситуация возможна, если делимое является кратным делителю, то есть без остатка делится на него.
Однако существуют и другие варианты, когда осуществить операцию деления без остатка невозможно. В этом случае частным становится нецелое число, которое можно записать в виде комбинации целой и дробной частей. Например, при делении 5 на 2 частное составит 2,5.
Один из вариантов, который может получиться в случае, если делимое не является кратным делителю, представляет собой так называемое число в периоде. Оно может возникнуть в результате деления в том случае, если частное оказывается бесконечно повторяющимся набором цифр. Например, число в периоде может появиться при делении числа 2 на 3. В этой ситуации результат, выраженный в виде десятичной дроби, будет выражен в виде комбинации бесконечного количества цифр 6 после запятой.
Для того чтобы обозначить результат такого деления, был изобретен специальный способ записи чисел в периоде: такое число обозначается помещением повторяющейся цифры в скобки. Например, результат деления 2 на 3 будет записываться с использованием этого способа как 0,(6). Указанный вариант записи применим также в случае, если повторяющейся является только часть числа, получившегося в результате деления.
Например, при делении 5 на 6 результатом будет периодическое число, имеющее вид 0,8(3). Использование этого способа, во-первых, является наиболее эффективным по сравнению с попыткой записать все или часть цифр числа в периоде, во-вторых, обладает большей точностью в сравнении с другим способом передачи таких чисел — округлением, а кроме того, позволяет отличить числа в периоде от точной десятичной дроби с соответствующим значением при сопоставлении величины этих чисел. Так, например, очевидно, что 0,(6) — существенно больше, чем 0,6.
Видео по теме
Морфемный разбор слова:
Однокоренные слова к слову:
ПЕРИОД
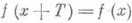
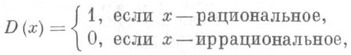
любое рациональное число 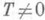
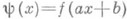
Аналогично определяется П. функции, определенной на нек-рой абелевой группе. А. А. Конюшков.
Полезное
Смотреть что такое «ПЕРИОД» в других словарях:
Период — (греч. periodos «обход», «окружность») термин, введенный Аристотелем для обозначения «речи, имеющей в себе самой начало и конец и легко обнимаемой умом». Под П. следует понимать так. обр. большую синтаксическую единицу, сложное предложение или… … Литературная энциклопедия
ПЕРИОД — периода, м. [греч. periodos] (книжн.). 1. Промежуток времени, в течение к–рого заканчивается какой–н. повторяющийся процесс (науч.). Синодический период обращения планеты (время, в течение к–рого планета совершает один полный оборот вокруг… … Толковый словарь Ушакова
Период — ПЕРИОД (Περιοδος обход, окружность). Этим словом в древней Греции называлась та замкнутая, кольцевая дорога, на которой происходили игры и состязания во время олимпийских празднеств. Этим термином Аристотель стал обозначать особый вид… … Словарь литературных терминов
ПЕРИОД — (греч. periodos путь кругом). 1) промежуток времени между двумя важными историческими событиями. 2) в астрономии то же, что цикл; в арифметике: число цифр, повторяющихся, в том же порядке, бесчисленное множество раз. 3) особенно развитое сложное… … Словарь иностранных слов русского языка
период — а, м. période f. <лат. periodus<гр. periodos обход, круговращение, орбита небесного тела. 1. Промежуток времени, в который протекает та или иная часть общего процесса. БАС 1. Бывают в жизни его периоды во время которых выступает он из… … Исторический словарь галлицизмов русского языка
ПЕРИОД — муж. срок или промежуток времени, продолжительность; время от одного события до другого. История делится на периоды, сроки. Период первозданный период осадочный, сроки образованья земной толщи. | Длительность самого события, действия, состоянья;… … Толковый словарь Даля
ПЕРИОД — (1) промежуток времени, в течение которого начинается, развивается и заканчивается какой либо процесс; наименьший интервал времени, по истечении которого произвольно выбранные мгновенные значения периодической величины повторяются; (2) П. в… … Большая политехническая энциклопедия
Период С — Студийный а … Википедия
ПЕРИОД — срок протекания экономического процесса, действия, плана, договора, гарантии, уплаты долгов, внесения налогов, выполнения работ (гарантийный период, плановый период, период обложения, период окупаемости). Райзберг Б.А., Лозовский Л.Ш.,… … Экономический словарь
период — См … Словарь синонимов
ПЕРИОД — колебаний, наименьший промежуток времени, через который совершающая колебания система возвращается в то же состояние, в котором она находилась в начальный момент, выбранный произвольно. Период величина, обратная частоте колебаний. Понятие период… … Современная энциклопедия
Источник
Периодические дроби
Существуют дроби, у которых в дробной части некоторые цифры бесконечно повторяются. Выглядят эти дроби следующим образом:
Дроби такого вида называют периодическими. В данном уроке мы попробуем разобраться, что это за дроби и как с ними работать.
Получаем периодическую дробь
Попробуем разделить 1 на 3. Не будем подробно останавливаться на том, как это сделать. Этот момент подробно описан в уроке действия с десятичными дробями, в теме деление меньшего числа на большее. Продвинутый уровень.
Видно, что мы постоянно получаем остаток 1, далее приписываем к нему 0 и делим 10 на 3. И это повторяется вновь и вновь. В результате в дробной части каждый раз получается цифра 3. Деление 1 на 3 будет выполняться бесконечно, поэтому разýмнее будет остановиться на достигнутом.
Такие дроби называют периодическими, поскольку у них присутствует период цифр, который бесконечно повторяется. Период цифр может состоять из нескольких цифр, а может состоять из одной как в нашем примере.
В примере, который мы рассмотрели выше, период в дроби 0,33333 это цифра 3. Обычно такие дроби записывают сокращённо. Сначала записывают цéлую часть, затем ставят запятую и в скобках указывают период (цифру, которая повторяется).
В нашем примере повторяется цифра 3, она является периодом в дроби 0,33333. Поэтому сокращённая запись будет выглядеть так:
Читается как «ноль целых и три в периоде»
Пример 2. Разделить 5 на 11
Это тоже периодическая дробь. Период данной дроби это цифры 4 и 5, эти цифры повторяются бесконечно. Сокращённая запись будет выглядеть так:
Читается как «ноль целых и сорок пять в периоде»
Пример 3. Разделить 15 на 13
Здесь период состоит из нескольких цифр, а именно из цифр 153846. Для наглядности период отделён синей линией. Сокращённая запись для данной периодической дроби будет выглядеть так:
Читается как: «одна целая сто пятьдесят три тысячи восемьсот сорок шесть в периоде».
Пример 4. Разделить 471 на 900
В этом примере период начинается не сразу, а после цифр 5 и 2. Сокращённая запись для данной периодической дроби будет выглядеть так:
Читается как: «ноль целых пятьдесят две сотых и три в периоде».
Виды периодических дробей
Периодические дроби бывают двух видов: чистые и смéшанные.
Если в периодической дроби период начинается сразу после запятой, то такую периодическую дробь называют чистой. Например, следующие периодические дроби являются чистыми:
Видно, что в этих дробях период начинается сразу после запятой.
Если же в периодической дроби период начинается не сразу, а после некоторого количества не повторяющихся цифр, то такую периодическую дробь называют смéшанной. Например, следующие периодические дроби являются смéшанными:
Видно, что в этих дробях период начинается не сразу, а после некоторого количества не повторяющихся цифр.
Избавляемся от хвоста
Подобно тому, как ящерица избавляется от хвоста, мы можем избавить периодическую дробь от повторяющегося периода. Для этого достаточно округлить эту периодическую дробь до нýжного разряда.
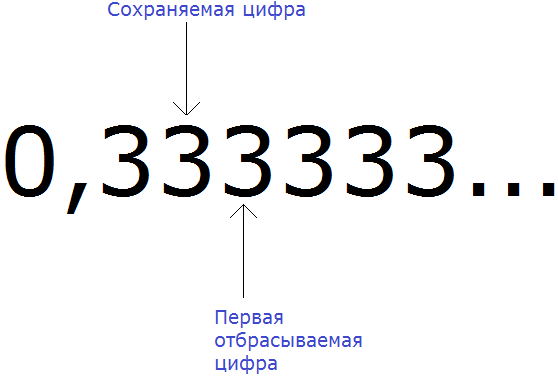
Например, округлим периодическую дробь 0, (3) до разряда сотых. Чтобы увидеть сохраняемую и отбрасываемую цифру, временно запишем дробь 0, (3) не в сокращённом виде, а в полном:
Вспоминаем правило округления. Если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.
Значит периодическая дробь 0, (3) при округлении до сотых обращается в дробь 0,33
Округлим периодическую дробь 6,31 (6) до разряда тысячных.
Запишем эту дробь в полном виде, чтобы увидеть сохраняемую и отбрасываемую цифру:
Вспоминаем правило округления. Если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.
Значит периодическая дробь 6,31 (6) при округлении до тысячных обращается в дробь 6,317
Перевод чистой периодической дроби в обыкновенную дробь
Перевод периодической дроби в обыкновенную это операция, которую мы будем применять довольно редко. Тем не менее, для общего развития желательно изучить и этот момент. А начнём мы с перевода чистой периодической дроби в обыкновенную дробь.
Мы уже говорили, что если период в периодической дроби начинается сразу после запятой, то такую дробь называют чистой.
Чтобы перевести чистую периодическую дробь в обыкновенную дробь, нужно в числитель обыкновенной дроби записать период периодической дроби, а в знаменатель обыкновенной дроби записать некоторое количество девяток. При этом, количество девяток должно быть равно количеству цифр в периоде периодической дроби.
В качестве примера, рассмотрим чистую периодическую дробь 0, (3) — ноль целых и три в периоде. Попробуем перевести её в обыкновенную дробь.
Правило гласит, что в первую очередь в числитель обыкновенной дроби нужно записать период периодической дроби.
Итак, записываем в числителе период дроби 0, (3) то есть тройку:
А в знаменатель нужно записать некоторое количество девяток. При этом, количество девяток должно быть равно количеству цифр в периоде периодической дроби 0, (3).
В периодической дроби 0, (3) период состоит из одной цифры 3. Значит в знаменателе обыкновенной дроби записываем одну девятку:
Полученную дробь 
Получили обыкновенную дробь 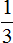
Таким образом, при переводе периодической дроби 0, (3) в обыкновенную дробь получается
Пример 2. Перевести периодическую дробь 0, (45) в обыкновенную дробь.
Здесь период составляет две цифры 4 и 5. Записываем эти две цифры в числитель обыкновенной дроби:
А в знаменатель записываем некоторое количество девяток. Количество девяток должно быть равно количеству цифр в периоде периодической дроби 0, (45).
В периодической дроби 0, (45) период состоит из двух цифр 4 и 5. Значит в знаменателе обыкновенной дроби записываем две девятки:
Полученную дробь 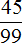
Таким образом, при переводе периодической дроби 0, (45) в обыкновенную дробь получается
Перевод смешанной периодической дроби в обыкновенную дробь
Чтобы перевести смешанную периодическую дробь в обыкновенную дробь, нужно в числителе записать разность в которой уменьшаемое это цифры, стоящие после запятой в периодической дроби, а вычитаемое — цифры, стоящие между запятой и первым периодом периодической дроби.
В знаменателе же нужно записать некоторое количество девяток и нулей. При этом, количество девяток должно быть равно количеству цифр в периоде периодической дроби, а количество нулей должно быть равно количеству цифр между запятой и периодом периодической дроби.
Например, переведём смешанную периодическую дробь 0,31 (6) в обыкновенную дробь.
Сначала запишем в числителе разность. Уменьшаемым будут все цифры, стоящие после запятой (включая и период), а вычитаемым будут цифры, стоящие между запятой и периодом:
Итак, записываем в числителе разность:
А в знаменателе запишем некоторое количество девяток и нулей. Количество девяток должно быть равно количеству цифр в периоде периодической дроби 0,31 (6)
В дроби 0,31 (6) период состоит из одной цифры. Значит в знаменатель дроби записываем одну девятку:
Теперь дописываем количество нулей. Количество нулей должно быть равно количеству цифр между запятой и периодом периодической дроби.
В дроби 0,31 (6) между запятой и периодом располагается две цифры. Значит в знаменателе дроби должно быть два нуля. Дописываем их:
Получили выражение, которое вычисляется легко:
Получили ответ
Таким образом, при переводе периодической дроби 0,31 (6) в обыкновенную дробь, получается
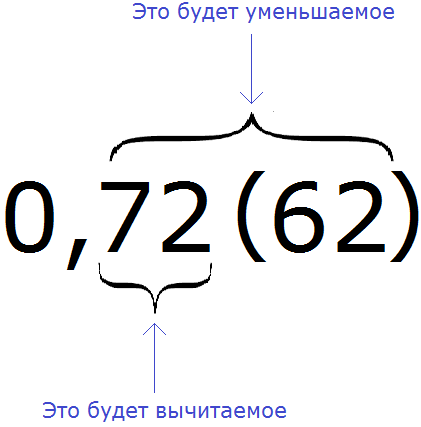
Пример 2. Перевести смешанную периодическую дробь 0,72 (62) в обыкновенную дробь
Сначала запишем в числителе разность. Уменьшаемым будут все цифры, стоящие после запятой (включая и период), а вычитаемым будут цифры, стоящие между запятой и периодом:
Итак, записываем в числителе разность:
А в знаменателе запишем некоторое количество девяток и нулей. Количество девяток должно быть равно количеству цифр в периоде периодической дроби 0,72 (62)
В дроби 0,72 (62) период состоит из двух цифр. Значит в знаменатель дроби записываем две девятки:
Теперь дописываем количество нулей. Количество нулей должно быть равно количеству цифр между запятой и периодом периодической дроби.
В дроби 0,72 (62) между запятой и периодом располагаются две цифры. Значит в знаменателе дроби должно быть два нуля. Дописываем их:
Получили выражение, которое вычисляется легко:
Получили ответ
Значит при переводе периодической дроби 0,72 (62) в обыкновенную дробь, получается
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
34 thoughts on “Периодические дроби”
Когда же следующие уроки? Уже что-то долго ничего нету
Большое спасибо за урок! Откровенно говоря…эту тему не помню вообще…Будто ее и не было в школе О__о Ну или я ее проболела… (Перевод смешанной периодической дроби в обыкновенную дробь)
Вы бы хоть номер кошелька написали. А то столько трудились и никакой отдачи. С такими уроками никакой экзамен не страшен.
Спасибо большое Тэла, за столь добрый отзыв ?
Если люди получают пользу от этих уроков — это уже отдача)
Огромное Вам спасибо за уроки! Всё объясняете доступно и наглядно! На ваших уроках готовлюсь поступать на ФИТ на программиста. Хорошо бы еще алгебру выложили.)
Вы не могли бы объяснить логику алгоритма перевода периодической дроби в обычную?
Зачем в знаменателе ставятся девятки — заместно, например, округления числа, подставляемого в числитель, до последней цифры периода, и постановки степени 10 в знаменатель? Зачем, при переводе смешанной периодической дроби, производится соотв. вычитание и чем объясняется подстановка нулей и единиц в зависимости от принадлежности цифры к периоду??…
Спасибо большое за урок ? Скажите пожалуйсто при округлении(когда избавляемся от хвоста) откуда знать до каких разряд надо округлять?
Вот и здесь последняя задача говорит округлить до разряда сотых,а почему не до десятых(например)?
зависит от задачи, которую решаете. Если в задаче сказано округлять до десятых, значит округляете до десятых. Если сказано округлять до сотых — округляете до сотых
Источник
период
Его стихи, романы и автобиографические книги повествуют о разных периодах его карьеры искателя приключений, авиатора, журналиста и поэта.
О минувших периодах истории мы судим по сохранившимся до наших дней памятникам культуры.
Период вращения этого спутника вокруг оси равен периоду его обращения вокруг Земли.
Полезное
Смотреть что такое «период» в других словарях:
Период — (греч. periodos «обход», «окружность») термин, введенный Аристотелем для обозначения «речи, имеющей в себе самой начало и конец и легко обнимаемой умом». Под П. следует понимать так. обр. большую синтаксическую единицу, сложное предложение или… … Литературная энциклопедия
ПЕРИОД — периода, м. [греч. periodos] (книжн.). 1. Промежуток времени, в течение к–рого заканчивается какой–н. повторяющийся процесс (науч.). Синодический период обращения планеты (время, в течение к–рого планета совершает один полный оборот вокруг… … Толковый словарь Ушакова
Период — ПЕРИОД (Περιοδος обход, окружность). Этим словом в древней Греции называлась та замкнутая, кольцевая дорога, на которой происходили игры и состязания во время олимпийских празднеств. Этим термином Аристотель стал обозначать особый вид… … Словарь литературных терминов
ПЕРИОД — (греч. periodos путь кругом). 1) промежуток времени между двумя важными историческими событиями. 2) в астрономии то же, что цикл; в арифметике: число цифр, повторяющихся, в том же порядке, бесчисленное множество раз. 3) особенно развитое сложное… … Словарь иностранных слов русского языка
период — а, м. période f. <лат. periodus<гр. periodos обход, круговращение, орбита небесного тела. 1. Промежуток времени, в который протекает та или иная часть общего процесса. БАС 1. Бывают в жизни его периоды во время которых выступает он из… … Исторический словарь галлицизмов русского языка
ПЕРИОД — муж. срок или промежуток времени, продолжительность; время от одного события до другого. История делится на периоды, сроки. Период первозданный период осадочный, сроки образованья земной толщи. | Длительность самого события, действия, состоянья;… … Толковый словарь Даля
ПЕРИОД — (1) промежуток времени, в течение которого начинается, развивается и заканчивается какой либо процесс; наименьший интервал времени, по истечении которого произвольно выбранные мгновенные значения периодической величины повторяются; (2) П. в… … Большая политехническая энциклопедия
Период С — Студийный а … Википедия
ПЕРИОД — срок протекания экономического процесса, действия, плана, договора, гарантии, уплаты долгов, внесения налогов, выполнения работ (гарантийный период, плановый период, период обложения, период окупаемости). Райзберг Б.А., Лозовский Л.Ш.,… … Экономический словарь
период — См … Словарь синонимов
ПЕРИОД — колебаний, наименьший промежуток времени, через который совершающая колебания система возвращается в то же состояние, в котором она находилась в начальный момент, выбранный произвольно. Период величина, обратная частоте колебаний. Понятие период… … Современная энциклопедия
Источник
Значение слова «период»
2. Спец. Промежуток времени, в течение которого заканчивается какой-л. повторяющийся процесс. Период колебания.
3. Геол. Промежуток времени, в течение которого образовались горные породы определенной геологической системы отложений; часть эры, делящаяся в свою очередь на эпохи. Каменноугольный период палеозойской эры.
4. Мат. Группа повторяющихся цифр в бесконечной десятичной дроби.
5. Грамм. Сложное синтаксическое целое, состоящее из одного сложного предложения или из соединения нескольких предложений, части которого связаны между собой грамматически, лексически и интонационно.
Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека
В физике, астрономии:
Период колебаний — время (в секундах) между двумя последовательными прохождениями тела через одно и то же положение в одном и том же направлении, величина, обратная частоте.
Период полураспада — время, за которое число ядер данного изотопа уменьшается в два раза.
Период периодической системы — строка периодической таблицы, объединяющая элементы с одинаковым числом электронных оболочек.
В хронологии (истории, археологии, палеонтологии) — единица хронологической классификации: выделенный в прошлом промежуток времени связанный с некими событиями или обладающий некими характерными особенностями.
Период (риторика) — пространное предложение, отличающееся полнотой развёртывания мысли и законченностью интонации.
В хоккее с шайбой или пляжном футболе — одна из трёх частей матча.
ПЕРИ’ОД, а, м. [греч. periodos] (книжн.). 1. Промежуток времени, в течение к-рого заканчивается какой-н. повторяющийся процесс (науч.). Синодический п. обращения планеты (время, в течение к-рого планета совершает один полный оборот вокруг Солнца; астр.). П. колебательного движения (время, в течение которого тело возвращается в исходное положение; физ.). 2. Промежуток времени, противопоставляемый другим, определенный срок, в течение к-рого что-н. происходило, произошло. Одесский п. жизни Пушкина. В течение долгого периода был учителем. В п. подготовки чего-н. || Промежуток времени, характеризующийся тем или иным социально-политическим, культурно-историческим явлением, отдельная часть какого-н. исторического процесса. . Мы имеем теперь последний период НЭП<>‘а, конец НЭП’а, период полной ликвидации капитализма во всех сферах народного хозяйства. Сталин (доклад на Чрезвычайном VIII Всесоюзном съезде советов 25/XI 1936 г.). П. военного коммунизма. П. нэпа. Реконструктивный п. Классический п. русской литературы. 3. Часть эры, делящаяся в свою очередь на эпохи (геол.). Пермский п. палеозойской эры. Верхняя эпоха мелового периода мезозойской эры.
4. Промежуток времени, в течение которого заканчивается какой-н. процесс (науч.). Инкубационный п. болезни. 5. Величина, выражающая промежуток, через который повторяется значение функции (мат.). 6. Группа повторяющихся цифр в бесконечной десятичной дроби (мат.). 7. Сложное синтаксическое построение для подробного развития мысли (предложение, распространенное многими второстепенными членами или многими придаточными предложениями, или же соединение многих равносильных предложений), употребляемое как стилистический прием с целью благозвучия, к-рое достигается ритмическим расположением частей, повышением и понижением голоса (лит.). Простой п. (с одним главным предложением). Сложный п. (со многими главными предложениями). || Неточно — вообще длинное синтаксическое целое, длинная фраза из многих предложений и т. п. (разг.). Пишите короче, избегайте периодов.
Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека
пери́од
1. отрезок времени, в течение которого циклический процесс совершает полный цикл изменений ◆ Ряд явлений на Земле повторяется с периодом вращения Солнца (около 27 дней). ◆ Цикл измерений повторяется с периодом 1 сек.
2. отрезок времени как этап, стадия какого-либо процесса ◆ Послевоенное время стало для неё периодом небывалого успеха. ◆ Принято считать, что в советский период русская философия не имела никаких перспектив для своего развития. ◆ Был у меня период в жизни, когда я подсел на кофе, почти как наркоман.
3. спорт. отдельная, изолированная часть матча в хоккее и некоторых других командных играх ◆ Первый период наша команда имела преимущество; во втором периоде было очень много удалений; что в свою очередь поломало игру, третий период нащи хоккеисты играли строго в обороне, старались не позволить сопернику выходить на активные зоны.
4. матем. ненулевая величина (обычно наименьшая положительная), прибавление которой к аргументу периодической функции не изменяет значений этой функции ◆ Хорошим примером периодических функций могут служить тригонометрические функции y = sin x, y = cos x (период этих функций равен 2π).
5. матем. бесконечно повторяющаяся последовательность цифр после запятой в позиционной записи рационального числа ◆ При делении в столбик 1 на 7 встретятся все остатки от 1 до 6, а в периоде будет шестизначное число 142857.
6. устар. лингв. то же, что предложение ◆ Точка заключает целый период, и ей обыкновенно следует прописная буква, которою также имена почтенные и собственные начинаются. М. В. Ломоносов, «Российская грамматика», 1755 г. (цитата из НКРЯ)
7. геол. промежуток времени, в течение которого отложился слой пород, образующих соответствующую геологическую систему ◆ Еще в юрский период в Центральной Азии были многочисленные озера и на их берегах пышная растительность, судя по присутствию пластов угля в юрских толщах. В. А. Обручев, «В дебрях Центральной Азии», 1951 г. (цитата из НКРЯ)
Источник
Теперь вы знаете какие однокоренные слова подходят к слову Как пишется период в математике, а так же какой у него корень, приставка, суффикс и окончание. Вы можете дополнить список однокоренных слов к слову «Как пишется период в математике», предложив свой вариант в комментариях ниже, а также выразить свое несогласие проведенным с морфемным разбором.
Определение
Бесконечная десятичная дробь, у которой одна или несколько цифр повторяются в одной и той же
последовательности, называется периодической десятичной дробью.
Например. $0,1234444444 ldots ; 12,453737373737 ldots$
Повторяющиеся цифры — период — для сокращения записи пишут в круглых скобках.
Например. $0,12344444444 ldots=0,123(4)$ ;
$12,453737373737 ldots=12,45(37)$
Определение
Чистой периодической дробью называется периодическая дробь, у которой период начинается сразу после запятой.
Например. $2,4949 ldots=2,(49)$
Определение
Смешанной периодической дробью называется такая десятичная дробь, у которой между запятой и
периодом есть не менее одной неповторяющейся бесконечное число раз цифры.
Например. $0,11232323 ldots=0,11(23)$ ;
$1,54444 . .=1,5(4)$
Чтобы обратить чистую периодическую дробь в обыкновенную, достаточно записать числителем ее период,
а в знаменателе записать столько девяток, сколько цифр в периоде.
Чтобы записать смешанную периодическую дробь в виде обыкновенной, надо из числа, стоящего до второго
периода вычесть число, стоящее до первого периода, результат записать в
числителе; в
знаменатель записать
число, содержащее столько девяток, сколько цифр в периоде, и столько нулей в конце, сколько цифр между
запятой и периодом.
Например. Запишем дробь $2,34(2)$ в виде обыкновенной
Читать первую тему — понятие дроби и виды дробей,
раздела дроби.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Plan
- 1 Что такое число в периоде?
- 2 Как записать число в периоде?
- 3 Как называются цифры после запятой?
- 4 Как называется число с бесконечным числом после запятой?
- 5 Сколько цифр после запятой в десятичной дроби?
- 6 Что такое десятичное число?
- 7 Как перевести сумму в тысячные?
- 8 Что больше десятые сотые или тысячные?
- 9 Что значит округлить до сотых?
- 10 Как правильно округлить число до десятков?
- 11 Как правильно округлять десятичные числа?
- 12 Как округлить число?
- 13 Как округлять с 5?
- 14 Как округлить миллионы до тысяч?
- 15 Как округлить до двух знаков после запятой?
- 16 Как округляются отрицательные числа?
- 17 Что такое округление чисел?
- 18 Как округлить число до 1000?
- 19 Как в Excel округлить в меньшую сторону?
- 20 Как в Питоне округлить в большую сторону?
Что такое число в периоде?
Повторяющуюся группу цифр после запятой называют периодом, а саму десятичную дробь — бесконечной десятичной периодической дробью. Число 7 также можно представить в виде бесконечной десятичной периодической дроби.
Как записать число в периоде?
Обычно такие дроби записывают сокращённо. Сначала записывают цéлую часть, затем ставят запятую и в скобках указывают период (цифру, которая повторяется). Читается как: «одна целая сто пятьдесят три тысячи восемьсот сорок шесть в периоде». Читается как: «ноль целых пятьдесят две сотых и три в периоде».
Что значит дробь в периоде?
Если в записи десятичной дроби одна цифра или группа цифр начинают повторяться бесконечно много раз, такую дробь называют периодической дробью. В краткой записи периодической дроби повторяющуюся цифру (или группу цифр) пишут в скобках. Эту цифру (или группу цифр) называют периодом дроби.
Как называются цифры после запятой?
— десятичные цифры. Причём последовательность цифр до запятой (слева от неё) конечна (как минимум одна цифра), а после запятой (справа от неё) — может быть как конечной (в частности, цифры после запятой могут вообще отсутствовать), так и бесконечной.
Как называется число с бесконечным числом после запятой?
Если последовательность цифр после запятой является бесконечной, то десятичная дробь называется бесконечной. называется периодической. Такая запись означает, что последовательность цифр после запятой, начиная с некоторого номера, включает в себя повторяющуюся группу цифр.
Как правильно читать цифры после запятой?
Десятые, сотые и тысячные Чтобы правильно прочитать десятичную дробь нужно: Прочитать число слева от запятой и добавить слово «целыx», так как слева от запятой находится целая часть десятичной дроби. Читаем: «сорок три целых». Затем прочитать число справа от запятой: «семь тысяч пятьсот шестьдесят девять».
Сколько цифр после запятой в десятичной дроби?
Десятичная дробь, как и любое число, состоит из цифр (0, 1, 2, 3, 4, 5, 6, 7, 8, 9). Место каждой цифры в числе важно: оно определяет разряд числа. Десятичная дробь состоит из целой части (все цифры до запятой) и дробной части (все цифры после запятой).
Что такое десятичное число?
Десятичное число — основной тип данных ЭКВМ. Используется для хранения в десятичных регистрах как целых чисел (англ. integer), так чисел с естественной (десятичные дроби) и плавающей запятой (англ. При вводе и выводе десятичных чисел в качестве разделителя целой и дробной части числа используется десятичная запятая.
Как тысячные перевести в сотые?
Чтобы округлить данное число до сотых, после запятой оставим лишь две цифры, а остальные — отбросим. Первая из отброшенных цифр равна 5, поэтому предыдущую цифру увеличиваем на единицу. Читают: «Нуль целых тысяча двести пятьдесят четыре тысячных приближенно равно нуль целых тринадцать сотых».
Как перевести сумму в тысячные?
Чтобы перевести числа в тысячи, нужно эти числа разделить на тысячу.
Что больше десятые сотые или тысячные?
Если десятые части равны, сравнить сотые части. То число, у которого сотых частей больше, и будет больше. То число, у которого тысячных частей больше, и будет больше.
Как перевести сотые в десятые?
Чтобы округлить до десятых, нужно убрать после запятой все цифры, кроме одной. Если следующая после остающейся цифра 0, 1, 2, 3 или 4, то цифру не изменяем. Если следующая после остающейся — 5, 6, 7, 8 или 9, то цифру увеличиваем на единицу. С сотыми по тому же принципу, только после запятой оставляем 2 цифры.
Что значит округлить до сотых?
Чтобы округлить число до сотых, надо оставить после запятой две цифры, а остальные отбросить. Если первая отброшенная цифра 0, 1, 2, 3 или 4, то предыдущая цифра не изменится. Если первая из отброшенных цифр 5, 6, 7, 8 или 9, то предыдущую цифру нужно увеличить на единицу.
Как правильно округлить число до десятков?
Правило округления числа до десятков Чтобы округлить число до десятков, нужно цифру в разряде единиц заменить нулем, а если в записи числа есть цифры после запятой, то их следует отбросить.
Как округлить до единиц десятичную дробь?
Если десятичную дробь требуется округлить до целого числа (до единиц), смотрим на цифру, которая идет сразу же после запятой (разряд – десятые). Если это 5, 6, 7, 8 или 9, то к единицам в целой части прибавляем число 1, а всю дробную часть отбрасываем.
Как правильно округлять десятичные числа?
Отделите все цифры, стоящие справа. Если справа от цифры, которую нужно округлить, стоит 0, 1, 2, 3 или 4 — цифра остается без изменений. Отбросьте все цифры справа от цифры округляемого разряда. Если справа от цифры округляемого разряда стоит 5, 6, 7, 8 или 9 — к цифре округляемого разряда прибавляем один.
Как округлить число?
Чтобы округлить натуральное число, нужно в записи числа выбрать разряд, до которого производится округление. Цифра, записанная в выбранном разряде: не меняется, если следующая за ней справа цифра — 0, 1, 2, 3 или 4; увеличивается на единицу, если следующая за ней справа цифра — 5,6,7,8 или 9.
Как округлить десятичную дробь до целых?
Чтобы округлить число до целого (или округлить число до единиц), надо отбросить запятую и все числа, стоящие после запятой. Если первая из отброшенных цифр 0, 1, 2, 3 или 4, то число не изменится. Если первая из отброшенных цифр 5, 6, 7, 8 или 9, предыдущую цифру нужно увеличить на единицу.
Как округлять с 5?
Если отсекается цифра 5 , а за ней не имеется значащих цифр, то округление выполняется на ближайшее четное число, другими словами, последняя оставляемая цифра остаётся неизменной, если она четная, и усиливается в случае, если она нечетная. Число 0,0465 округлённо записывается как – 0,046 .
Как округлить миллионы до тысяч?
(1) Для округления чисел до тысяч используйте эту формулу = ОКРУГЛ (A2; -3); для округления чисел до сотен используйте эту формулу = ОКРУГЛ (A2; -2). (2) Для округления чисел до миллионов используйте эту формулу = ОКРУГЛВВЕРХ (A2; -6); для округления чисел до миллионов используйте эту формулу = ОКРУГЛ ВНИЗ (A2; -6).
Что значит округлить до целого числа?
Округлить до целых – значит заменить десятичную дробь ближайшим к ней целым числом. 1) Например, десятичную дробь 4,2 мы хотим округлить до целых. Очевидно, что 4 < 4,2 < 5. К какому из целых чисел – к числу 4 или число 5 – находится ближе наша десятичная дробь?
Как округлить до двух знаков после запятой?
Как правило, округление до 2 знаков после запятой очень легко с помощью printf(%. 2lf,); Однако система округления обычно округляется до ближайшего четного . Например, 2.554 -> 2.55 2.555 -> 2.56 2.565 -> 2.56 2.566 -> 2.57 И вот чего я хочу добиться 2.555 -> 2.56…
Как округляются отрицательные числа?
По умолчанию отрицательные числа с десятичными знаками округляются до целого числа в меньшую сторону (дальше от нуля). Например, -4,7 округляется до -5.
Как математически округлить число?
В общем случае, когда число в десятичной системе округляют до N-го знака, правило может быть сформулировано следующим образом:
- если N+1 знак < 5, то N-й знак сохраняют, а N+1 и все последующие обнуляют;
- если N+1 знак ≥ 5, то N-й знак увеличивают на единицу, а N+1 и все последующие обнуляют;
Что такое округление чисел?
Округлить число до определенной цифры (знака), значит заменить его близким по значению числом с нулями на конце. Если число округляется до десятков, то нулями заменяем цифру в разряде единицы. Если число округляется до сотен, то цифра ноль должна стоять и в разряде единиц, и в разряде десятков.
Как округлить число до 1000?
Правило округления числа до тысячных Чтобы округлить десятичную дробь до тысячных, надо оставить после запятой только три цифры, а остальные следующие за ней цифры отбросить. Если первая из отброшенных цифр 0,1,2,3 или 4, то предыдущую цифру оставляем без изменений.
Как округлить в большую сторону?
Чтобы округление всегда выполнялось в большую по модулю сторону, используйте функцию ОКРУГЛВВЕРХ. Чтобы округление всегда выполнялось до ближайшего меньшего по модулю, используйте функцию ОКРУГЛВНИЗ. Чтобы число округлялось с нужной кратностью (например, до ближайшего числа, кратного 0,5), используйте функцию ОКРУГЛТ.
Как в Excel округлить в меньшую сторону?
Формула: =ОКРУГЛВВЕРХ(A1;0). Чтобы округлить в меньшую сторону в Excel, применяется функция «ОКРУГЛВНИЗ». Пример формулы: =ОКРУГЛВНИЗ(A1;1). Формулы «ОКРУГЛВВЕРХ» и «ОКРУГЛВНИЗ» используются для округления значений выражений (произведения, суммы, разности и т.
Как в Питоне округлить в большую сторону?
Сделать это можно, например, с помощью инструкции: import math .
- math. ceil() — округление чисел в большую сторону
- math. floor() — округление чисел в меньшую сторону
- math. trunc() — отбрасывание дробной части
- Нормальное округление
- round() — округление чисел
Как в Excel округлять до большего?
Функция ОКРУГЛВВЕРХ подобна функции ОКРУГЛ с той разницей, что округление всегда производится с избытком. Если число_разрядов больше 0, то число округляется с избытком до заданного количества десятичных разрядов после десятичной запятой. Если число_разрядов равно 0, то число округляется до ближайшего целого.
ПЕРИОД
- ПЕРИОД
-
функции f(x) — число
такое, что при любом
(или
) числа х-Т и x+Ттакже принадлежат множеству X и выполняется равенство
Числа + пТ, где п — любое натуральное число, также являются П. функции f(x). У функции f=const на оси или на плоскости любое число
будет П.; для функции Дирихле
любое рациональное число
будет П. Если функция f(x).имеет период Т, то функция
,
где аи b — постоянные и
, имеет период
. Если действительная функция f(x). с действительным аргументом непрерывна на X(и не равна тождественно постоянной), то она имеет наименьший период T0>0 и всякий другой действительный П. кратен Т 0. Существуют функции с комплексным аргументом, у к-рых имеются два некратных с мнимым частным П.; таковы, напр., эллиптические функции.
Аналогично определяется П. функции, определенной на нек-рой абелевой группе. А. А. Конюшков.
Математическая энциклопедия. — М.: Советская энциклопедия.
.
1977—1985.
Синонимы:
Полезное
Смотреть что такое «ПЕРИОД» в других словарях:
-
Период — (греч. periodos «обход», «окружность») термин, введенный Аристотелем для обозначения «речи, имеющей в себе самой начало и конец и легко обнимаемой умом». Под П. следует понимать так. обр. большую синтаксическую единицу, сложное предложение или… … Литературная энциклопедия
-
ПЕРИОД — периода, м. [греч. periodos] (книжн.). 1. Промежуток времени, в течение к–рого заканчивается какой–н. повторяющийся процесс (науч.). Синодический период обращения планеты (время, в течение к–рого планета совершает один полный оборот вокруг… … Толковый словарь Ушакова
-
Период — ПЕРИОД (Περιοδος обход, окружность). Этим словом в древней Греции называлась та замкнутая, кольцевая дорога, на которой происходили игры и состязания во время олимпийских празднеств. Этим термином Аристотель стал обозначать особый вид… … Словарь литературных терминов
-
ПЕРИОД — (греч. periodos путь кругом). 1) промежуток времени между двумя важными историческими событиями. 2) в астрономии то же, что цикл; в арифметике: число цифр, повторяющихся, в том же порядке, бесчисленное множество раз. 3) особенно развитое сложное… … Словарь иностранных слов русского языка
-
период — а, м. période f. <лат. periodus<гр. periodos обход, круговращение, орбита небесного тела. 1. Промежуток времени, в который протекает та или иная часть общего процесса. БАС 1. Бывают в жизни его периоды во время которых выступает он из… … Исторический словарь галлицизмов русского языка
-
ПЕРИОД — муж. срок или промежуток времени, продолжительность; время от одного события до другого. История делится на периоды, сроки. Период первозданный период осадочный, сроки образованья земной толщи. | Длительность самого события, действия, состоянья;… … Толковый словарь Даля
-
ПЕРИОД — (1) промежуток времени, в течение которого начинается, развивается и заканчивается какой либо процесс; наименьший интервал времени, по истечении которого произвольно выбранные мгновенные значения периодической величины повторяются; (2) П. в… … Большая политехническая энциклопедия
-
Период С — Студийный а … Википедия
-
ПЕРИОД — срок протекания экономического процесса, действия, плана, договора, гарантии, уплаты долгов, внесения налогов, выполнения работ (гарантийный период, плановый период, период обложения, период окупаемости). Райзберг Б.А., Лозовский Л.Ш.,… … Экономический словарь
-
период — См … Словарь синонимов
-
ПЕРИОД — колебаний, наименьший промежуток времени, через который совершающая колебания система возвращается в то же состояние, в котором она находилась в начальный момент, выбранный произвольно. Период величина, обратная частоте колебаний. Понятие период… … Современная энциклопедия
Как правильно писать временные периоды и числовые интервалы? Где нужно тире, где – дефис (он немного короче), а где их использование ошибочно? Когда уместен буквенно-числовой способ указания периода, а когда можно и одними цифрами обойтись? Как правильно использовать и понимать сокращения типа «г.», «гг.», «н.э.» и др.?
Если числовой интервал представлен цифрами, которые следуют одна за другой, используется дефис, например, 1-2 дня, 5-6 вариантов. Правило гласит, что дефис между числительными пишется в том случае, если между ними по смыслу можно поставить союз «или»: один или два дня.
Если же числовой интервал предполагает пропуск хотя бы одной цифры или показателя, используем тире (без пробелов): 1–3 дня, 10–15 процентов. В данном случае союз «или» по смыслу не подходит, т.к. имеется в виду интервал, который можно представить предлогами «с… по», «с… до», «от… до»: от одного до трех дней. Так же поступаем и с дробными числительными: в 1,5–1,7 раза.
Еще один вариант: интервал значений представлен словами (что встречается гораздо реже). Тогда мы используем те же знаки, что и для чисел:
- тире с пробелами, например, тридцать – тридцать пять человек;
- дефис – во фразах типа один-два, три-четыре.
Используются тире и дефисы и в датах. Через тире и без пробелов должен быть записан временной интервал типа 2010–2014 гг. и через дефис 2010-2011 гг., потому что в первом случае во временном отрезке пропущено несколько лет, а во втором годы следуют один за другим. Попутно заметим, что написание даты типа 2010–14 не принято, а слово «года» уместно заменять сокращением «гг.».
Одновременное использование и тире, и дефиса будет оправданным в написаниях типа 70–80-е годы. Обратите внимание, что окончание (-е) пишется только у последнего числительного, поскольку окончания обоих числительных совпадают (семидесятые, восьмидесятые).
Довольно часто встречаются ошибки в написании сложных слов, одна часть которых представлена числительными. Как только ни пишут: и 50-тилетний, и 50-ти летний, и 50-ти-летний! А как надо? Если первую часть слова мы пишем цифрой (50), то после дефиса остается последнее слово (-летний), т.е. должно получиться 50-летний, 25-процентный, 12-метровый. И постарайтесь избегать написаний типа 1-местный или 2-разовый: числа до 10 лучше записать словами (одноместный, двухразовый).
Теперь – о том, когда ни тире, ни дефис лучше не употреблять:
- в числовых интервалах дат, представленных цифрами (дд.мм.гггг). В данном случае лучше использовать предлоги: с 23.07.2014 по 30.08.2014. При этом некорректно писать, например, с 23.07 по 30.08.2014, 23.07–30.08.2014 или с 11 по 15.08.2014. В таком случае названия месяцев лучше писать словами: с 23 июля по 30 августа 2014 г. или с 11 по 15 августа 2014 г.;
- в количественных числительных (правильно: работа 12 сотрудников, неправильно: работа 12-ти сотрудников);
- при записи календарных дат (правильно: 15 августа 2014 года, неправильно: 15-е августа 2014 года);
- при обозначении чисел римскими цифрами (правильно: VII всероссийская конференция, неправильно: VII-я всероссийская конференция).
Не забудем и о том, что если день в дате представлен простым числительным до 10, то перед ним в документах лучше писать «0»: с 04 августа 2014 г., а не с 4 августа 2014 г. Считается, что это помешает «злоумышленникам» путем дописания новой цифры исправить дату, т.е. они не смогут превратить 4, например, в 14-е или 24-е число.
Распространенной ошибкой является появление «г.» после даты, написанной числовым способом (правильно: 01.08.2014, неправильно: 01.08.2014 г., ведь здесь год является составной частью указания конкретной даты).
Примечательно, но казусы случаются не только с правильным написанием временных периодов, но и с их правильным пониманием. А причина кроется в том, что историческая наука, похоже, самая «политическая», ведь новые победители часто переписывают ее, особенно при существенном изменении идеологии.
Вспомните сокращение «н.э.». Его используют, когда хотят сказать, что какие-то события происходили «до нашей эры», а какие-то – уже «в нашу эру». Но еще в начале 90-х мой преподаватель истории с сарказмом заметила: «Что это за «наша» эра такая? И если это – «наша», то какая тогда «не наша»?» – и строго-настрого наказала нам говорить «до новой эры», «новая эра».
А «появилась» эта эра в России после революции, когда новая власть не могла позволить людям продолжать писать 1917 г. от Р.Х. или 324 г. до Р.Х., что означало, соответственно, 1917 г. от Рождества Христова и 324 г. до этого знакового события. Вот и приучили нас писать 324 г. до н.э.
Но в отечественной истории были и более кардинальные изменения в летоисчислении, смена координат часто становится необходимой для смены мировоззрения народа. Так, с 1 января 1700 года по указу Петра I Россия перешла на новое «западноевропейское» летоисчисление, предыдущий год датировался у нас не 1699 годом, а 7208 – на тот момент нашими предками уже было отсчитано несколько тысяч лет!
В древних документах часто встречается формулировка даты от сотворения мира (и нас в школе успели приучить к мысли, что имеется в виду сотворение мира Богом). Но в последнее время набирает обороты версия о том, что наши предки вели отсчет от некоего знакового события, о котором они еще помнили (а мир, по их мнению, был сотворен Богом еще раньше). Речь идет о сотворении мира в звездном храме, т.е. о подписании мирного договора после большой войны.
Периодические десятичные дроби
10 февраля 2012
Помните, как в самом первом уроке про десятичные дроби я говорил, что существуют числовые дроби, не представимые в виде десятичных (см. урок «Десятичные дроби»)? Мы еще учились раскладывать знаменатели дробей на множители, чтобы проверить, нет ли там чисел, отличных от 2 и 5.
Так вот: я наврал. И сегодня мы научимся переводить абсолютно любую числовую дробь в десятичную. Заодно познакомимся с целым классом дробей с бесконечной значащей частью.
Периодическая десятичная дробь — это любая десятичная дробь, у которой:
- Значащая часть состоит из бесконечного количества цифр;
- Через определенные интервалы цифры в значащей части повторяются.
Набор повторяющихся цифр, из которых состоит значащая часть, называется периодической частью дроби, а количество цифр в этом наборе — периодом дроби. Остальной отрезок значащей части, который не повторяется, называется непериодической частью.
Поскольку определений много, стоит подробно рассмотреть несколько таких дробей:
Эта дробь встречается в задачах чаще всего. Непериодическая часть: 0; периодическая часть: 3; длина периода: 1.
Непериодическая часть: 0,58; периодическая часть: 3; длина периода: снова 1.
Непериодическая часть: 1; периодическая часть: 54; длина периода: 2.
Непериодическая часть: 0; периодическая часть: 641025; длина периода: 6. Для удобства повторяющиеся части отделены друг от друга пробелом — в настоящем решении так делать не обязательно.
Непериодическая часть: 3066; периодическая часть: 6; длина периода: 1.
Как видите, определение периодической дроби основано на понятии значащей части числа. Поэтому если вы забыли что это такое, рекомендую повторить — см. урок «Умножение и деление десятичных дробей».
Переход к периодической десятичной дроби
Рассмотрим обыкновенную дробь вида a/b. Разложим ее знаменатель на простые множители. Возможны два варианта:
- В разложении присутствуют только множители 2 и 5. Эти дроби легко приводятся к десятичным — см. урок «Десятичные дроби». Такие нас не интересуют;
- В разложении присутствует что-то еще, кроме 2 и 5. В этом случае дробь непредставима в виде десятичной, зато из нее можно сделать периодическую десятичную дробь.
Чтобы задать периодическую десятичную дробь, надо найти ее периодическую и непериодическую часть. Как? Переведите дробь в неправильную, а затем разделите числитель на знаменатель «уголком».
При этом будет происходить следующее:
- Сначала разделится целая часть, если она есть;
- Возможно, будет несколько чисел после десятичной точки;
- Через некоторое время цифры начнут повторяться.
Вот и все! Повторяющиеся цифры после десятичной точки обозначаем периодической частью, а то, что стоит спереди — непериодической.
Задача. Переведите обыкновенные дроби в периодические десятичные:

Все дроби без целой части, поэтому просто делим числитель на знаменатель «уголком»:
Как видим, остатки повторяются. Запишем дробь в «правильном» виде: 1,733 … = 1,7(3).
В итоге получается дробь: 0,5833 … = 0,58(3).
Записываем в нормальном виде: 4,0909 … = 4,(09).
Получаем дробь: 0,4141 … = 0,(41).
Переход от периодической десятичной дроби к обыкновенной
Рассмотрим периодическую десятичную дробь X = abc(a1b1c1). Требуется перевести ее в классическую «двухэтажную». Для этого выполним четыре простых шага:
- Найдите период дроби, т.е. подсчитайте, сколько цифр находится в периодической части. Пусть это будет число k;
- Найдите значение выражения X · 10k. Это равносильно сдвигу десятичной точки на полный период вправо — см. урок «Умножение и деление десятичных дробей»;
- Из полученного числа надо вычесть исходное выражение. При этом периодическая часть «сжигается», и остается обычная дробь;
- В полученном уравнении найти X. Все десятичные дроби переводим в обыкновенные.
Задача. Приведите к обыкновенной неправильной дроби числа:
- 9,(6);
- 32,(39);
- 0,30(5);
- 0,(2475).
Работаем с первой дробью: X = 9,(6) = 9,666 …
В скобках содержится лишь одна цифра, поэтому период k = 1. Далее умножаем эту дробь на 10k = 101 = 10. Имеем:
10X = 10 · 9,6666 … = 96,666 …
Вычитаем исходную дробь и решаем уравнение:
10X − X = 96,666 … − 9,666 … = 96 − 9 = 87;
9X = 87;
X = 87/9 = 29/3.
Теперь разберемся со второй дробью. Итак, X = 32,(39) = 32,393939 …
Период k = 2, поэтому умножаем все на 10k = 102 = 100:
100X = 100 · 32,393939 … = 3239,3939 …
Снова вычитаем исходную дробь и решаем уравнение:
100X − X = 3239,3939 … − 32,3939 … = 3239 − 32 = 3207;
99X = 3207;
X = 3207/99 = 1069/33.
Приступаем к третьей дроби: X = 0,30(5) = 0,30555 … Схема та же самая, поэтому я просто приведу выкладки:
Период k = 1 ⇒ умножаем все на 10k = 101 = 10;
10X = 10 · 0,30555 … = 3,05555 …
10X − X = 3,0555 … − 0,305555 … = 2,75 = 11/4;
9X = 11/4;
X = (11/4) : 9 = 11/36.
Наконец, последняя дробь: X = 0,(2475) = 0,2475 2475 … Опять же, для удобства периодические части отделены друг от друга пробелами. Имеем:
k = 4 ⇒ 10k = 104 = 10 000;
10 000X = 10 000 · 0,2475 2475 = 2475,2475 …
10 000X − X = 2475,2475 … − 0,2475 2475 … = 2475;
9999X = 2475;
X = 2475 : 9999 = 25/101.
Смотрите также:
- Сравнение дробей
- Тест к уроку «Десятичные дроби» (2 вариант)
- Четырехугольная пирамида в задаче C2
- Как сдать ЕГЭ по математике
- Задача B5: площадь сектора
- Задача B4: тарифы на сотовую связь

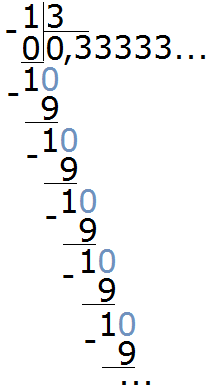
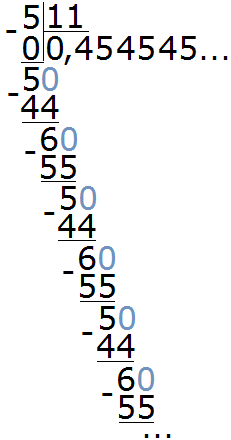
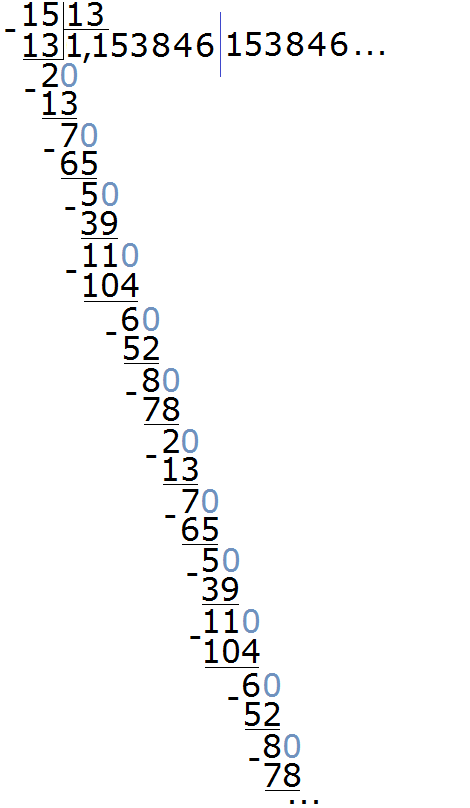
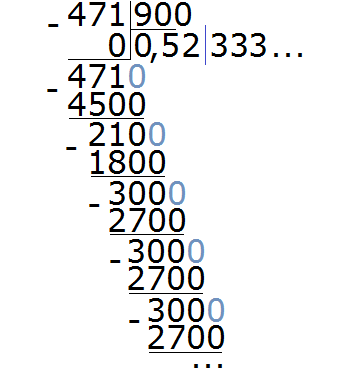

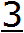
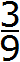
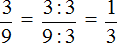
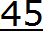
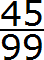
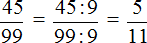
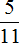
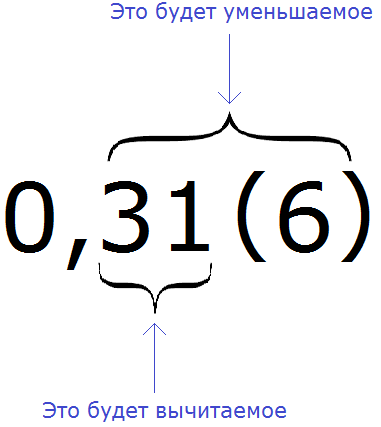
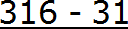
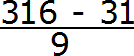
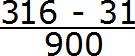
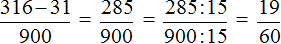
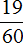
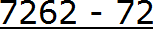
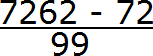
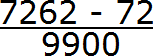
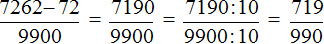
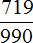

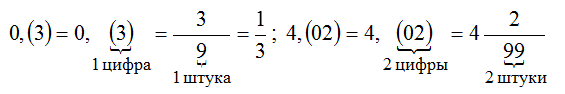

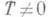 такое, что при любом
такое, что при любом 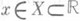 (или
(или  ) числа х-Т и x+Ттакже принадлежат множеству X и выполняется равенство
) числа х-Т и x+Ттакже принадлежат множеству X и выполняется равенство 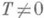 будет П.; для функции Дирихле
будет П.; для функции Дирихле  , имеет период
, имеет период 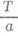 . Если действительная функция f(x). с действительным аргументом непрерывна на X(и не равна тождественно постоянной), то она имеет наименьший период T0>0 и всякий другой действительный П. кратен Т 0. Существуют функции с комплексным аргументом, у к-рых имеются два некратных с мнимым частным П.; таковы, напр., эллиптические функции.
. Если действительная функция f(x). с действительным аргументом непрерывна на X(и не равна тождественно постоянной), то она имеет наименьший период T0>0 и всякий другой действительный П. кратен Т 0. Существуют функции с комплексным аргументом, у к-рых имеются два некратных с мнимым частным П.; таковы, напр., эллиптические функции.