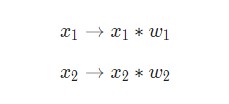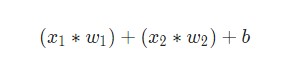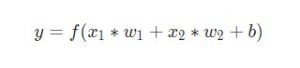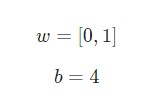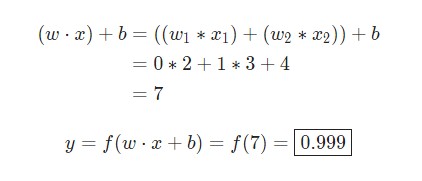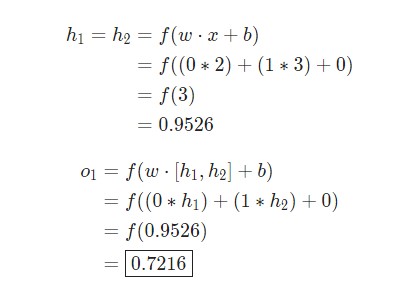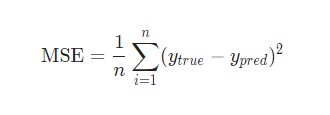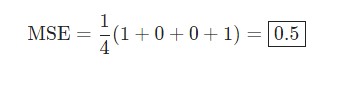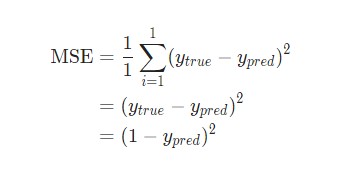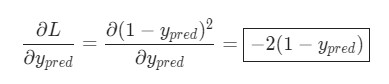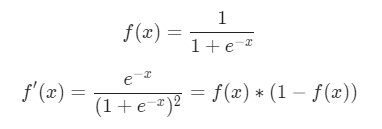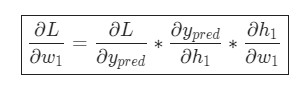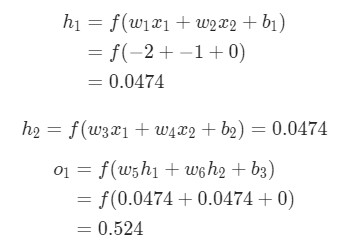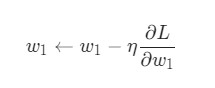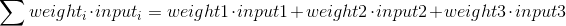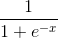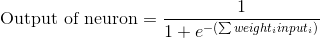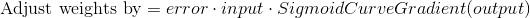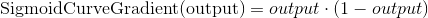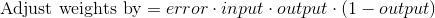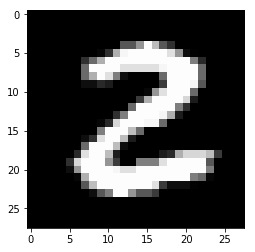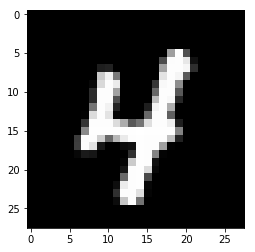Далее будет представлено максимально простое объяснение того, как работают нейронные сети, а также показаны способы их реализации в Python. Приятная новость для новичков – нейронные сети не такие уж и сложные. Термин нейронные сети зачастую используют в разговоре, ссылаясь на какой-то чрезвычайно запутанный концепт. На деле же все намного проще.
Данная статья предназначена для людей, которые ранее не работали с нейронными сетями вообще или же имеют довольно поверхностное понимание того, что это такое. Принцип работы нейронных сетей будет показан на примере их реализации через Python.
Содержание статьи
- Создание нейронных блоков
- Простой пример работы с нейронами в Python
- Создание нейрона с нуля в Python
- Пример сбор нейронов в нейросеть
- Пример прямого распространения FeedForward
- Создание нейронной сети прямое распространение FeedForward
- Пример тренировки нейронной сети — минимизация потерь, Часть 1
- Пример подсчета потерь в тренировки нейронной сети
- Python код среднеквадратической ошибки (MSE)
- Тренировка нейронной сети — многовариантные исчисления, Часть 2
- Пример подсчета частных производных
- Тренировка нейронной сети: Стохастический градиентный спуск
- Создание нейронной сети с нуля на Python
Создание нейронных блоков
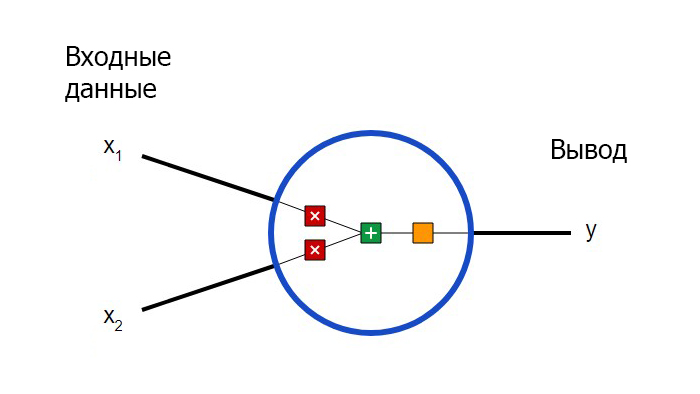
Для начала необходимо определиться с тем, что из себя представляют базовые компоненты нейронной сети – нейроны. Нейрон принимает вводные данные, выполняет с ними определенные математические операции, а затем выводит результат. Нейрон с двумя входными данными выглядит следующим образом:
Здесь происходят три вещи. Во-первых, каждый вход умножается на вес (на схеме обозначен красным):
Затем все взвешенные входы складываются вместе со смещением b (на схеме обозначен зеленым):
Наконец, сумма передается через функцию активации (на схеме обозначена желтым):
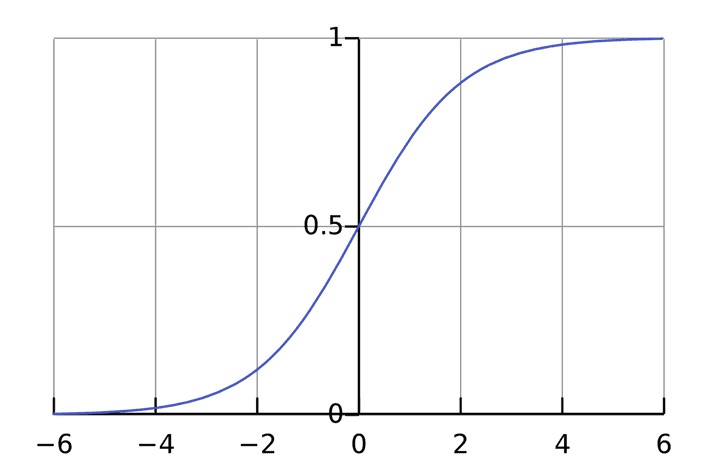
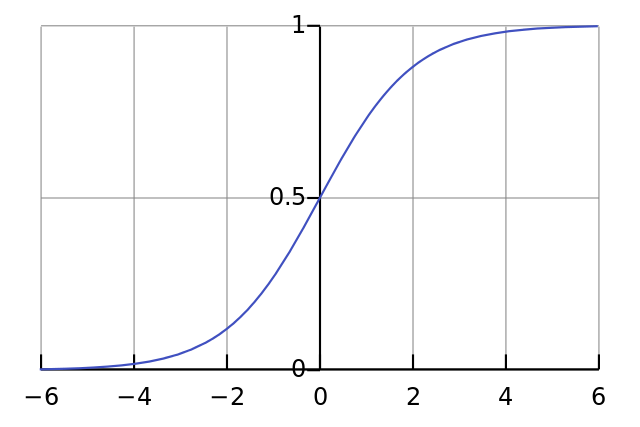
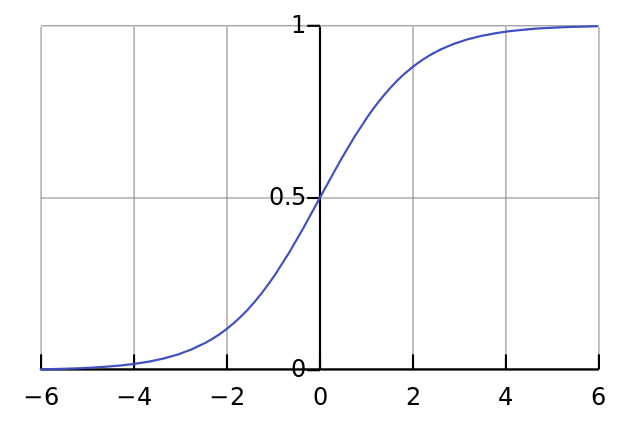
Функция активации используется для подключения несвязанных входных данных с выводом, у которого простая и предсказуемая форма. Как правило, в качестве используемой функцией активации берется функция сигмоида:
Функция сигмоида выводит только числа в диапазоне (0, 1). Вы можете воспринимать это как компрессию от (−∞, +∞) до (0, 1). Крупные отрицательные числа становятся ~0, а крупные положительные числа становятся ~1.
Предположим, у нас есть нейрон с двумя входами, который использует функцию активации сигмоида и имеет следующие параметры:
w = [0,1] — это просто один из способов написания w1 = 0, w2 = 1 в векторной форме. Присвоим нейрону вход со значением x = [2, 3]. Для более компактного представления будет использовано скалярное произведение.
С учетом, что вход был x = [2, 3], вывод будет равен 0.999. Вот и все. Такой процесс передачи входных данных для получения вывода называется прямым распространением, или feedforward.
Создание нейрона с нуля в Python
Есть вопросы по Python?
На нашем форуме вы можете задать любой вопрос и получить ответ от всего нашего сообщества!
Telegram Чат & Канал
Вступите в наш дружный чат по Python и начните общение с единомышленниками! Станьте частью большого сообщества!
Паблик VK
Одно из самых больших сообществ по Python в социальной сети ВК. Видео уроки и книги для вас!
Приступим к имплементации нейрона. Для этого потребуется использовать NumPy. Это мощная вычислительная библиотека Python, которая задействует математические операции:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
import numpy as np def sigmoid(x): # Наша функция активации: f(x) = 1 / (1 + e^(-x)) return 1 / (1 + np.exp(—x)) class Neuron: def __init__(self, weights, bias): self.weights = weights self.bias = bias def feedforward(self, inputs): # Вводные данные о весе, добавление смещения # и последующее использование функции активации total = np.dot(self.weights, inputs) + self.bias return sigmoid(total) weights = np.array([0, 1]) # w1 = 0, w2 = 1 bias = 4 # b = 4 n = Neuron(weights, bias) x = np.array([2, 3]) # x1 = 2, x2 = 3 print(n.feedforward(x)) # 0.9990889488055994 |
Узнаете числа? Это тот же пример, который рассматривался ранее. Ответ полученный на этот раз также равен 0.999.
Пример сбор нейронов в нейросеть
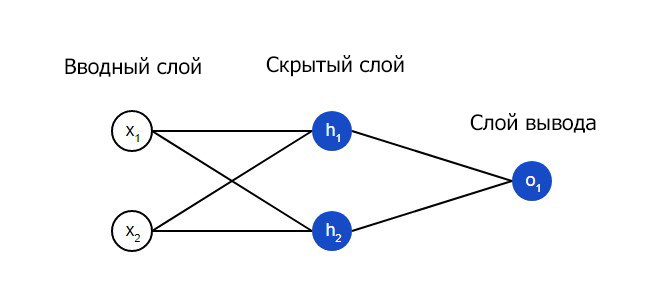
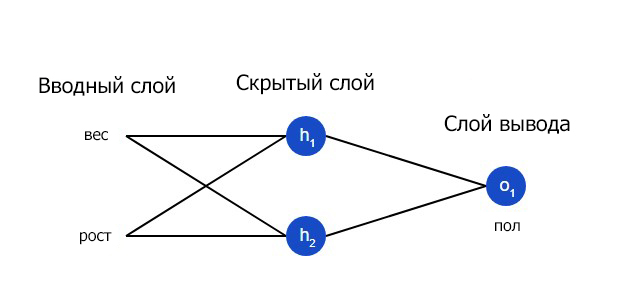
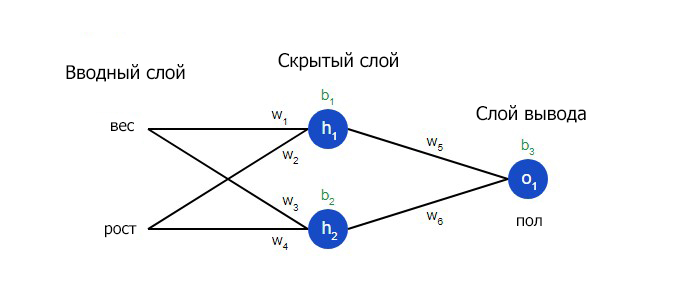
Нейронная сеть по сути представляет собой группу связанных между собой нейронов. Простая нейронная сеть выглядит следующим образом:
На вводном слое сети два входа – x1 и x2. На скрытом слое два нейтрона — h1 и h2. На слое вывода находится один нейрон – о1. Обратите внимание на то, что входные данные для о1 являются результатами вывода h1 и h2. Таким образом и строится нейросеть.
Скрытым слоем называется любой слой между вводным слоем и слоем вывода, что являются первым и последним слоями соответственно. Скрытых слоев может быть несколько.
Пример прямого распространения FeedForward
Давайте используем продемонстрированную выше сеть и представим, что все нейроны имеют одинаковый вес w = [0, 1], одинаковое смещение b = 0 и ту же самую функцию активации сигмоида. Пусть h1, h2 и o1 сами отметят результаты вывода представленных ими нейронов.
Что случится, если в качестве ввода будет использовано значение х = [2, 3]?
Результат вывода нейронной сети для входного значения х = [2, 3] составляет 0.7216. Все очень просто.
Нейронная сеть может иметь любое количество слоев с любым количеством нейронов в этих слоях.
Суть остается той же: нужно направить входные данные через нейроны в сеть для получения в итоге выходных данных. Для простоты далее в данной статье будет создан код сети, упомянутая выше.
Создание нейронной сети прямое распространение FeedForward
Далее будет показано, как реализовать прямое распространение feedforward в отношении нейронной сети. В качестве опорной точки будет использована следующая схема нейронной сети:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 |
import numpy as np # … Здесь код из предыдущего раздела class OurNeuralNetwork: «»» Нейронная сеть, у которой: — 2 входа — 1 скрытый слой с двумя нейронами (h1, h2) — слой вывода с одним нейроном (o1) У каждого нейрона одинаковые вес и смещение: — w = [0, 1] — b = 0 «»» def __init__(self): weights = np.array([0, 1]) bias = 0 # Класс Neuron из предыдущего раздела self.h1 = Neuron(weights, bias) self.h2 = Neuron(weights, bias) self.o1 = Neuron(weights, bias) def feedforward(self, x): out_h1 = self.h1.feedforward(x) out_h2 = self.h2.feedforward(x) # Вводы для о1 являются выводами h1 и h2 out_o1 = self.o1.feedforward(np.array([out_h1, out_h2])) return out_o1 network = OurNeuralNetwork() x = np.array([2, 3]) print(network.feedforward(x)) # 0.7216325609518421 |
Мы вновь получили 0.7216. Похоже, все работает.
Пример тренировки нейронной сети — минимизация потерь, Часть 1
Предположим, у нас есть следующие параметры:
| Имя/Name | Вес/Weight (фунты) | Рост/Height (дюймы) | Пол/Gender |
| Alice | 133 | 65 | F |
| Bob | 160 | 72 | M |
| Charlie | 152 | 70 | M |
| Diana | 120 | 60 | F |
Давайте натренируем нейронную сеть таким образом, чтобы она предсказывала пол заданного человека в зависимости от его веса и роста.
Мужчины Male будут представлены как 0, а женщины Female как 1. Для простоты представления данные также будут несколько смещены.
| Имя/Name | Вес/Weight (минус 135) | Рост/Height (минус 66) | Пол/Gender |
| Alice | -2 | -1 | 1 |
| Bob | 25 | 6 | 0 |
| Charlie | 17 | 4 | 0 |
| Diana | -15 | -6 | 1 |
Для оптимизации здесь произведены произвольные смещения
135и66. Однако, обычно для смещения выбираются средние показатели.
Потери
Перед тренировкой нейронной сети потребуется выбрать способ оценки того, насколько хорошо сеть справляется с задачами. Это необходимо для ее последующих попыток выполнять поставленную задачу лучше. Таков принцип потери.
В данном случае будет использоваться среднеквадратическая ошибка (MSE) потери:
Давайте разберемся:
n– число рассматриваемых объектов, которое в данном случае равно 4. ЭтоAlice,Bob,CharlieиDiana;y– переменные, которые будут предсказаны. В данном случае это пол человека;ytrue– истинное значение переменной, то есть так называемый правильный ответ. Например, дляAliceзначениеytrueбудет1, то естьFemale;ypred– предполагаемое значение переменной. Это результат вывода сети.
(ytrue - ypred)2 называют квадратичной ошибкой (MSE). Здесь функция потери просто берет среднее значение по всем квадратичным ошибкам. Отсюда и название ошибки. Чем лучше предсказания, тем ниже потери.
Лучшие предсказания = Меньшие потери.
Тренировка нейронной сети = стремление к минимизации ее потерь.
Пример подсчета потерь в тренировки нейронной сети
Скажем, наша сеть всегда выдает 0. Другими словами, она уверена, что все люди — Мужчины. Какой будет потеря?
| Имя/Name | ytrue | ypred | (ytrue — ypred)2 |
| Alice | 1 | 0 | 1 |
| Bob | 0 | 0 | 0 |
| Charlie | 0 | 0 | 0 |
| Diana | 1 | 0 | 1 |
Python код среднеквадратической ошибки (MSE)
Ниже представлен код для подсчета потерь:
|
import numpy as np def mse_loss(y_true, y_pred): # y_true и y_pred являются массивами numpy с одинаковой длиной return ((y_true — y_pred) ** 2).mean() y_true = np.array([1, 0, 0, 1]) y_pred = np.array([0, 0, 0, 0]) print(mse_loss(y_true, y_pred)) # 0.5 |
При возникновении сложностей с пониманием работы кода стоит ознакомиться с quickstart в NumPy для операций с массивами.
Тренировка нейронной сети — многовариантные исчисления, Часть 2
Текущая цель понятна – это минимизация потерь нейронной сети. Теперь стало ясно, что повлиять на предсказания сети можно при помощи изменения ее веса и смещения. Однако, как минимизировать потери?
В этом разделе будут затронуты многовариантные исчисления. Если вы не знакомы с данной темой, фрагменты с математическими вычислениями можно пропускать.
Для простоты давайте представим, что в наборе данных рассматривается только Alice:
| Имя/Name | Вес/Weight (минус 135) | Рост/Height (минус 66) | Пол/Gender |
| Alice | -2 | -1 | 1 |
Затем потеря среднеквадратической ошибки будет просто квадратической ошибкой для Alice:
Еще один способ понимания потери – представление ее как функции веса и смещения. Давайте обозначим каждый вес и смещение в рассматриваемой сети:
Затем можно прописать потерю как многовариантную функцию:
Представим, что нам нужно немного отредактировать w1. В таком случае, как изменится потеря L после внесения поправок в w1?
На этот вопрос может ответить частная производная . Как же ее вычислить?
Здесь математические вычисления будут намного сложнее. С первой попытки вникнуть будет непросто, но отчаиваться не стоит. Возьмите блокнот и ручку – лучше делать заметки, они помогут в будущем.
Для начала, давайте перепишем частную производную в контексте :
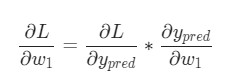
Подсчитать можно благодаря вычисленной выше
L = (1 - ypred)2:
Теперь, давайте определим, что делать с . Как и ранее, позволим
h1, h2, o1 стать результатами вывода нейронов, которые они представляют. Дальнейшие вычисления:
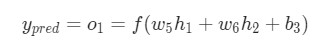
f является функцией активации сигмоида.
Так как w1 влияет только на h1, а не на h2, можно записать:
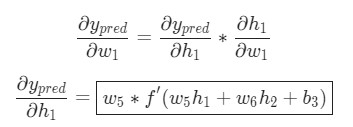
Те же самые действия проводятся для :
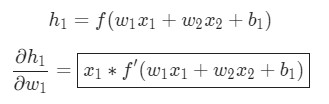
В данном случае х1 — вес, а х2 — рост. Здесь f′(x) как производная функции сигмоида встречается во второй раз. Попробуем вывести ее:
Функция f'(x) в таком виде будет использована несколько позже.
Вот и все. Теперь разбита на несколько частей, которые будут оптимальны для подсчета:
Эта система подсчета частных производных при работе в обратном порядке известна, как метод обратного распространения ошибки, или backprop.
У нас накопилось довольно много формул, в которых легко запутаться. Для лучшего понимания принципа их работы рассмотрим следующий пример.
Пример подсчета частных производных
В данном примере также будет задействована только Alice:
| Имя/Name | Вес/Weight (минус 135) | Рост/Height (минус 66) | Пол/Gender |
| Alice | -2 | -1 | 1 |
Здесь вес будет представлен как 1, а смещение как 0. Если выполним прямое распространение (feedforward) через сеть, получим:
Выдачи нейронной сети ypred = 0.524. Это дает нам слабое представление о том, рассматривается мужчина Male (0), или женщина Female (1). Давайте подсчитаем :
Напоминание: мы вывели
f '(x) = f (x) * (1 - f (x))ранее для нашей функции активации сигмоида.
У нас получилось! Результат говорит о том, что если мы собираемся увеличить w1, L немного увеличивается в результате.
Тренировка нейронной сети: Стохастический градиентный спуск
У нас есть все необходимые инструменты для тренировки нейронной сети. Мы используем алгоритм оптимизации под названием стохастический градиентный спуск (SGD), который говорит нам, как именно поменять вес и смещения для минимизации потерь. По сути, это отражается в следующем уравнении:
η является константой под названием оценка обучения, что контролирует скорость обучения. Все что мы делаем, так это вычитаем из
w1:
Если мы применим это на каждый вес и смещение в сети, потеря будет постепенно снижаться, а показатели сети сильно улучшатся.
Наш процесс тренировки будет выглядеть следующим образом:
- Выбираем один пункт из нашего набора данных. Это то, что делает его стохастическим градиентным спуском. Мы обрабатываем только один пункт за раз;
- Подсчитываем все частные производные потери по весу или смещению. Это может быть
,
и так далее;
- Используем уравнение обновления для обновления каждого веса и смещения;
- Возвращаемся к первому пункту.
Давайте посмотрим, как это работает на практике.
Создание нейронной сети с нуля на Python
Наконец, мы реализуем готовую нейронную сеть:
| Имя/Name | Вес/Weight (минус 135) | Рост/Height (минус 66) | Пол/Gender |
| Alice | -2 | -1 | 1 |
| Bob | 25 | 6 | 0 |
| Charlie | 17 | 4 | 0 |
| Diana | -15 | -6 | 1 |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 |
import numpy as np def sigmoid(x): # Функция активации sigmoid:: f(x) = 1 / (1 + e^(-x)) return 1 / (1 + np.exp(—x)) def deriv_sigmoid(x): # Производная от sigmoid: f'(x) = f(x) * (1 — f(x)) fx = sigmoid(x) return fx * (1 — fx) def mse_loss(y_true, y_pred): # y_true и y_pred являются массивами numpy с одинаковой длиной return ((y_true — y_pred) ** 2).mean() class OurNeuralNetwork: «»» Нейронная сеть, у которой: — 2 входа — скрытый слой с двумя нейронами (h1, h2) — слой вывода с одним нейроном (o1) *** ВАЖНО ***: Код ниже написан как простой, образовательный. НЕ оптимальный. Настоящий код нейронной сети выглядит не так. НЕ ИСПОЛЬЗУЙТЕ этот код. Вместо этого, прочитайте/запустите его, чтобы понять, как работает эта сеть. «»» def __init__(self): # Вес self.w1 = np.random.normal() self.w2 = np.random.normal() self.w3 = np.random.normal() self.w4 = np.random.normal() self.w5 = np.random.normal() self.w6 = np.random.normal() # Смещения self.b1 = np.random.normal() self.b2 = np.random.normal() self.b3 = np.random.normal() def feedforward(self, x): # x является массивом numpy с двумя элементами h1 = sigmoid(self.w1 * x[0] + self.w2 * x[1] + self.b1) h2 = sigmoid(self.w3 * x[0] + self.w4 * x[1] + self.b2) o1 = sigmoid(self.w5 * h1 + self.w6 * h2 + self.b3) return o1 def train(self, data, all_y_trues): «»» — data is a (n x 2) numpy array, n = # of samples in the dataset. — all_y_trues is a numpy array with n elements. Elements in all_y_trues correspond to those in data. «»» learn_rate = 0.1 epochs = 1000 # количество циклов во всём наборе данных for epoch in range(epochs): for x, y_true in zip(data, all_y_trues): # — Выполняем обратную связь (нам понадобятся эти значения в дальнейшем) sum_h1 = self.w1 * x[0] + self.w2 * x[1] + self.b1 h1 = sigmoid(sum_h1) sum_h2 = self.w3 * x[0] + self.w4 * x[1] + self.b2 h2 = sigmoid(sum_h2) sum_o1 = self.w5 * h1 + self.w6 * h2 + self.b3 o1 = sigmoid(sum_o1) y_pred = o1 # — Подсчет частных производных # — Наименование: d_L_d_w1 представляет «частично L / частично w1» d_L_d_ypred = —2 * (y_true — y_pred) # Нейрон o1 d_ypred_d_w5 = h1 * deriv_sigmoid(sum_o1) d_ypred_d_w6 = h2 * deriv_sigmoid(sum_o1) d_ypred_d_b3 = deriv_sigmoid(sum_o1) d_ypred_d_h1 = self.w5 * deriv_sigmoid(sum_o1) d_ypred_d_h2 = self.w6 * deriv_sigmoid(sum_o1) # Нейрон h1 d_h1_d_w1 = x[0] * deriv_sigmoid(sum_h1) d_h1_d_w2 = x[1] * deriv_sigmoid(sum_h1) d_h1_d_b1 = deriv_sigmoid(sum_h1) # Нейрон h2 d_h2_d_w3 = x[0] * deriv_sigmoid(sum_h2) d_h2_d_w4 = x[1] * deriv_sigmoid(sum_h2) d_h2_d_b2 = deriv_sigmoid(sum_h2) # — Обновляем вес и смещения # Нейрон h1 self.w1 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_w1 self.w2 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_w2 self.b1 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_b1 # Нейрон h2 self.w3 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_w3 self.w4 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_w4 self.b2 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_b2 # Нейрон o1 self.w5 -= learn_rate * d_L_d_ypred * d_ypred_d_w5 self.w6 -= learn_rate * d_L_d_ypred * d_ypred_d_w6 self.b3 -= learn_rate * d_L_d_ypred * d_ypred_d_b3 # — Подсчитываем общую потерю в конце каждой фазы if epoch % 10 == 0: y_preds = np.apply_along_axis(self.feedforward, 1, data) loss = mse_loss(all_y_trues, y_preds) print(«Epoch %d loss: %.3f» % (epoch, loss)) # Определение набора данных data = np.array([ [—2, —1], # Alice [25, 6], # Bob [17, 4], # Charlie [—15, —6], # Diana ]) all_y_trues = np.array([ 1, # Alice 0, # Bob 0, # Charlie 1, # Diana ]) # Тренируем нашу нейронную сеть! network = OurNeuralNetwork() network.train(data, all_y_trues) |
Вы можете поэкспериментировать с этим кодом самостоятельно. Он также доступен на Github.
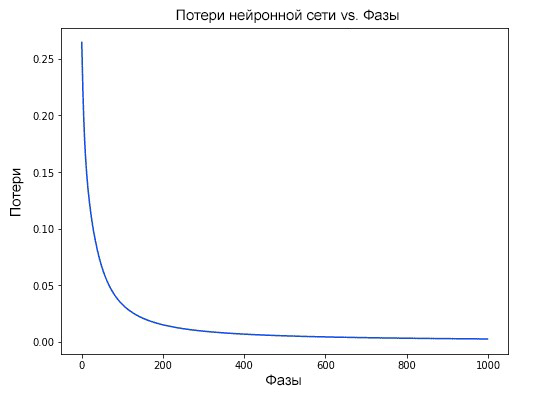
Наши потери постоянно уменьшаются по мере того, как учится нейронная сеть:
Теперь мы можем использовать нейронную сеть для предсказания полов:
|
# Делаем предсказания emily = np.array([—7, —3]) # 128 фунтов, 63 дюйма frank = np.array([20, 2]) # 155 фунтов, 68 дюймов print(«Emily: %.3f» % network.feedforward(emily)) # 0.951 — F print(«Frank: %.3f» % network.feedforward(frank)) # 0.039 — M |
Что теперь?
У вас все получилось. Вспомним, как мы это делали:
- Узнали, что такое нейроны, как создать блоки нейронных сетей;
- Использовали функцию активации сигмоида в отношении нейронов;
- Увидели, что по сути нейронные сети — это просто набор нейронов, связанных между собой;
- Создали набор данных с параметрами вес и рост в качестве входных данных (или функций), а также использовали пол в качестве вывода (или маркера);
- Узнали о функциях потерь и среднеквадратичной ошибке (MSE);
- Узнали, что тренировка нейронной сети — это минимизация ее потерь;
- Использовали обратное распространение для вычисления частных производных;
- Использовали стохастический градиентный спуск (SGD) для тренировки нейронной сети.
Подробнее о построении нейронной сети прямого распросранения Feedforward можно ознакомиться в одной из предыдущих публикаций.
Спасибо за внимание!
Являюсь администратором нескольких порталов по обучению языков программирования Python, Golang и Kotlin. В составе небольшой команды единомышленников, мы занимаемся популяризацией языков программирования на русскоязычную аудиторию. Большая часть статей была адаптирована нами на русский язык и распространяется бесплатно.
E-mail: vasile.buldumac@ati.utm.md
Образование
Universitatea Tehnică a Moldovei (utm.md)
- 2014 — 2018 Технический Университет Молдовы, ИТ-Инженер. Тема дипломной работы «Автоматизация покупки и продажи криптовалюты используя технический анализ»
- 2018 — 2020 Технический Университет Молдовы, Магистр, Магистерская диссертация «Идентификация человека в киберпространстве по фотографии лица»
Время на прочтение
8 мин
Количество просмотров 502K
О чём статья
Лично я лучше всего обучаюсь при помощи небольшого работающего кода, с которым могу поиграться. В этом пособии мы научимся алгоритму обратного распространения ошибок на примере небольшой нейронной сети, реализованной на Python.
Дайте код!
X = np.array([ [0,0,1],[0,1,1],[1,0,1],[1,1,1] ])
y = np.array([[0,1,1,0]]).T
syn0 = 2*np.random.random((3,4)) - 1
syn1 = 2*np.random.random((4,1)) - 1
for j in xrange(60000):
l1 = 1/(1+np.exp(-(np.dot(X,syn0))))
l2 = 1/(1+np.exp(-(np.dot(l1,syn1))))
l2_delta = (y - l2)*(l2*(1-l2))
l1_delta = l2_delta.dot(syn1.T) * (l1 * (1-l1))
syn1 += l1.T.dot(l2_delta)
syn0 += X.T.dot(l1_delta)
Слишком сжато? Давайте разобьём его на более простые части.
Часть 1: Небольшая игрушечная нейросеть
Нейросеть, тренируемая через обратное распространение (backpropagation), пытается использовать входные данные для предсказания выходных.
Вход Выход
0 0 1 0
1 1 1 1
1 0 1 1
0 1 1 0
Предположим, нам нужно предсказать, как будет выглядеть колонка «выход» на основе входных данных. Эту задачу можно было бы решить, подсчитав статистическое соответствие между ними. И мы бы увидели, что с выходными данными на 100% коррелирует левый столбец.
Обратное распространение, в самом простом случае, рассчитывает подобную статистику для создания модели. Давайте попробуем.
Нейросеть в два слоя
import numpy as np
# Сигмоида
def nonlin(x,deriv=False):
if(deriv==True):
return f(x)*(1-f(x))
return 1/(1+np.exp(-x))
# набор входных данных
X = np.array([ [0,0,1],
[0,1,1],
[1,0,1],
[1,1,1] ])
# выходные данные
y = np.array([[0,0,1,1]]).T
# сделаем случайные числа более определёнными
np.random.seed(1)
# инициализируем веса случайным образом со средним 0
syn0 = 2*np.random.random((3,1)) - 1
for iter in xrange(10000):
# прямое распространение
l0 = X
l1 = nonlin(np.dot(l0,syn0))
# насколько мы ошиблись?
l1_error = y - l1
# перемножим это с наклоном сигмоиды
# на основе значений в l1
l1_delta = l1_error * nonlin(l1,True) # !!!
# обновим веса
syn0 += np.dot(l0.T,l1_delta) # !!!
print "Выходные данные после тренировки:"
print l1
Выходные данные после тренировки:
[[ 0.00966449]
[ 0.00786506]
[ 0.99358898]
[ 0.99211957]]
Переменные и их описания.
X — матрица входного набор данных; строки – тренировочные примеры
y – матрица выходного набора данных; строки – тренировочные примеры
l0 – первый слой сети, определённый входными данными
l1 – второй слой сети, или скрытый слой
syn0 – первый слой весов, Synapse 0, объединяет l0 с l1.
«*» — поэлементное умножение – два вектора одного размера умножают соответствующие значения, и на выходе получается вектор такого же размера
«-» – поэлементное вычитание векторов
x.dot(y) – если x и y – это вектора, то на выходе получится скалярное произведение. Если это матрицы, то получится перемножение матриц. Если матрица только одна из них – это перемножение вектора и матрицы.
И это работает! Рекомендую перед прочтением объяснения поиграться немного с кодом и понять, как он работает. Он должен запускаться прямо как есть, в ipython notebook. С чем можно повозиться в коде:
- сравните l1 после первой итерации и после последней
- посмотрите на функцию nonlin.
- посмотрите, как меняется l1_error
- разберите строку 36 – основные секретные ингредиенты собраны тут (отмечена !!!)
- разберите строку 39 – вся сеть готовится именно к этой операции (отмечена !!!)
Разберём код по строчкам
import numpy as np
Импортирует numpy, библиотеку линейной алгебры. Единственная наша зависимость.
def nonlin(x,deriv=False):
Наша нелинейность. Конкретно эта функция создаёт «сигмоиду». Она ставит в соответствие любое число значению от 0 до 1 и преобразовывает числа в вероятности, а также имеет несколько других полезных для тренировки нейросетей свойств.
if(deriv==True):
Эта функция также умеет выдавать производную сигмоиды (deriv=True). Это одно из её полезных свойств. Если выход функции – это переменная out, тогда производная будет out * (1-out). Эффективно.
X = np.array([ [0,0,1], …
Инициализация массива входных данных в виде numpy-матрицы. Каждая строка – тренировочный пример. Столбцы – это входные узлы. У нас получается 3 входных узла в сети и 4 тренировочных примера.
y = np.array([[0,0,1,1]]).T
Инициализирует выходные данные. «.T» – функция переноса. После переноса у матрицы y есть 4 строки с одним столбцом. Как и в случае входных данных, каждая строка – это тренировочный пример, и каждый столбец (в нашем случае один) – выходной узел. У сети, получается, 3 входа и 1 выход.
np.random.seed(1)
Благодаря этому случайное распределение будет каждый раз одним и тем же. Это позволит нам проще отслеживать работу сети после внесения изменений в код.
syn0 = 2*np.random.random((3,1)) – 1
Матрица весов сети. syn0 означает «synapse zero». Так как у нас всего два слоя, вход и выход, нам нужна одна матрица весов, которая их свяжет. Её размерность (3, 1), поскольку у нас есть 3 входа и 1 выход. Иными словами, l0 имеет размер 3, а l1 – 1. Поскольку мы связываем все узлы в l0 со всеми узлами l1, нам требуется матрица размерности (3, 1).
Заметьте, что она инициализируется случайным образом, и среднее значение равно нулю. За этим стоит достаточно сложная теория. Пока просто примем это как рекомендацию. Также заметим, что наша нейросеть – это и есть эта самая матрица. У нас есть «слои» l0 и l1, но они представляют собой временные значения, основанные на наборе данных. Мы их не храним. Всё обучение хранится в syn0.
for iter in xrange(10000):
Тут начинается основной код тренировки сети. Цикл с кодом повторяется многократно и оптимизирует сеть для набора данных.
l0 = X
Первый слой, l0, это просто данные. В X содержится 4 тренировочных примера. Мы обработаем их все и сразу – это называется групповой тренировкой [full batch]. Итого мы имеем 4 разных строки l0, но их можно представить себе как один тренировочный пример – на этом этапе это не имеет значения (можно было загрузить их 1000 или 10000 без всяких изменений в коде).
l1 = nonlin(np.dot(l0,syn0))
Это шаг предсказания. Мы позволяем сети попробовать предсказать вывод на основе ввода. Затем мы посмотрим, как это у неё получается, чтобы можно было подправить её в сторону улучшения.
В строке содержится два шага. Первый делает матричное перемножение l0 и syn0. Второй передаёт вывод через сигмоиду. Размерности у них следующие:
(4 x 3) dot (3 x 1) = (4 x 1)
Матричные умножения требуют, чтобы в середине уравнения размерности совпадали. Итоговая матрица имеет количество строк, как у первой, а столбцов – как у второй.
Мы загрузили 4 тренировочных примера, и получили 4 догадки (матрица 4х1). Каждый вывод соответствует догадке сети для данного ввода.
l1_error = y - l1
Поскольку в l1 содержатся догадки, мы можем сравнить их разницу с реальностью, вычитая её l1 из правильного ответа y. l1_error – вектор из положительных и отрицательных чисел, характеризующий «промах» сети.
l1_delta = l1_error * nonlin(l1,True)
А вот и секретный ингредиент. Эту строку нужно разбирать по частям.
Первая часть: производная
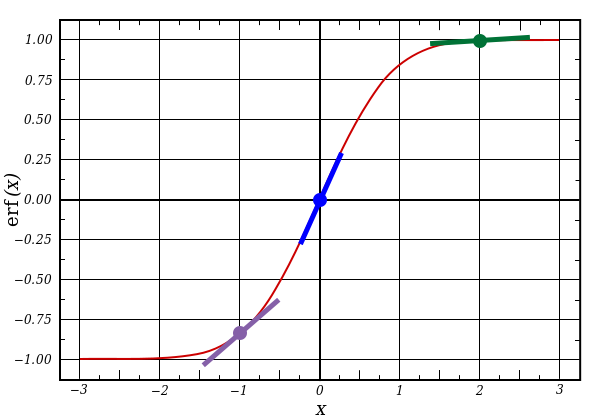
nonlin(l1,True)
l1 представляет три этих точки, а код выдаёт наклон линий, показанных ниже. Заметьте, что при больших значениях вроде x=2.0 (зелёная точка) и очень малые, вроде x=-1.0 (фиолетовая) линии имеют небольшой уклон. Самый большой угол у точки х=0 (голубая). Это имеет большое значение. Также отметьте, что все производные лежат в пределах от 0 до 1.
Полное выражение: производная, взвешенная по ошибкам
l1_delta = l1_error * nonlin(l1,True)
Математически существуют более точные способы, но в нашем случае подходит и этот. l1_error – это матрица (4,1). nonlin(l1,True) возвращает матрицу (4,1). Здесь мы поэлементно их перемножаем, и на выходе тоже получаем матрицу (4,1), l1_delta.
Умножая производные на ошибки, мы уменьшаем ошибки предсказаний, сделанных с высокой уверенностью. Если наклон линии был небольшим, то в сети содержится либо очень большое, либо очень малое значение. Если догадка в сети близка к нулю (х=0, у=0,5), то она не особенно уверенная. Мы обновляем эти неуверенные предсказания и оставляем в покое предсказания с высокой уверенностью, умножая их на величины, близкие к нулю.
syn0 += np.dot(l0.T,l1_delta)
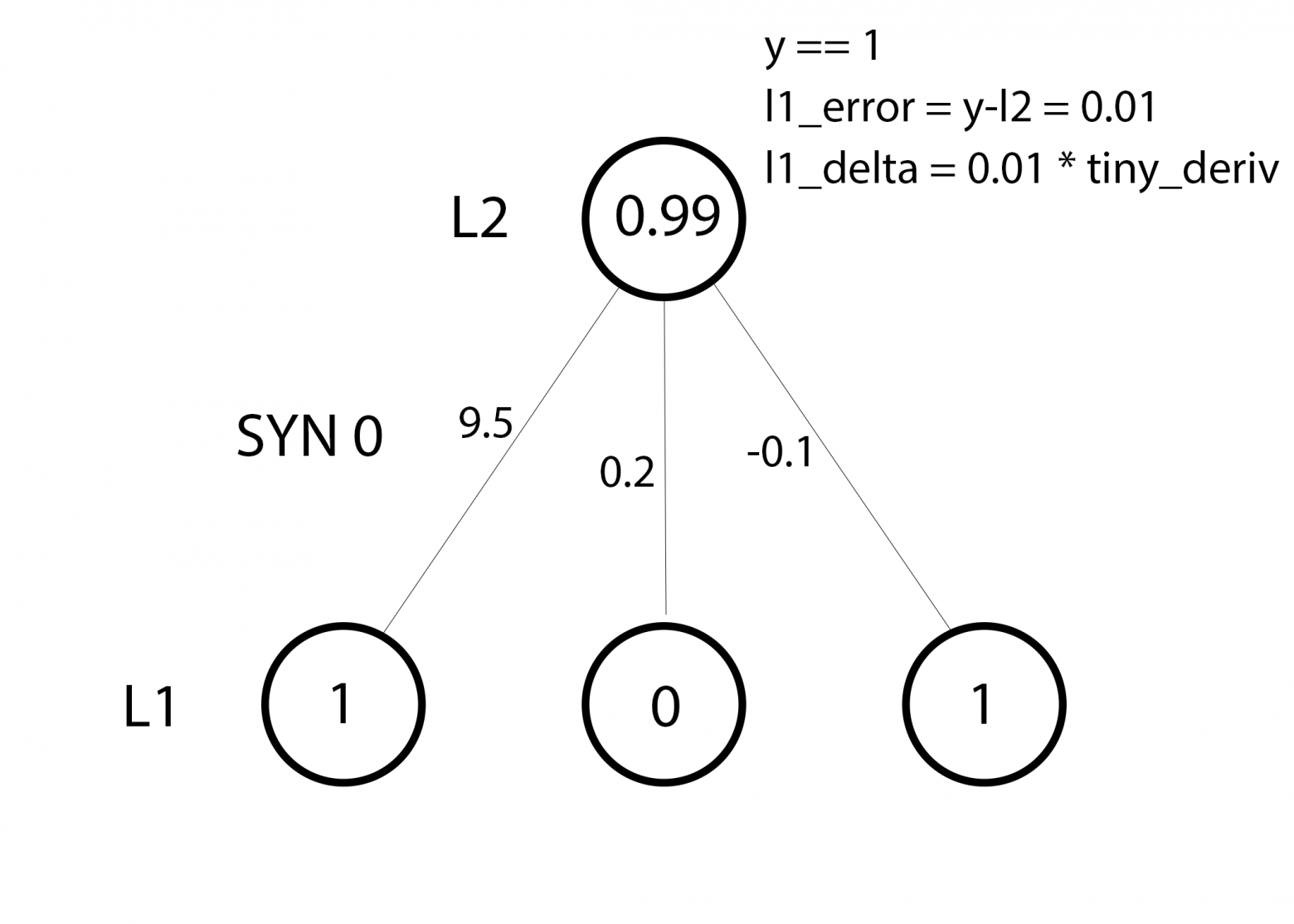
Мы готовы к обновлению сети. Рассмотрим один тренировочный пример. В нём мы будем обновлять веса. Обновим крайний левый вес (9.5)
weight_update = input_value * l1_delta
Для крайнего левого веса это будет 1.0 * l1_delta. Предположительно, это лишь незначительно увеличит 9.5. Почему? Поскольку предсказание было уже достаточно уверенным, и предсказания были практически правильными. Небольшая ошибка и небольшой наклон линии означает очень небольшое обновление.
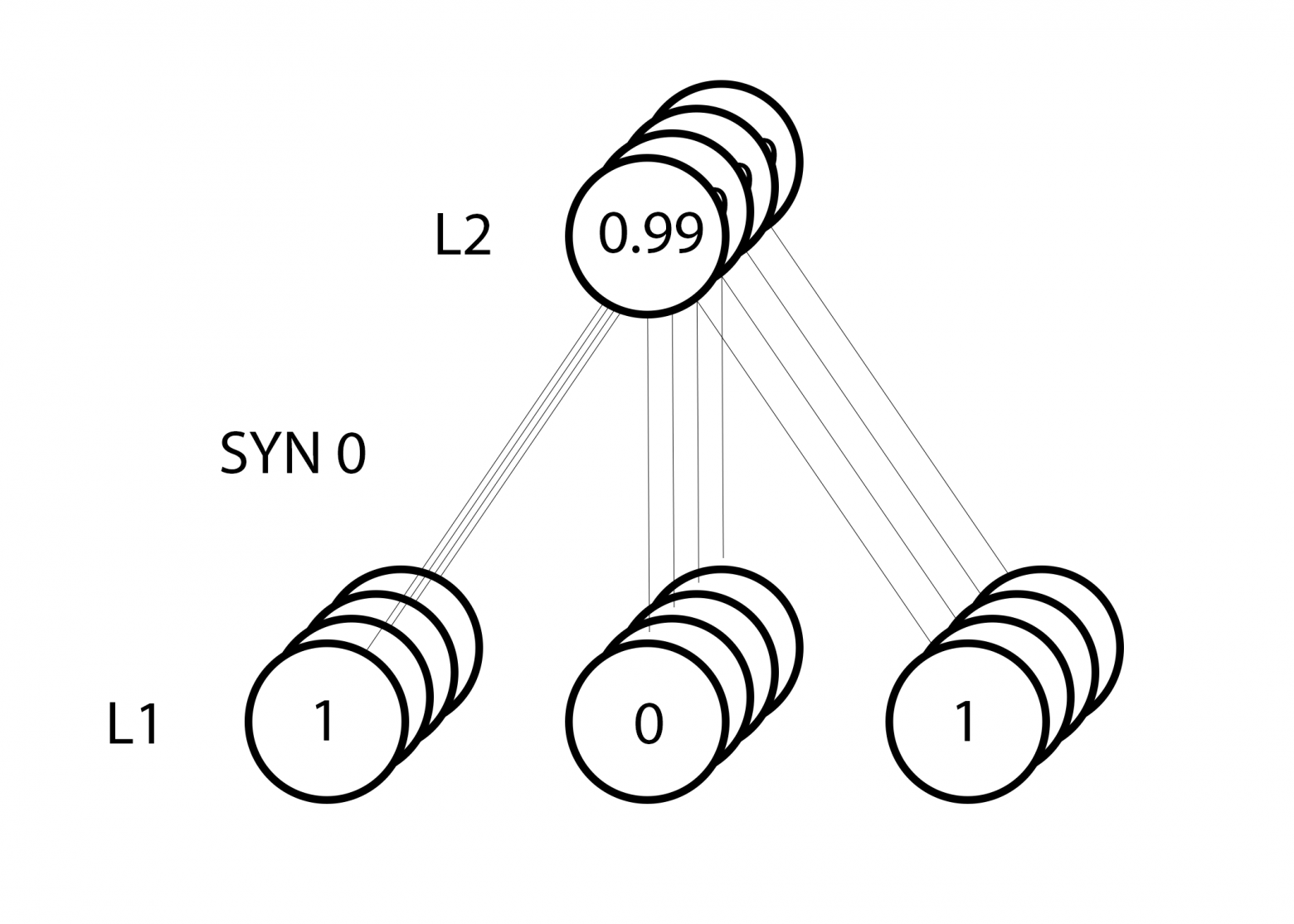
Но поскольку мы делаем групповую тренировку, указанный выше шаг мы повторяем для всех четырёх тренировочных примеров. Так что это выглядит очень похоже на изображение вверху. Так что же делает наша строчка? Она подсчитывает обновления весов для каждого веса, для каждого тренировочного примера, суммирует их и обновляет все веса – и всё одной строкой.
Понаблюдав за обновлением сети, вернёмся к нашим тренировочным данным. Когда и вход, и выход равны 1, мы увеличиваем вес между ними. Когда вход 1, а выход – 0, мы уменьшаем вес.
Вход Выход
0 0 1 0
1 1 1 1
1 0 1 1
0 1 1 0
Таким образом, в наших четырёх тренировочных примерах ниже, вес первого входа по отношению к выходу будет постоянно увеличиваться или оставаться постоянным, а два других веса будут увеличиваться и уменьшаться в зависимости от примеров. Этот эффект и способствует обучению сети на основе корреляций входных и выходных данных.
Часть 2: задачка посложнее
Вход Выход
0 0 1 0
0 1 1 1
1 0 1 1
1 1 1 0
Попробуем предсказать выходные данные на основе трёх входных столбцов данных. Ни один из входных столбцов не коррелирует на 100% с выходным. Третий столбец вообще ни с чем не связан, поскольку в нём всю дорогу содержатся единицы. Однако и тут можно увидеть схему – если в одном из двух первых столбцов (но не в обоих сразу) содержится 1, то результат также будет равен 1.
Это нелинейная схема, поскольку прямого соответствия столбцов один к одному не существует. Соответствие строится на комбинации входных данных, столбцов 1 и 2.
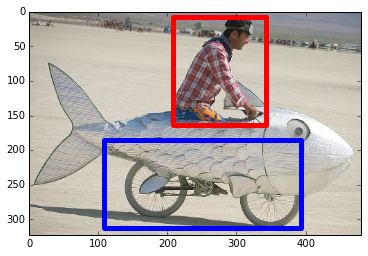
Интересно, что распознавание образов является очень похожей задачей. Если у вас есть 100 картинок одинакового размера, на которых изображены велосипеды и курительные трубки, присутствие на них определённых пикселей в определённых местах не коррелирует напрямую с наличием на изображении велосипеда или трубки. Статистически их цвет может казаться случайным. Но некоторые комбинации пикселей не случайны – те, что формируют изображение велосипеда (или трубки).
Стратегия
Чтобы скомбинировать пиксели в нечто, у чего может появиться однозначное соответствие с выходными данными, нужно добавить ещё один слой. Первый слой комбинирует вход, второй назначает соответствие выходу, используя в качестве входных данных выходные данные первого слоя. Обратите внимание на таблицу.
Вход (l0) Скрытые веса (l1) Выход (l2)
0 0 1 0.1 0.2 0.5 0.2 0
0 1 1 0.2 0.6 0.7 0.1 1
1 0 1 0.3 0.2 0.3 0.9 1
1 1 1 0.2 0.1 0.3 0.8 0
Случайным образом назначив веса, мы получим скрытые значения для слоя №1. Интересно, что у второго столбца скрытых весов уже есть небольшая корреляция с выходом. Не идеальная, но есть. И это тоже является важной частью процесса тренировки сети. Тренировка будет только усиливать эту корреляцию. Она будет обновлять syn1, чтобы назначить её соответствие выходным данным, и syn0, чтобы лучше получать данные со входа.
Нейросеть в три слоя
import numpy as np
def nonlin(x,deriv=False):
if(deriv==True):
return f(x)*(1-f(x))
return 1/(1+np.exp(-x))
X = np.array([[0,0,1],
[0,1,1],
[1,0,1],
[1,1,1]])
y = np.array([[0],
[1],
[1],
[0]])
np.random.seed(1)
# случайно инициализируем веса, в среднем - 0
syn0 = 2*np.random.random((3,4)) - 1
syn1 = 2*np.random.random((4,1)) - 1
for j in xrange(60000):
# проходим вперёд по слоям 0, 1 и 2
l0 = X
l1 = nonlin(np.dot(l0,syn0))
l2 = nonlin(np.dot(l1,syn1))
# как сильно мы ошиблись относительно нужной величины?
l2_error = y - l2
if (j% 10000) == 0:
print "Error:" + str(np.mean(np.abs(l2_error)))
# в какую сторону нужно двигаться?
# если мы были уверены в предсказании, то сильно менять его не надо
l2_delta = l2_error*nonlin(l2,deriv=True)
# как сильно значения l1 влияют на ошибки в l2?
l1_error = l2_delta.dot(syn1.T)
# в каком направлении нужно двигаться, чтобы прийти к l1?
# если мы были уверены в предсказании, то сильно менять его не надо
l1_delta = l1_error * nonlin(l1,deriv=True)
syn1 += l1.T.dot(l2_delta)
syn0 += l0.T.dot(l1_delta)
Error:0.496410031903
Error:0.00858452565325
Error:0.00578945986251
Error:0.00462917677677
Error:0.00395876528027
Error:0.00351012256786
Переменные и их описания
X — матрица входного набор данных; строки – тренировочные примеры
y – матрица выходного набора данных; строки – тренировочные примеры
l0 – первый слой сети, определённый входными данными
l1 – второй слой сети, или скрытый слой
l2 – финальный слой, это наша гипотеза. По мере тренировки должен приближаться к правильному ответу
syn0 – первый слой весов, Synapse 0, объединяет l0 с l1.
syn1 – второй слой весов, Synapse 1, объединяет l1 с l2.
l2_error – промах сети в количественном выражении
l2_delta – ошибка сети, в зависимости от уверенности предсказания. Почти совпадает с ошибкой, за исключением уверенных предсказаний
l1_error – взвешивая l2_delta весами из syn1, мы подсчитываем ошибку в среднем/скрытом слое
l1_delta – ошибки сети из l1, масштабируемые по увеернности предсказаний. Почти совпадает с l1_error, за исключением уверенных предсказаний
Код должен быть достаточно понятным – это просто предыдущая реализация сети, сложенная в два слоя один над другим. Выход первого слоя l1 – это вход второго слоя. Что-то новое есть лишь в следующей строке.
l1_error = l2_delta.dot(syn1.T)
Использует ошибки, взвешенные по уверенности предсказаний из l2, чтобы подсчитать ошибку для l1. Получаем, можно сказать, ошибку, взвешенную по вкладам – мы подсчитываем, какой вклад в ошибки в l2 вносят значения в узлах l1. Этот шаг и называется обратным распространением ошибок. Затем мы обновляем syn0, используя тот же алгоритм, что и в варианте с нейросетью из двух слоёв.
Сегодня мы разберём, зачем нужна библиотека TensorFlow и как её установить, что такое машинное обучение и как научить компьютер решать уравнения. Всё это — в одной статье.
Фреймворк TensorFlow — это относительно простой инструмент, который позволяет быстро создавать нейросети любой сложности. Он очень дружелюбен для начинающих, потому что содержит много примеров и уже готовых моделей машинного обучения, которые можно встроить в любое приложение. А продвинутым разработчикам TensorFlow предоставляет тонкие настройки и API для ускоренного обучения.
TensorFlow поддерживает несколько языков программирования. Главный из них — это Python. Кроме того, есть отдельные пакеты для C/C++, Golang и Java. А ещё — форк TensorFlow.js для исполнения кода на стороне клиента, в браузере, на JavaScript.
Этим возможности фреймворка TensorFlow не ограничиваются. Библиотеку также можно использовать для обучения моделей на смартфонах и умных устройствах (TensorFlow Lite) и создания корпоративных нейросетей (TensorFlow Extended).
Чтобы создать простую нейросеть на TensorFlow, достаточно понимать несколько основных принципов:
- что такое машинное обучение;
- как обучаются нейросети и какие методы для этого используются;
- как весь процесс обучения выглядит в TensorFlow.
О каждом из этих пунктов мы расскажем подробнее ниже.
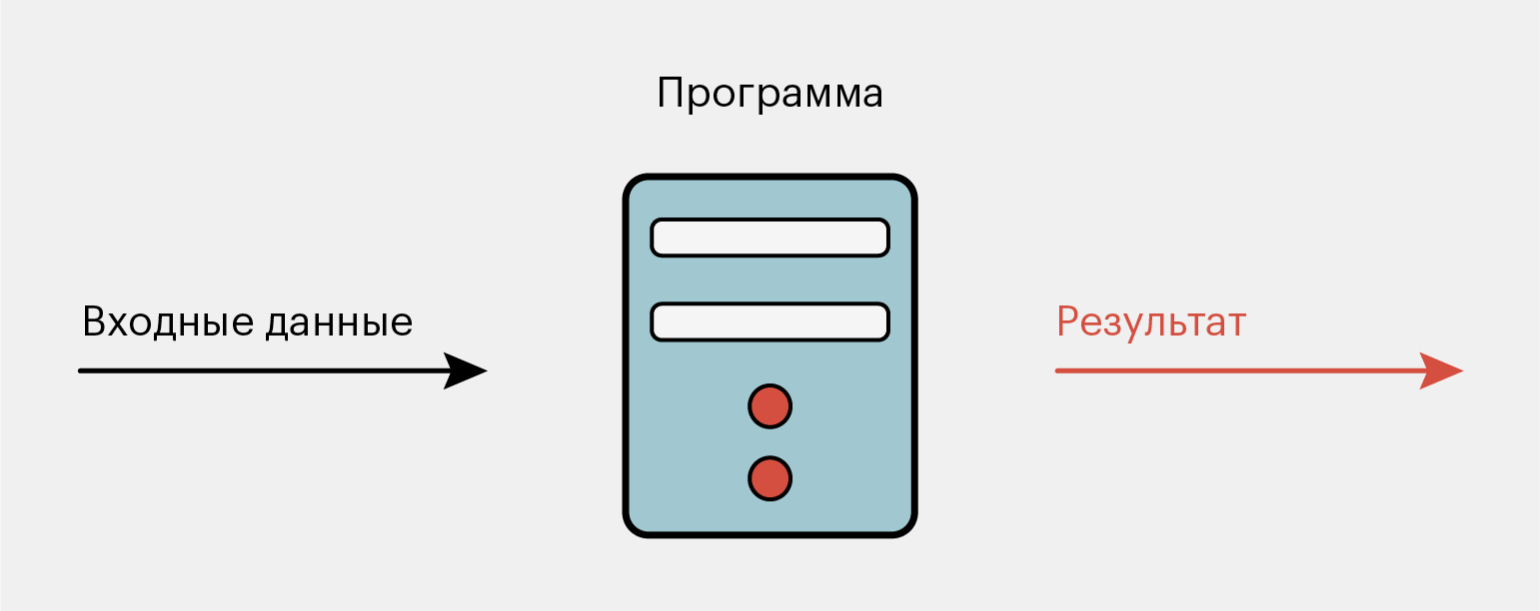
В обычном программировании всё работает по заранее заданным инструкциям. Разработчики их прописывают с помощью выражений, а компьютер строго им подчиняется. В конце выполнения компьютер выдаёт результат.
Например, если описать в обычной программе, как вычисляется площадь квадрата, компьютер будет строго следовать инструкции и всегда выдавать стабильный результат. Он не начнёт придумывать новые методы вычисления и не будет пытаться оптимизировать сам процесс вычисления. Он будет всегда следовать правилам — тому самому алгоритму, выраженному с помощью языка программирования.
Иллюстрация: Оля Ежак для Skillbox Media
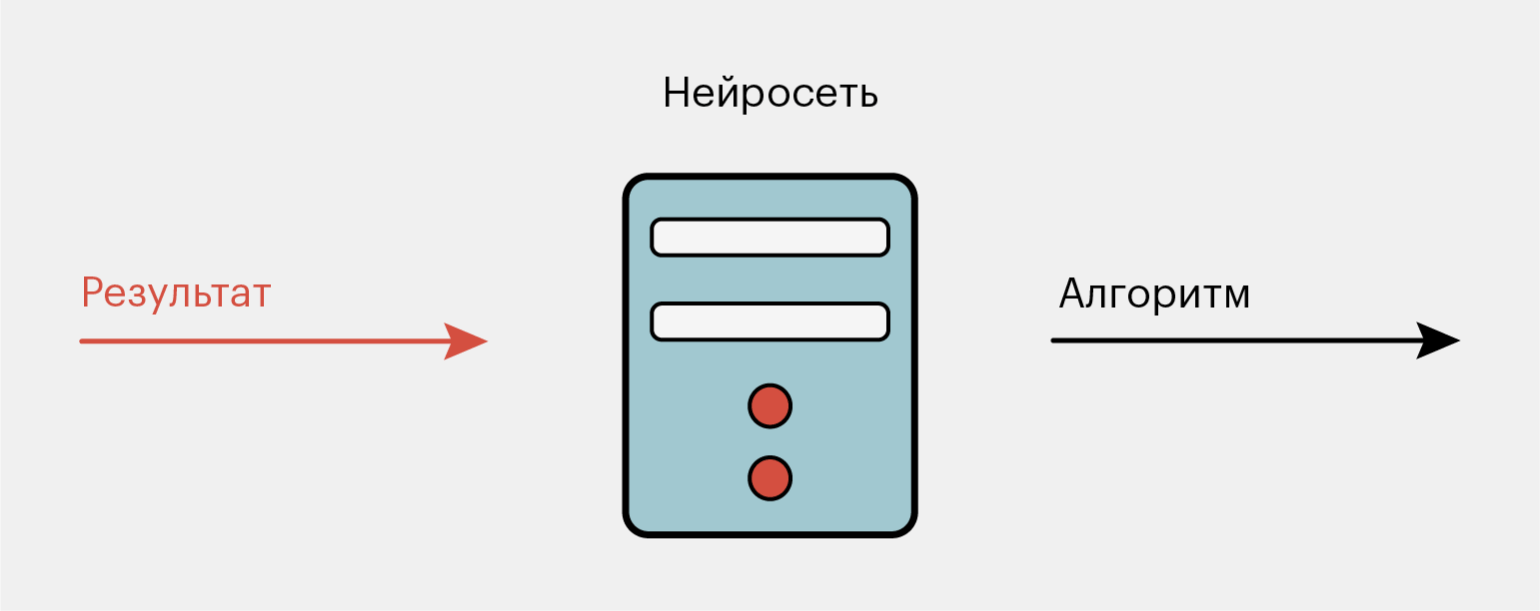
Машинное обучение работает по-другому. Нам нужно отдать компьютеру уже готовые результаты и входные данные и сказать: «Найди алгоритм, который сможет сделать из этих входных данных вот эти результаты». Нам неважно, как он будет это делать. Для нас важнее, чтобы результаты были точными.
Ещё мы должны говорить компьютеру, когда он ответил правильно, а когда — неправильно. Это сделает обучение эффективным и позволит нейросети постепенно двигаться в сторону более точных результатов.
Иллюстрация: Оля Ежак для Skillbox Media
В целом машинное обучение похоже на обучение обычного человека. Например, чтобы различать обувь и одежду, нам нужно посмотреть на какое-то количество экземпляров обуви и одежды, высказать свои предположения относительно того, что именно сейчас находится перед нами, получить обратную связь от кого-то, кто уже умеет их различать, — и тогда у нас появится алгоритм, как отличать одно от другого. Увидев туфли после успешного обучения, мы сразу сможем сказать, что это обувь, потому что по всем признакам они соответствуют этой категории.
Чтобы начать пользоваться фреймворком TensorFlow, можно выбрать один из вариантов:
- установить его на компьютер;
- воспользоваться облачным сервисом Google Colab.
В начале можно попробовать второй вариант, потому что для него не нужно ничего скачивать — всё хранится и работает в облаке. К тому же вычисления не нуждаются в мощностях вашего компьютера, вместо этого используются серверы Google.
Заходим на сайт Google Colab и создаём новый notebook:
Скриншот: Skillbox Media
У нас появится новое пространство, в котором мы и будем писать весь код. Сверху слева можно изменить название документа:
Скриншот: Skillbox Media
Google Colab состоит из ячеек с кодом или текстом. Чтобы создать ячейку с кодом, нужно нажать на кнопку + Code. Ниже появится ячейка, где можно писать Python‑код:
Скриншот: Skillbox Media
Теперь нам нужно проверить, что всё работает. Для этого попробуем экспортировать библиотеку в Google Colab. Делается это через команду import tensorflow as tf:
Скриншот: Skillbox Media
Всё готово. Рассмотрим второй способ, как можно подключить TensorFlow прямо на компьютере.
Чтобы использовать библиотеку TensorFlow на компьютере, её нужно установить через пакетный менеджер PIP.
Открываем терминал и вводим следующую команду:
pip install --upgrade pip
Мы обновили PIP до последней версии. Теперь скачиваем сам TensorFlow:
pip install tensorflow
Если всё прошло успешно, теперь вы можете подключать TensorFlow в Python-коде у вас на компьютере с помощью команды:
import tensorflow as tf
Но если возникли какие-то ошибки, можете прочитать более подробный гайд на официальном сайте TensorFlow и убедиться, что у вас скачаны все нужные пакеты.
Ниже мы будем использовать Google Colab для примеров, но код должен работать одинаково и корректно где угодно.
Допустим, у нас есть два набора чисел X и Y:
X: -1 0 1 2 3 4 Y: -4 1 6 11 16 21
Мы видим, что их значения связаны по какому-то правилу. Это правило: Y = 5X + 1. Но чтобы компьютер это понял, ему нужно научиться сопоставлять входные данные — X — с результатом — Y. У него сначала могут получаться странные уравнения типа: 2X — 5, 8X + 1, 4X + 2, 5X — 1. Но, обучившись немного, он найдёт наиболее близкую к исходной формулу.
Обучается нейросеть итеративно — или поэтапно. На каждой итерации она будет предлагать алгоритм, по которому входные значения сопоставляются с результатом. Затем она проверит свои предположения, вычислив все входные данные по формуле и сравнив с настоящими результатами. Так она узнает, насколько сильно ошиблась. И уже на основе этих ошибок скорректирует формулу на следующей итерации.
Количество итераций ограничено разве что временем разработчика. Главное — чтобы нейросеть на каждом шаге улучшала свои предположения, иначе весь процесс обучения будет бессмысленным.
Теперь давайте создадим модель, которая научится решать поставленную выше задачу. Сперва подключим необходимые зависимости:
import tensorflow as tf import numpy as np from tensorflow import keras
Первая зависимость — это наша библиотека TensorFlow, название которой мы сокращаем до tf, чтобы было удобнее её вызывать в программе. NumPy — это библиотека для эффективной работы с массивами чисел. Можно было, конечно, использовать и обычные списки, но NumPy будет работать намного быстрее, поэтому мы берём его. И последнее — Keras, встроенная в Tensorflow библиотека, которая умеет обучать нейросети.
Теперь создадим самую простую модель:
model = tf.keras.Sequential([keras.layers.Dense(units=1, input_shape=[1])])
Разберём код подробнее. Sequential — это тип нейросети, означающий, что процесс обучения будет последовательным. Это стандартный процесс обучения для простых нейросетей: в нём она сначала делает предсказания, затем тестирует их и сравнивает с результатом, а в конце — корректирует ошибки.
keras.layers.Dense — указывает на то, что мы хотим создать слой в нашей модели. Слой — это место, куда мы будем складывать нейроны, которые запоминают информацию об ошибках и которые отвечают за «умственные способности» нейросети. Dense — это тип слоя, который использует специальные алгоритмы для обучения.
В качестве аргумента нашей нейросети мы передали указания, какой именно она должна быть:
- units=1 означает, что модель состоит из одного нейрона, который будет запоминать информацию о предыдущих предположениях;
- input_shape=[1] говорит о том, что на вход будет подаваться одно число, по которому нейросеть будет строить зависимости двух рядов чисел: X и Y.
Модель мы создали, теперь давайте её скомпилируем:
model.compile(optimizer='sgd', loss='mean_squared_error')
Здесь появляются два важных для машинного обучения элемента: функция оптимизации и функция потерь. Обе они нужны, чтобы постепенно стремиться к более точным результатам.
Функция потерь анализирует, насколько правильно нейросеть дала предсказание. А функция оптимизации исправляет эти предсказания в сторону более корректных результатов.
Мы использовали стандартные функции для большинства моделей — sgd и mean_squared_error. sgd — это метод оптимизации, который работает на формулах математического анализа. Он помогает скорректировать формулу, чтобы прийти к правильной. mean_squared_error — это функция, которая вычисляет, насколько сильно отличаются полученные результаты по формуле, предложенной нейросетью, от настоящих результатов. Эта функция тоже участвует в корректировке формулы.
Теперь давайте зададим наборы данных:
xs = np.array([-1.0, 0.0, 1.0, 2.0, 3.0, 4.0], dtype=float) ys = np.array([-4.0, 1.0, 6.0, 11.0, 16.0, 21.0], dtype=float)
Как видно, это обычные массивы чисел, которые мы передадим модели на обучение:
model.fit(xs, ys, epochs=500)
Функция fit как раз занимается обучением. Она берёт набор входных данных — xs — и сопоставляет с набором правильных результатов — ys. И так нейросеть обучается в течение 500 итераций — epochs=500. Мы использовали 500 итераций, чтобы наверняка прийти к правильному результату. Суть простая: чем больше итераций обучения, тем точнее будут результаты (однако улучшение точности с каждым повтором будет всё меньше и меньше).
На каждой итерации модель проходит следующие шаги:
- берёт весь наш набор входных данных;
- пытается сделать предсказание для каждого элемента;
- сравнивает результат с корректным результатом;
- оптимизирует модель, чтобы давать более точные прогнозы.
Скриншот: Skillbox Media
Можно заметить, что на каждой итерации TensorFlow выводит, насколько нейросеть сильно ошиблась — loss. Если это число уменьшается, то есть стремится к нулю, значит, она действительно обучается и с каждым шагом улучшает свои прогнозы.
Теперь давайте что-нибудь предскажем и поймём, насколько точно наша нейросеть обучилась:
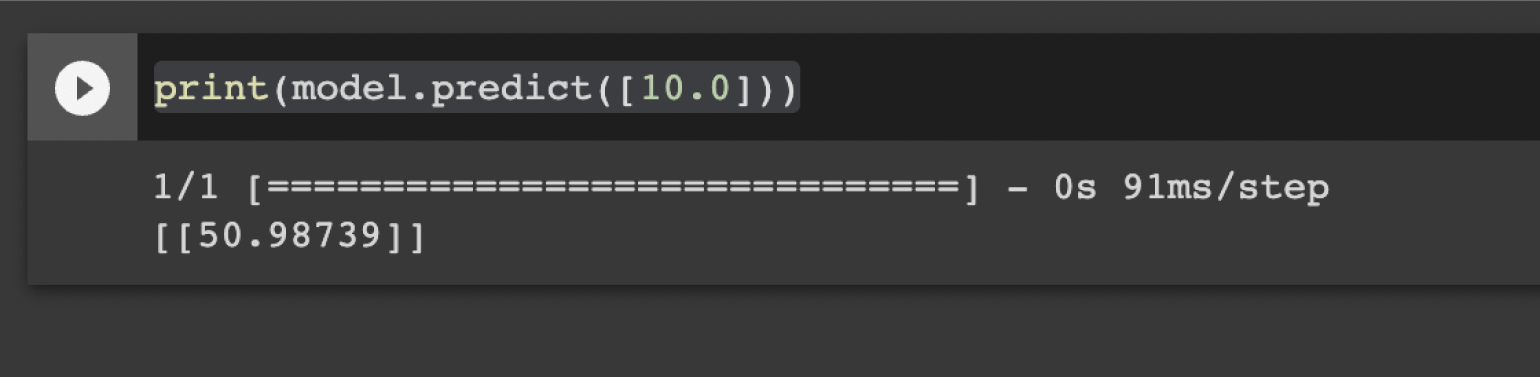
print(model.predict([10.0]))
Мы вызываем у модели метод predict, который получает на вход элемент для предсказания. Результат будет таким:
Скриншот: Skillbox Media
Получилось странно — мы ожидали, что будет число 51 (потому что подставили 10 в выражение 5X + 1) — но на выходе нейросеть выдала число 50.98739. А всё потому, что модель нашла очень близкую, но не до конца точную формулу — например, 4.891X + 0.993. Это одна из особенностей машинного обучения.
А ещё многое зависит от выбранного метода оптимизации — то есть того, как нейросеть корректирует формулу, чтобы прийти к нужным результатам. В библиотеке TensorFlow можно найти разные способы оптимизации, и на выходе каждой из них результаты могут различаться. Однако эта тема выходит за рамки нашей статьи — здесь уже необходимо достаточно глубоко погружаться в процесс машинного обучения и разбираться, как именно устроена оптимизация.
Если вы вдруг подумали, что можно просто увеличить число итераций и точность станет выше, то это справедливо лишь отчасти. У каждого метода оптимизации есть своя точность, до которой нейросеть может дойти. Например, она может вычислять результат с точностью до 0.00000001, однако абсолютно верным и точным результат не будет никогда. А значит, и абсолютно точного значения формулы мы никогда не получим — просто из-за погрешности вычислений и особенности функционирования компьютеров. Но если условно установить число итераций в миллиард, можно получить примерно такую формулу:
4.9999999999997X + 0.9999999999991
Она очень близка к настоящей, хотя и не равна ей. Поэтому математики и специалисты по машинному обучению решили, что будут считать две формулы равными, если значения их вычислений меньше, чем заранее заданная величина погрешности — например, 0.0000001. И если мы подставим в формулу выше и в настоящую вместо X число 5, то получим следующее:
5 · 5 + 1 = 26
4.9999999997 · 5 + 0.9999999991 = 25.9999999976
Если мы из первого числа вычтем второе, то получим:
26 — 25.9999999976 = 0.0000000024
А так как изначально мы сказали, что два числа будут равны, если разница между ними меньше 0.0000001, то обе формулы могут считаться идентичными, потому что получившаяся у нас на практике погрешность 0.0000000024 меньше допустимого значения, о котором мы договорились, — то есть 0.0000001. Вот такая интересная математика.
В этой статье мы рассмотрим, как создать собственную простейшую нейронную сеть с помощью языка программирования «Питон». Мы не только создадим нейронную сеть с нуля, но и не будем использовать никаких библиотек. И займёт это всё не более девяти строчек кода на «Питоне».
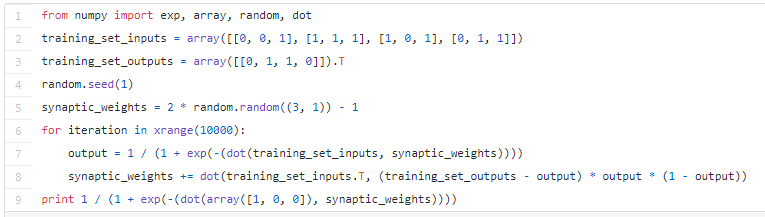
Вот как выглядит код простейшей нейронной сети на «Питоне»:
Теперь давайте поговорим о том, как это получилось, а также посмотрим на расширенную версию кода. Внимательно изучив эту статью, вы сможете и сами написать свою нейронную сеть на «Питоне».
Что такое нейронная сеть (Neural Network)?
Прежде чем продолжить, вспомним, что из себя представляет нейронная сеть. Мы знаем, что мозг человека состоит из 100 млрд. клеток, которые мы называем нейроны. Они соединены синапсами, а когда нужное количество синаптических входов возбуждено, нейрон тоже возбуждается. Этот процесс учёные называют «мышлением».
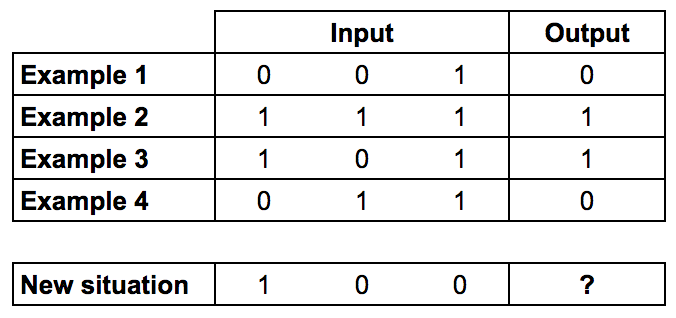
Процесс можно смоделировать, если создать нейронную сеть на ПК. Причём нет необходимости моделировать сложнейшую модель мозга человека полностью, хватит лишь нескольких основных правил. Чтобы упростить реализацию, будем использовать классические матрицы и создадим модель из 3-х входных и одного выходного сигналов. И попробуем выполнить тренировку нейрона.
Первые 4 примера — это тренировочная выборка.
Обратите внимание, что значение столбца Output всегда равно значению самой левой колонки из столбца Input. Это значит, что правильный ответ в нашем случае будет равен 1.
Обучаем нейронную сеть
Теперь давайте добавим каждому входу вес (положительное или отрицательное число). Вход с большим отрицательным либо большим положительным весом существенно повлияет на выход нейрона. Но до начала обучения надо установить каждый вес случайной величиной. После этого можно приступать:
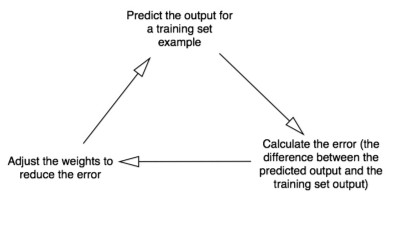
1. Возьмём входные данные из примера, скорректируем значения по весам и передадим их по формуле расчёта выхода нейрона.
2. Вычислим ошибочное значение (это, по сути, разница между выходом нейрона и желаемым нами выходом в примере используемого нами тренировочного набора).
3. Немного отрегулируем вес с учётом направления ошибки.
4. Повторим данный процесс десять тысяч раз.
По итогу вес нейрона достигает оптимального значения для нашего обучающего набора. Теперь, если позволить нейрону «подумать», он сделает хороший прогноз.
Формулируем расчёт выхода нейрона
Теперь посмотрим на формулу расчёта выхода нейрона. Поначалу возьмём взвешенную сумму входов:
Потом выполним нормализацию, и результат будет между 0 и 1. Теперь задействуем математическую функцию Sigmoid:
Функция Sigmoid нарисует S-образную кривую:
Подставим 1-е уравнение во 2-е и получим интересующую нас формулу выхода:
Правда, пороговый потенциал использовать не будем в целях упрощения примера.
Формула корректировки веса
В процессе тренировочного цикла мы выполняем корректировку весов. Но насколько происходит корректировка? Тут подойдёт формула взвешенной ошибки:
Формула позволяет выполнять корректировку пропорционально величине ошибки. Также умножение происходит на входное значение, равное 0 либо 1. Когда входное значение будет равно 0, вес корректироваться не будет. Дополнительно мы выполняем умножение на градиент сигмовидной кривой. Что тут нужно учесть:
1. Сигмовидная кривая использовалась для расчёта выхода нейрона.
2. При больших числах кривая имеет небольшой градиент.
Если нейрон уверен в правильности существующего веса, он не хочет корректировать его слишком сильно. Умножение на градиент кривой именно это и делает.
Градиент Сигмоды образуется, если будем выполнять расчёты взятием производной:
Если мы вычтем 2-е уравнение из 1-го, то получим необходимую итоговую формулу:
Есть и другие формулы, позволяющие нейрону обучаться быстрее, но указанная нами является максимально простой.
Пример нейронной сети на Python
Было заявлено, что библиотеки задействоваться не будут. Так-то оно так, но четыре метода из numpy импортировать придётся:
— exp — для экспоненцирования;
— dot — для перемножения матриц;
— array — для создания матрицы;
— random — для генерации случайных чисел.
Тот же array() можно применять для представления обучающего множества.
В нашем случае “.T” является функцией транспонирования матриц.
Раз мы готовы создать более красивую версию исходного кода, приступим. Обратите внимание, что на каждой итерации одновременно обрабатывается вся тренировочная выборка.
Этот код вы найдёте и по ссылке на GitHub. Если будете работать с Python 3, замените лишь xrange на range.
Итог
Давайте запустим нейронную сеть через терминал:
Результат должен быть приблизительно следующим:
Если у вас всё получилось, поздравляем — вы только что написали простейшую нейросеть!
Смотрите, изначально нейросеть присваивала себе случайные значения весов, потом она обучалась с помощью тренировочного набора. Далее она рассмотрела новую ситуацию [1, 0, 0], предсказав 0.99993704. Так как правильный ответ равен единице, можно сказать, что предсказание получилось довольно точным.
Источник — How to build a simple neural network in 9 lines of Python code.
Поначалу может показаться, что всё просто. Но если вы хотите освоить работу нейронных сетей на практике и всерьёз, стоит подумать о специализированных курсах. На них вы узнаете про нейронные сети гораздо больше, ведь простого чтения статей из интернета явно недостаточно. Вы разберёте нейросети прямого распространения, обратного распространения, скрытого слоя и т. д. и т. п., узнаете про функции потерь, функцию активации, обучение с подкреплением, ознакомитесь с другой важной информацией. Записаться на курс по нейронным сетям в качестве студента можно по ссылке ниже:
https://otus.ru/lessons/deep-learning-engineer/.
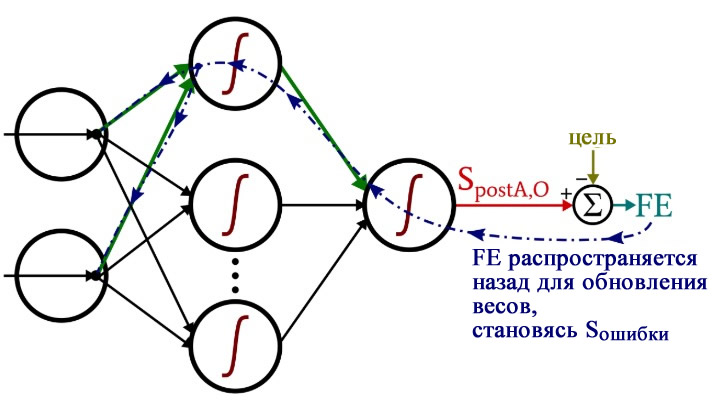
Руководство для начинающих, чтобы понять внутреннюю работу глубокого обучения
Beginner’s Guide of Deep Learning
Мотивация: как часть моего личного пути, чтобы получить лучшее понимание глубокого обучения, я решил построить нейронную сеть с нуля без библиотеки глубокого обучения, такой как TensorFlow. Я считаю, что понимание внутренней работы нейронной сети важно для любого начинающего специалиста по данным.
Эта статья содержит то, что я узнал, и, надеюсь, это будет полезно и для вас!
Что такое нейронная сеть?
В большинстве вводных текстов по нейронным сетям приводятся аналогии с мозгом при их описании. Не углубляясь в аналогии с мозгом, я считаю, что проще описать нейронные сети как математическую функцию, которая отображает заданный вход в желаемый результат.
Нейронные сети состоят из следующих компонентов
- Входной слой , х
- Произвольное количество скрытых слоев
- Выходной слой , сечение ■
- Набор весов и смещений между каждым слоем, W и B
- Выбор функции активации для каждого скрытого слоя, σ . В этом уроке мы будем использовать функцию активации Sigmoid.
На диаграмме ниже показана архитектура двухслойной нейронной сети ( обратите внимание, что входной слой обычно исключается при подсчете количества слоев в нейронной сети )
Архитектура двухслойной нейронной сети
Создать класс нейросети в Python просто.
class NeuralNetwork:
def __init__(self, x, y):
self.input = x
self.weights1 = np.random.rand(self.input.shape[1],4)
self.weights2 = np.random.rand(4,1)
self.y = y
self.output = np.zeros(y.shape)
Обучение нейронной сети
Выход ŷ простой двухслойной нейронной сети:
Вы можете заметить, что в приведенном выше уравнении весовые коэффициенты W и смещения b являются единственными переменными, которые влияют на результат ŷ.
Естественно, правильные значения весов и смещений определяют силу прогнозов. Процесс тонкой настройки весов и смещений из входных данных известен как обучение нейронной сети.
Каждая итерация учебного процесса состоит из следующих шагов:
- Расчет прогнозируемого выхода known , известный как прямая связь
- Обновление весов и уклонов, известных как обратное распространение
Последовательный график ниже иллюстрирует процесс.
прогнозирование
Как мы видели на приведенном выше последовательном графике, прямая связь — это просто простое исчисление, и для базовой двухслойной нейронной сети результат работы нейронной сети:
Давайте добавим функцию обратной связи в наш код Python, чтобы сделать именно это. Обратите внимание, что для простоты мы приняли смещения равными 0.
class NeuralNetwork:
def __init__(self, x, y):
self.input = x
self.weights1 = np.random.rand(self.input.shape[1],4)
self.weights2 = np.random.rand(4,1)
self.y = y
self.output = np.zeros(self.y.shape)
def feedforward(self):
self.layer1 = sigmoid(np.dot(self.input, self.weights1))
self.output = sigmoid(np.dot(self.layer1, self.weights2))
Однако нам все еще нужен способ оценить «доброту» наших прогнозов (т. Е. Насколько далеки наши прогнозы)? Функция потерь позволяет нам делать именно это.
Функция потери
Есть много доступных функций потерь, и природа нашей проблемы должна диктовать наш выбор функции потерь. В этом уроке мы будем использовать простую ошибку суммы квадратов в качестве нашей функции потерь.
То есть ошибка суммы квадратов — это просто сумма разности между каждым прогнозируемым значением и фактическим значением. Разница возводится в квадрат, поэтому мы измеряем абсолютное значение разницы.
Наша цель в обучении — найти лучший набор весов и смещений, который минимизирует функцию потерь.
обратное распространение
Теперь, когда мы измерили ошибку нашего прогноза (потери), нам нужно найти способ распространить ошибку назад и обновить наши веса и отклонения.
Чтобы узнать соответствующую сумму, с помощью которой можно корректировать веса и смещения, нам необходимо знать производную функции потерь по весам и смещениям .
Напомним из исчисления, что производная функции — это просто наклон функции.
Если у нас есть производная, мы можем просто обновить веса и смещения, увеличивая / уменьшая ее (см. Диаграмму выше). Это известно как градиентный спуск .
Однако мы не можем напрямую рассчитать производную функции потерь по весам и смещениям, потому что уравнение функции потерь не содержит весов и смещений. Поэтому нам нужно цепное правило, чтобы помочь нам его вычислить.
Уф! Это было некрасиво, но оно позволяет нам получить то, что нам нужно — производную (наклон) функции потерь по отношению к весам, чтобы мы могли соответствующим образом корректировать веса.
Теперь, когда у нас это есть, давайте добавим функцию обратного распространения в наш код Python.
class NeuralNetwork:
def __init__(self, x, y):
self.input = x
self.weights1 = np.random.rand(self.input.shape[1],4)
self.weights2 = np.random.rand(4,1)
self.y = y
self.output = np.zeros(self.y.shape)
def feedforward(self):
self.layer1 = sigmoid(np.dot(self.input, self.weights1))
self.output = sigmoid(np.dot(self.layer1, self.weights2))
def backprop(self):
# application of the chain rule to find derivative of the loss function with respect to weights2 and weights1
d_weights2 = np.dot(self.layer1.T, (2*(self.y - self.output) * sigmoid_derivative(self.output)))
d_weights1 = np.dot(self.input.T, (np.dot(2*(self.y - self.output) * sigmoid_derivative(self.output), self.weights2.T) * sigmoid_derivative(self.layer1)))
# update the weights with the derivative (slope) of the loss function
self.weights1 += d_weights1
self.weights2 += d_weights2
Для более глубокого понимания применения исчисления и правила цепочки в обратном распространении я настоятельно рекомендую этот урок от 3Blue1Brown.
Собираем все вместе
Теперь, когда у нас есть полный код Python для выполнения обратной связи и обратного распространения, давайте применим нашу нейронную сеть на примере и посмотрим, насколько хорошо она работает.
Наша нейронная сеть должна изучить идеальный набор весов для представления этой функции. Обратите внимание, что для нас не совсем просто вычислить вес только одним осмотром.
Давайте обучим нейронную сеть для 1500 итераций и посмотрим, что произойдет. Глядя на график потерь на итерацию ниже, мы ясно видим, что потери монотонно уменьшаются до минимума. Это согласуется с алгоритмом градиентного спуска, который мы обсуждали ранее.
Давайте посмотрим на окончательный прогноз (выход) из нейронной сети после 1500 итераций.
Мы сделали это! Наш алгоритм обратной связи и обратного распространения успешно обучил нейронную сеть, и прогнозы сошлись на истинных значениях.
Обратите внимание, что существует небольшая разница между прогнозами и фактическими значениями. Это желательно, поскольку это предотвращает переоснащение и позволяет нейронной сети лучше обобщать невидимые данные.
Что дальше?
К счастью для нас, наше путешествие не закончено. Еще многое предстоит узнать о нейронных сетях и глубоком обучении. Например:
- Какую другую функцию активации мы можем использовать, кроме функции Sigmoid?
- Использование скорости обучения при обучении нейронной сети
- Использование сверток для задач классификации изображений
Я скоро напишу больше на эти темы, так что следите за мной на Medium и следите за ними!
Последние мысли
Я, конечно, многому научился писать свою собственную нейронную сеть с нуля.
Хотя библиотеки глубокого обучения, такие как TensorFlow и Keras, позволяют легко создавать глубокие сети без полного понимания внутренней работы нейронной сети, я считаю, что для начинающего ученого-исследователя полезно получить более глубокое понимание нейронных сетей.
3
2
голоса
Рейтинг статьи
Добавлено 1 февраля 2020 в 17:16
Данная статья шаг за шагом проведет вас по программе на Python, которая позволит нам обучить нейронную сеть и выполнить сложную классификацию.
Это 12-я статья в серии о разработке нейронных сетей. С остальными статьями вы можете ознакомиться выше, в меню с содержанием.
В данной статье мы применим знания, полученные нами при изучении нейронных сетей перцептрон, и узнаем, как реализовать нейросеть на знакомом языке: Python.
Разработка понятного кода на Python для нейронных сетей
Недавно я просмотрел немало онлайн-ресурсов по нейронным сетям, и, хотя, несомненно, в них есть много полезной информации, я не был удовлетворен найденными мною программными реализациями. Они всегда были или слишком сложными, или недостаточно интуитивно понятными. Когда я писал свою нейронную сеть на Python, я на самом деле хотел сделать что-то, что могло бы помочь людям узнать о том, как работает система, и как теория нейронных сетей переводится на язык программных инструкций.
Однако иногда между ясностью и эффективностью кода существует обратная зависимость. Программа, которую мы обсудим в этой статье, однозначно не оптимизирована для быстрой работы. Оптимизация является серьезной проблемой в области нейронных сетей; реальные приложения могут потребовать огромного количества обучения, и, следовательно, тщательная оптимизация может привести к значительному сокращению времени обработки. Тем не менее, для простых экспериментов, подобных тем, которые мы будем проводить, обучение не займет много времени, и нет оснований делать упор на методиках программирования, которые способствуют скорости, а не простоте и понятности.
Полный код программы на Python приведен в конце статьи. Код выполняет как обучение, так и проверку. Данная статья посвящена обучению, а валидацию мы обсудим позже. В любом случае, во фрагменте программы, выполняющем проверку, не так много функционала, который не покрыт во фрагменте, выполняющем обучение.
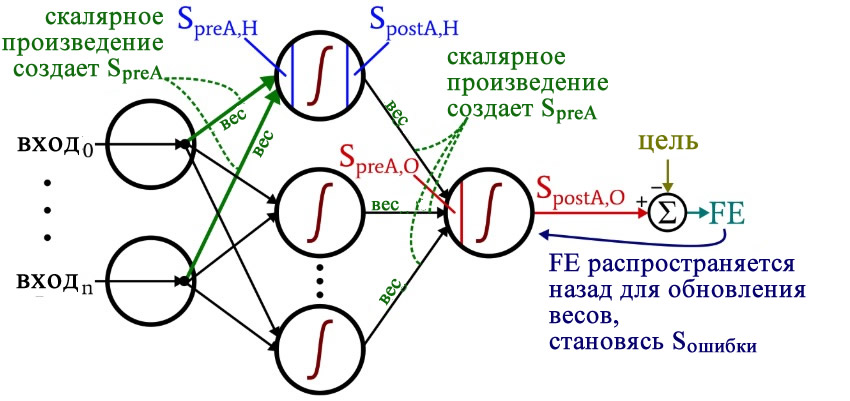
Размышляя над кодом, вы, возможно, захотите оглянуться на немного сумбурную, но очень информативную диаграмму архитектуры плюс терминологии, которую я представил в части 10.
Подготовка функций и переменных
import pandas
import numpy as np
def logistic(x):
return 1.0/(1 + np.exp(-x))
def logistic_deriv(x):
return logistic(x) * (1 - logistic(x))
LR = 1
I_dim = 3
H_dim = 4
epoch_count = 1
#np.random.seed(1)
weights_ItoH = np.random.uniform(-1, 1, (I_dim, H_dim))
weights_HtoO = np.random.uniform(-1, 1, H_dim)
preActivation_H = np.zeros(H_dim)
postActivation_H = np.zeros(H_dim)Библиотека NumPy широко используется для расчетов в нейросети, а библиотека Pandas дает мне удобный способ импортировать данные обучения из файла Excel.
Как вы уже знаете, для активации мы используем функцию логистической сигмоиды. Для расчета значений постактивации нам нужна сама логистическая функция, а для обратного распространения необходима производная логистической функции.
Затем мы выбираем скорость обучения, размерность входного слоя, размерность скрытого слоя и количество эпох. Для реальных нейронных сетей важно обучение в течение нескольких эпох, потому что это позволяет вам извлечь больше информации из ваших обучающих данных. Когда вы генерируете обучающие данные в Excel, вам не нужно запускать несколько эпох, потому что вы можете легко создать больше обучающих выборок.
Функция np.random.uniform() заполняет наши две матрицы весов случайными значениями от –1 до +1 (обратите внимание, что матрица весов между скрытым и выходным слоями на самом деле представляет собой просто массив, поскольку у нас только один выходной узел). Оператор np.random.seed(1) приводит к тому, что случайные значения становятся одинаковыми при каждом запуске программы. Начальные значения весов могут оказать существенное влияние на конечную производительность обученной сети, поэтому, если вы пытаетесь оценить, как другие переменные улучшают или ухудшают производительность, вы можете раскомментировать эту инструкцию и тем самым устранить влияние случайной инициализации весовых коэффициентов.
И в конце я создаю пустые массивы для значений преактивации и постактивации в скрытом слое.
Импорт обучающих данных
training_data = pandas.read_excel('MLP_Tdata.xlsx')
target_output = training_data.output
training_data = training_data.drop(['output'], axis=1)
training_data = np.asarray(training_data)
training_count = len(training_data[:,0])Это та же процедура, которую я использовал в части 3. Я импортирую обучающие данные из Excel, отделяю целевые значения в столбце «output», удаляю столбец «output», преобразую обучающие данные в матрицу NumPy и сохраняю количество обучающих выборок в переменной training_count.
Обработка прямого распространения
Вычисления, которые создают выходное значение, и в которых данные перемещаются слева направо на типовой схеме нейронной сети, составляют фрагмент «прямого распространения» работы системы. Вот код «прямого распространения»:
#####################
# обучение
#####################
for epoch in range(epoch_count):
for sample in range(training_count):
for node in range(H_dim):
preActivation_H[node] = np.dot(training_data[sample,:], weights_ItoH[:, node])
postActivation_H[node] = logistic(preActivation_H[node])
preActivation_O = np.dot(postActivation_H, weights_HtoO)
postActivation_O = logistic(preActivation_O)
FE = postActivation_O - target_output[sample]Первый цикл for позволяет нам проходить через несколько эпох. Внутри каждой эпохи, во втором цикле for, поочередно проходя по выборкам, мы вычисляем выходное значение для каждой выборки (то есть сигнал постактивации выходного узла). В третьем цикле for мы обращаемся индивидуально к каждому скрытому узлу, используя скалярное произведение для генерирования сигнала преактивации и функцию активации для генерирования сигнала постактивации.
После этого мы готовы вычислить сигнал преактивации для выходного узла (снова используя скалярное произведение), и мы применяем функцию активации для генерирования сигнала постактивации. Затем, чтобы вычислить итоговую ошибку, мы вычитаем целевое значение из значения полученного сигнала постактивации выходного узла.
Обратное распространение
После того, как мы выполнили расчеты для прямого распространения, настало время изменить направление. Во фрагменте программы с обратным распространением мы перемещаемся к весам от скрытых узлов к выходному узлу, а затем к весам от входного слоя к скрытому слою, перенося при этом информацию об ошибке для эффективного обучения сети.
for H_node in range(H_dim):
S_error = FE * logistic_deriv(preActivation_O)
gradient_HtoO = S_error * postActivation_H[H_node]
for I_node in range(I_dim):
input_value = training_data[sample, I_node]
gradient_ItoH = S_error * weights_HtoO[H_node] * logistic_deriv(preActivation_H[H_node]) * input_value
weights_ItoH[I_node, H_node] -= LR * gradient_ItoH
weights_HtoO[H_node] -= LR * gradient_HtoOУ нас есть два слоя для циклов for: один для весовых коэффициентов между скрытым и выходным слоями и один для весовых коэффициентов между входным и скрытым слоями. Сначала мы генерируем сигнал ошибки (Sошибки, S_error), который нам нужен для вычисления обоих градиентов, gradient_HtoO (от скрытого слоя к выходному) и gradient_ItoH (от входного слоя к скрытому), а затем мы обновляем весовые коэффициенты, вычитая градиент, умноженный на скорость обучения.
Обратите внимание, как веса между входным и скрытым слоями обновляются внутри цикла для значений между скрытым и выходным слоями. Мы начинаем с сигнала ошибки, который ведет обратно к одному из скрытых узлов, затем распространяем этот сигнал ошибки на все входные узлы, которые подключены к одному конкретному скрытому узлу:
После того, как все весовые коэффициенты (как ItoH (от входного слоя к скрытому), так и HtoO (от скрытого слоя к выходному)), связанные с этим одним скрытым узлом, были обновлены, мы возвращаемся к началу и начинаем снова для следующего скрытого узла.
Также обратите внимание, что веса ItoH модифицируются перед весами HtoO. Мы используем текущий вес HtoO при расчете градиента, поэтому до выполнения расчетов мы не хотим изменять веса HtoO.
Заключение
Интересно задуматься о том, сколько теории ушло в эту относительно короткую программу на Python. Я надеюсь, что этот код на самом деле поможет вам понять, как мы можем программно реализовать нейронную сеть многослойный перцептрон.
Ниже приведен полный код программы.
import pandas
import numpy as np
def logistic(x):
return 1.0/(1 + np.exp(-x))
def logistic_deriv(x):
return logistic(x) * (1 - logistic(x))
LR = 1
I_dim = 3
H_dim = 4
epoch_count = 1
#np.random.seed(1)
weights_ItoH = np.random.uniform(-1, 1, (I_dim, H_dim))
weights_HtoO = np.random.uniform(-1, 1, H_dim)
preActivation_H = np.zeros(H_dim)
postActivation_H = np.zeros(H_dim)
training_data = pandas.read_excel('MLP_Tdata.xlsx')
target_output = training_data.output
training_data = training_data.drop(['output'], axis=1)
training_data = np.asarray(training_data)
training_count = len(training_data[:,0])
validation_data = pandas.read_excel('MLP_Vdata.xlsx')
validation_output = validation_data.output
validation_data = validation_data.drop(['output'], axis=1)
validation_data = np.asarray(validation_data)
validation_count = len(validation_data[:,0])
#####################
# обучение
#####################
for epoch in range(epoch_count):
for sample in range(training_count):
for node in range(H_dim):
preActivation_H[node] = np.dot(training_data[sample,:], weights_ItoH[:, node])
postActivation_H[node] = logistic(preActivation_H[node])
preActivation_O = np.dot(postActivation_H, weights_HtoO)
postActivation_O = logistic(preActivation_O)
FE = postActivation_O - target_output[sample]
for H_node in range(H_dim):
S_error = FE * logistic_deriv(preActivation_O)
gradient_HtoO = S_error * postActivation_H[H_node]
for I_node in range(I_dim):
input_value = training_data[sample, I_node]
gradient_ItoH = S_error * weights_HtoO[H_node] * logistic_deriv(preActivation_H[H_node]) * input_value
weights_ItoH[I_node, H_node] -= LR * gradient_ItoH
weights_HtoO[H_node] -= LR * gradient_HtoO
#####################
# проверка
#####################
correct_classification_count = 0
for sample in range(validation_count):
for node in range(H_dim):
preActivation_H[node] = np.dot(validation_data[sample,:], weights_ItoH[:, node])
postActivation_H[node] = logistic(preActivation_H[node])
preActivation_O = np.dot(postActivation_H, weights_HtoO)
postActivation_O = logistic(preActivation_O)
if postActivation_O > 0.5:
output = 1
else:
output = 0
if output == validation_output[sample]:
correct_classification_count += 1
print('Percentage of correct classifications:')
print(correct_classification_count*100/validation_count)Теги
MLP, Multilayer Perceptron / Многослойный перцептронPythonМашинное обучение / Machine LearningНейросеть / Нейронная сетьОбработка прямого распространенияОбратное распространениеПерцептрон / PerceptronПрограммирование
Что такое машинное обучение и почему это важно?
Машинное обучение — это область искусственного интеллекта, использующая статистические методы, чтобы предоставить компьютерным системам способность «учиться». То есть постепенно улучшать производительность в конкретной задаче, с помощью данных без явного программирования. Хороший пример — то, насколько эффективно (или не очень) Gmail распознает спам или насколько совершеннее стали системы распознавания голоса с приходом Siri, Alex и Google Home.
С помощью машинного обучения решаются следующие задачи:
- Распознавание мошенничества — отслеживание необычных шаблонов в транзакциях кредитных карт или банковских счетов
- Предсказание — предсказание будущей цены акций, курса обмена валюты или криптовалюты
- Распознавание изображений — определение объектов и лиц на картинках
Машинное обучение — огромная область, и сегодня речь пойдет лишь об одной из ее составляющих.
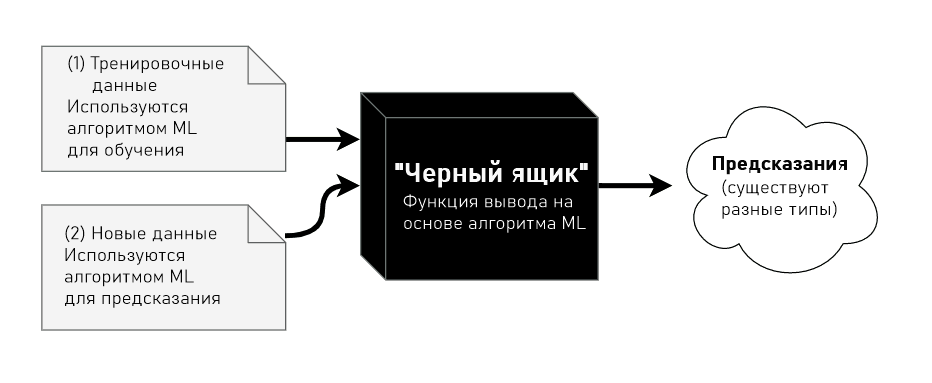
Обучение с учителем
Обучение с учителем — один из видов машинного обучения. Его идея заключается в том, что систему сначала учат понимать прошлые данные, предлагая много примеров конкретной проблемы и желаемый вывод. Затем, когда система «натренирована», ей можно давать новые входные данные для предсказания выводов.
Например, как создать спам-детектор? Один из способов — интуиция. Можно вручную определять правила: например «содержит слово деньги» или «включает фразу Western Union». И пусть иногда такие системы работают, в большинстве случаев все-таки сложно создать или определить шаблоны, опираясь исключительно на интуицию.
С помощью обучения с учителем можно тренировать системы изучать лежащие в основе правила и шаблоны за счет предоставления примеров с большим количеством спама. Когда такой детектор натренирован, ему можно дать новое письмо, чтобы он попытался предсказать, является ли оно спамом.
Обучение с учителем можно использовать для предсказания вывода. Есть два типа проблем, которые решаются с его помощью: регрессия и классификация.
- В регрессионных проблемах мы пытаемся предсказать непрерывный вывод. Например, предсказание цены дома на основе данных о его размере
- В классификационных — предсказываем дискретное число качественных меток. Например, попытка предсказать, является ли письмо спамом на основе количества слов в нем.
Невозможно говорить о машинном обучении с учителем, не затронув модели обучения с учителем. Это как говорить о программировании, не касаясь языков программирования или структур данных. Модели обучения — это те самые структуры, что поддаются тренировке. Их вес (или структура) меняется по мере того, как они формируют понимание того, что нужно предсказывать. Есть несколько видов моделей обучения, например:
- Случайный лес (random forest)
- Наивный байесовский классификатор (naive Bayes)
- Логистическая регрессия (logistic regression)
- Метод k-ближайших соседей (k nearest neighbors)
В этом материале в качестве модели будет использоваться нейронная сеть.
Понимание работы нейронных сетей
Нейронные сети получили такое название, потому что их внутренняя структура должна имитировать человеческий мозг. Последний состоит из нейронов и синапсов, которые их соединяют. В момент стимуляции нейроны «активируют» другие с помощью электричества.
Каждый нейрон «активируется» в первую очередь за счет вычисления взвешенной суммы вводных данных и последующего результата с помощью результирующей функции. Когда нейрон активируется, он в свою очередь активирует остальные, которые выполняют похожие вычисления, вызывая цепную реакцию между всеми нейронами всех слоев.
Стоит отметить, что пусть нейронные сети и вдохновлены биологическими, сравнивать их все-таки нельзя.
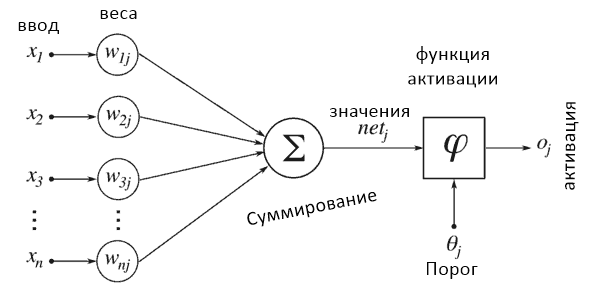
- Эта диаграмма иллюстрирует процесс активации, через который проходит каждый нейрон. Рассмотрим схему слева направо.
- Все вводные данные (числовые значения) из входящих нейронов считываются. Они определяются как x1…xn.
- Каждый ввод умножается на взвешенную сумму, ассоциированную с этим соединением. Ассоциированные веса обозначены как W1j…Wnj.
- Все взвешенные вводы суммируются и передаются активирующей функции. Она читает этот ввод и трансформирует его в числовое значение k-ближайших соседей.
- В итоге числовое значение, которое возвращает эта функция, будет вводом для другого нейрона в другом слое.
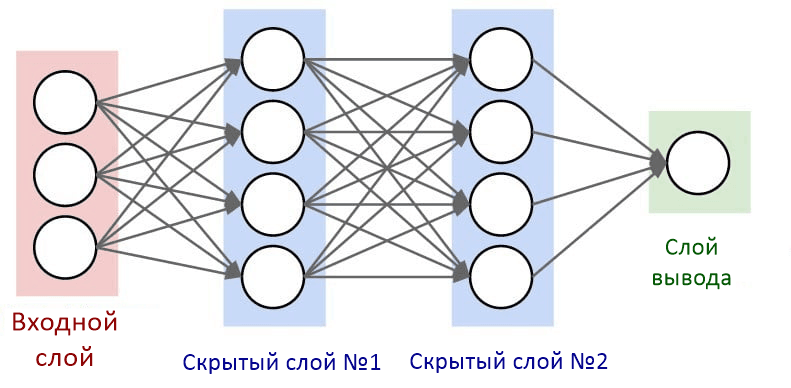
Слои нейронной сети
Нейроны внутри нейронной сети организованы в слои. Слои — это способ создать структуру, где каждый содержит 1 или большее количество нейронов. В нейронной сети обычно 3 или больше слоев. Также всегда определяются 2 специальных слоя, которые выполняют роль ввода и вывода.
- Слой ввода является точкой входа в нейронную сеть. В рамках программировании его можно воспринимать как аргумент функции.
- Вывод — это результат работы нейронной сети. В терминах программирования это возвращаемое функцией значение.
Слои между ними описываются как «скрытые слои». Именно там происходят все вычисления. Все слои в нейронной сети кодируются как признаковые описания.
Выбор количества скрытых слоев и нейронов
Нет золотого правила, которым стоит руководствоваться при выборе количества слоев и их размера (или числа нейронов). Как правило, стоит попробовать как минимум 1 такой слой и дальше настраивать размер, проверяя, что работает лучше всего.
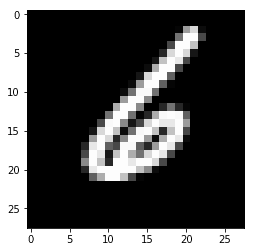
Использование библиотеки Keras для тренировки простой нейронной сети, которая распознает рукописные цифры
Программистам на Python нет необходимости заново изобретать колесо. Такие библиотеки, как Tensorflow, Torch, Theano и Keras уже определили основные структуры данных для нейронной сети, оставив необходимость лишь декларативно описать структуру нейронной сети.
Keras предоставляет еще и определенную свободу: возможность выбрать количество слоев, число нейронов, тип слоя и функцию активации. На практике элементов довольно много, но в этот раз обойдемся более простыми примерами.
Как уже упоминалось, есть два специальных уровня, которые должны быть определены на основе конкретной проблемы: размер слоя ввода и размер слоя вывода. Все остальные «скрытые слои» используются для изучения сложных нелинейных абстракций задачи.
В этом материале будем использовать Python и библиотеку Keras для предсказания рукописных цифр из базы данных MNIST.
Запуск Jupyter Notebook локально
Если вы еще не работали с Jupyter Notebook, сначало изучите Руководство по Jupyter Notebook для начинающих
Список необходимых библиотек:
- numpy
- matplotlib
- sklearn
- tensorflow
Запуск из интерпретатора Python
Для запуска чистой установки Python (любой версии старше 3.6) установите требуемые модули с помощью pip.
Рекомендую (но не обязательно) запускать код в виртуальной среде.
!pip install matplotlib
!pip install sklearn
!pip install tensorflow
Если эти модули установлены, то теперь можно запускать весь код в проекте.
Импортируем модули и библиотеки:
import numpy as np
import matplotlib.pyplot as plt
import gzip
from typing import List
from sklearn.preprocessing import OneHotEncoder
import tensorflow.keras as keras
from sklearn.model_selection import train_test_split
from sklearn.metrics import confusion_matrix
import itertools
%matplotlib inline
База данных MNIST
MNIST — это огромная база данных рукописных цифр, которая используется как бенчмарк и точка знакомства с машинным обучением и системами обработки изображений. Она идеально подходит, чтобы сосредоточиться именно на процессе обучения нейронной сети. MNIST — очень чистая база данных, а это роскошь в мире машинного обучения.
Цель
Натренировать систему, классифицировать каждое соответствующим ярлыком (изображенной цифрой). С помощью набора данных из 60 000 изображений рукописных цифр (представленных в виде изображений 28х28 пикселей, каждый из которых является градацией серого от 0 до 255).
Набор данных
Набор данных состоит из тренировочных и тестовых данных, но для упрощения здесь будет использоваться только тренировочный. Вот так его загрузить:
%%bash
rm -Rf train-images-idx3-ubyte.gz
rm -Rf train-labels-idx1-ubyte.gz
wget -q http://yann.lecun.com/exdb/mnist/train-images-idx3-ubyte.gz
wget -q http://yann.lecun.com/exdb/mnist/train-labels-idx1-ubyte.gz
Чтение меток
Есть 10 цифр: (0-9), поэтому каждая метка должна быть цифрой от 0 до 9. Загруженный файл, train-labels-idx1-ubyte.gz, кодирует метки следующим образом:
Файл ярлыка тренировочного набора (train-labels-idx1-ubyte):
| [offset] | [type] | [value] | [description] |
|---|---|---|---|
| 0000 | 32 bit integer | 0x00000801(2049) | magic number (MSB first) |
| 0004 | 32 bit integer | 60000 | number of items |
| 0008 | unsigned byte | ?? | label |
| 0009 | unsigned byte | ?? | label |
| …… | …… | …… | …… |
| xxxx | unsigned byte | ?? | label |
Значения меток от 0 до 9.
Первые 8 байт (или первые 2 32-битных целых числа) можно пропустить, потому что они содержат метаданные файлы, необходимые для низкоуровневых языков программирования. Для парсинга файла нужно проделать следующие операции:
- Открыть файл с помощью библиотеки gzip, чтобы его можно было распаковать
- Прочитать весь массив байтов в память
- Пропустить первые 8 байт
- Перебирать каждый байт и приводить его к целому числу
Примечание: если этот файл из непроверенного источника, понадобится куда больше проверок. Но предположим, что этот конкретный является надежным и подходит для целей материала.
with gzip.open('train-labels-idx1-ubyte.gz') as train_labels:
data_from_train_file = train_labels.read()
# Пропускаем первые 8 байт
label_data = data_from_train_file[8:]
assert len(label_data) == 60000
# Конвертируем каждый байт в целое число.
# Это будет число от 0 до 9
labels = [int(label_byte) for label_byte in label_data]
assert min(labels) == 0 and max(labels) == 9
assert len(labels) == 60000
Чтение изображений
| [offset] | [type] | [value] | [description] |
|---|---|---|---|
| 0000 | 32 bit integer | 0x00000803(2051) | magic number |
| 0004 | 32 bit integer | 60000 | number of images |
| 0008 | 32 bit integer | 28 | number of rows |
| 0012 | 32 bit integer | 28 | number of columns |
| 0016 | unsigned byte | ?? | pixel |
| 0017 | unsigned byte | ?? | pixel |
| …… | …… | …… | …… |
| xxxx | unsigned byte | ?? | pixel |
Чтение изображений немного отличается от чтения меток. Первые 16 байт содержат уже известные метаданные. Их можно пропустить и переходить сразу к чтению изображений. Каждое из них представлено в виде массива 28*28 из байтов без знака. Все что требуется — читать по одному изображению за раз и сохранять их в массив.
SIZE_OF_ONE_IMAGE = 28 ** 2
images = []
# Перебор тренировочного файла и читение одного изображения за раз
with gzip.open('train-images-idx3-ubyte.gz') as train_images:
train_images.read(4 * 4)
ctr = 0
for _ in range(60000):
image = train_images.read(size=SIZE_OF_ONE_IMAGE)
assert len(image) == SIZE_OF_ONE_IMAGE
# Конвертировать в NumPy
image_np = np.frombuffer(image, dtype='uint8') / 255
images.append(image_np)
images = np.array(images)
images.shape
Вывод: (60000, 784)
В списке 60000 изображений. Каждое из них представлено битовым вектором размером SIZE_OF_ONE_IMAGE. Попробуем построить изображение с помощью библиотеки matplotlib:
def plot_image(pixels: np.array):
plt.imshow(pixels.reshape((28, 28)), cmap='gray')
plt.show()
plot_image(images[25])
Кодирование меток изображения с помощью One-hot encoding
Будем использовать one-hot encoding для превращения целевых меток в вектор.
labels_np = np.array(labels).reshape((-1, 1))
encoder = OneHotEncoder(categories='auto')
labels_np_onehot = encoder.fit_transform(labels_np).toarray()
labels_np_onehot
array([[0., 0., 0., ..., 0., 0., 0.],
[1., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
...,
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 1., 0.]])
Были успешно созданы входные данные и векторный вывод, который будет поступать на входной и выходной слои нейронной сети. Вектор ввода с индексом i будет отвечать вектору вывода с индексом i.
Вводные данные:
labels_np_onehot[999]
Вывод:
array([0., 0., 0., 0., 0., 0., 1., 0., 0., 0.])
Вводные данные:
plot_image(images[999])
Вывод:
В примере выше явно видно, что изображение с индексом 999 представляет цифру 6. Ассоциированный с ним вектор содержит 10 цифр (поскольку имеется 10 меток), а цифра с индексом 6 равно 1. Это значит, что метка правильная.
Разделение датасета на тренировочный и тестовый
Для проверки того, что нейронная сеть была натренирована правильно, берем определенный процент тренировочного набора (60 000 изображений) и используем его в тестовых целях.
Вводные данные:
X_train, X_test, y_train, y_test = train_test_split(images, labels_np_onehot)
print(y_train.shape)
print(y_test.shape)
(45000, 10)
(15000, 10)
Здесь видно, что весь набор из 60 000 изображений бал разбит на два: один с 45 000, а другой с 15 000 изображений.
Тренировка нейронной сети с помощью Keras
model = keras.Sequential()
model.add(keras.layers.Dense(input_shape=(SIZE_OF_ONE_IMAGE,), units=128, activation='relu'))
model.add(keras.layers.Dense(10, activation='softmax'))
model.summary()
model.compile(optimizer='sgd',
loss='categorical_crossentropy',
metrics=['accuracy'])
Вывод:
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense (Dense) (None, 128) 100480
_________________________________________________________________
dense_1 (Dense) (None, 10) 1290
=================================================================
Total params: 101,770
Trainable params: 101,770
Non-trainable params: 0
_________________________________________________________________
Для обучения нейронной сети, выполним этот код.
model.fit(X_train, y_train, epochs=20, batch_size=128)
Вывод:
Train on 45000 samples
Epoch 1/20
45000/45000 [==============================] - 2s 54us/sample - loss: 1.3391 - accuracy: 0.6710
Epoch 2/20
45000/45000 [==============================] - 2s 39us/sample - loss: 0.6489 - accuracy: 0.8454
...
Epoch 20/20
45000/45000 [==============================] - 2s 40us/sample - loss: 0.2584 - accuracy: 0.9279
Проверяем точность на тренировочных данных.
model.evaluate(X_test, y_test)
Вывод:
[0.2567395991722743, 0.9264]
Посмотрим результаты
Вот вы и натренировали нейронную сеть для предсказания рукописных цифры с точностью выше 90%. Проверим ее с помощью изображения из тестового набора.
Возьмем случайное изображение — картинку с индексом 1010. Берем предсказанную метку (в данном случае — 4, потому что на пятой позиции стоит цифра 1)
y_test[1010]
Вывод:
array([0., 0., 0., 0., 1., 0., 0., 0., 0., 0.])
Построим изображения соответствующей картинки
plot_image(X_test[1010])
Понимание вывода активационного слоя softmax
Пропустим цифру через нейронную сеть и посмотрим, какой вывод она предскажет.
Вводные данные:
predicted_results = model.predict(X_test[1010].reshape((1, -1)))
Вывод слоя softmax — это распределение вероятностей для каждого вывода. В этом случае их может быть 10 (цифры от 0 до 9). Но ожидается, что каждое изображение будет соответствовать лишь одному.
Поскольку это распределение вероятностей, их сумма приблизительно равна 1 (единице).
predicted_results.sum()
1.0000001
Чтение вывода слоя softmax для конкретной цифры
Как можно видеть дальше, 5-ой индекс действительно близок к 1 (0,99), а это значит, что он с большой долей вероятности является
4… а это так и есть!
predicted_results
array([[1.2202066e-06, 3.4432333e-08, 3.5151488e-06, 1.2011528e-06, 9.9889344e-01, 3.5855610e-05, 1.6140550e-05, 7.6822333e-05, 1.0446112e-04, 8.6736667e-04]], dtype=float32)
Просмотр матрицы ошибок
predicted_outputs = np.argmax(model.predict(X_test), axis=1)
expected_outputs = np.argmax(y_test, axis=1)
predicted_confusion_matrix = confusion_matrix(expected_outputs, predicted_outputs)
predicted_confusion_matrix
array([[1402, 0, 4, 3, 1, 6, 20, 2, 21, 2],
[ 1, 1684, 9, 5, 4, 9, 1, 3, 9, 3],
[ 13, 8, 1280, 9, 19, 5, 12, 15, 17, 8],
[ 6, 8, 37, 1404, 1, 53, 3, 17, 33, 15],
[ 4, 7, 8, 0, 1345, 1, 18, 3, 8, 54],
[ 17, 8, 9, 31, 25, 1157, 25, 3, 24, 12],
[ 9, 6, 10, 0, 10, 12, 1431, 0, 6, 1],
[ 3, 11, 17, 4, 23, 2, 1, 1484, 5, 40],
[ 11, 16, 24, 40, 9, 25, 13, 3, 1348, 25],
[ 5, 5, 6, 16, 31, 6, 0, 43, 7, 1381]],
dtype=int64)
Визуализируем данные
# это код из https://scikit-learn.org/stable/auto_examples/model_selection/plot_confusion_matrix.html
def plot_confusion_matrix(cm, classes,
title='Confusion matrix',
cmap=plt.cm.Blues):
"""
This function prints and plots the confusion matrix.
Normalization can be applied by setting `normalize=True`.
"""
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title)
plt.colorbar()
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks, classes, rotation=45)
plt.yticks(tick_marks, classes)
fmt = 'd'
thresh = cm.max() / 2.
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, format(cm[i, j], fmt),
horizontalalignment="center",
color="white" if cm[i, j] > thresh else "black")
plt.ylabel('True label')
plt.xlabel('Predicted label')
plt.tight_layout()
# Compute confusion matrix
class_names = [str(idx) for idx in range(10)]
cnf_matrix = confusion_matrix(expected_outputs, predicted_outputs)
np.set_printoptions(precision=2)
# Plot non-normalized confusion matrix
plt.figure()
plot_confusion_matrix(cnf_matrix, classes=class_names,
title='Confusion matrix, without normalization')
plt.show()
Выводы
В течение этого руководства вы должны были разобраться с основными концепциями, которые составляют основу машинного обучения, а также научиться:
- Кодировать и декодировать изображения в наборе данных MNIST
- Кодировать категориальные значения с помощью “one-hot encoding”
- Определять нейронную сеть с двумя скрытыми слоями, а также слой вывода, использующий функцию активации softmax
- Изучать результаты вывода функции активации softmax
- Строить матрицу ошибок классификатора
Библиотеки Sci-Kit Learn и Keras значительно понизили порог входа в машинное обучение — так же, как Python снизил порог знакомства с программированием. Однако потребуются годы (или десятилетия), чтобы достичь экспертного уровня!
Программисты, обладающие навыками машинного обучения, очень востребованы. С помощью упомянутых библиотек и вводных материалов о практических аспектах машинного обучения у всех должна быть возможность познакомиться с этой областью знаний. Даже если теоретических знаний о модели, библиотеке или фреймворке нет.
Затем навыки нужно использовать на практике, разрабатывая более умные продукты, что сделает потребителей более вовлеченными.
Попробуйте сами
Вот что вы можете попробовать сделать сами, чтобы углубиться в мир машинного обучения с Python:
- Поэкспериментируйте с количеством нейронов в скрытом слое. Сможете ли вы увеличить точность?
- Попробуйте добавить больше слоев. Тренируется ли сеть от этого медленнее? Понимаете ли вы, почему?
- Попробуйте RandomForestClassifier (нужна библиотека scikit-learn) вместо нейронной сети. Увеличилась ли точность?