Как пишется математический диктант

МАТЕМАТИЧЕСКИЕ ДИКТАНТЫ НА УРОКАХ МАТЕМАТИКИ

В НАЧАЛЬНОЙ ШКОЛЕ

Математический диктант — хорошо известное средство обратной связи между учащимися и учителем. Это одна из многих оправдавших себя форм контроля знаний учеников. Выполняя задания, дети становятся более организованными и сосредоточенными. Проведение математического диктанта на этапе устного счета способствует не только развитию навыков вычисления, но и повышению их математической культуры, обогащению математического языка

Если диктанты проводятся систематически, учащиеся приучаются воспринимать задания на слух. Ценность таких навыков неоспорима — она приводит к умению слушать.

Необходимо следовать определенной методике проведения математического диктанта. Текст сначала прочитывается в целом, чтобы учащиеся знали, что от них требуется. Темп чтения определяется по темпу работы среднего ученика. Учитель выбирает такого ученика в классе, начинает читать следующее задание , когда данный ученик справился с предыдущим заданием. Необходимо следить за всем классом, реагировать на все неизбежные сбои темпа, на вопросы учащихся типа: «повторите, я не успел». Следует приучить учащихся пользоваться черновиками, где они могут делать пометки, записи в ходе диктовки.

Эффективность устного счета зависит не только от правильного определения объема и содержания этих занятий, но и от их организации: правильной постановки заданий и опроса, рационального проведения учета знаний и навыков учащихся, правильного чередования устных и письменных вычислений. Чаще всего задания предлагаются устно. Такая форма организации занятий является наиболее ценной, так как развиваются внимание и память учащихся, а главное, они подготавливаются к «жизненному» счету, где часто приходится выполнять действия над числами, воспринимаемыми на слух. Однако эта форма требует большого умственного напряжения, а поэтому сравнительно быстро утомляет детей, особенно тех, у кого преобладает зрительная память.

Наблюдающееся в школьной практике применение только этой формы занятий ведет к тому, что в устном счете участвуют не все дети. Особенно много бывает пассивных учащихся, когда диктуемые упражнения содержат большие числа или когда подряд дается много заданий на слух. Во избежание этого необходимо чисто слуховые упражнения перемежать с упражнениями на зрительное восприятие.

Основное назначение математических диктантов, помочь учителю эффективно тренировать устойчивость внимания детей, оперативную память, умение сосредоточиваться. Исходя из этих целей в диктантах даны следующие группы заданий:

• операционные, в которых нужно вычислять, решать задачи, выполнять преобразования и т.п., получив информацию на слух;
• логические, в которых требуется оценить истинность высказывания, для чего необходимо быть внимательным и сосредоточенным, уметь слушать, слышать и анализировать данные;
• направленные на усвоение математической терминологии.

Предложенные задания обеспечивают содержательным учебным материалом этап устной работы в начале урока математики, а также этап подведения итогов в конце урока. Развитию грамотной математической речи способствует наличие в каждом диктанте образцов чтения математических выражений.

Введение в математический диктант элементов игры, нестандартных заданий помогает детям, интересующимся математикой, поддерживать и развивать интерес к ней, а ребятам, у которых математика вызывает затруднения, — понять и полюбить ее.

Проведение диктанта можно организовать так:

1. Учитель читает вслух задания диктанта из одного варианта. Учащиеся на листочках или в тетрадях записывают ответы. Сразу же (либо в конце урока) следует показать верные ответы, обсудить решения отдельных заданий.
2. Прочитывать вслух задания диктантов могут отдельные учащиеся по указанию учителя. Это особенно полезно детям с недостаточной техникой чтения, а также тем, у кого преобладает зрительное восприятие.
3. Полезно время от времени в классе давать всем ученикам тексты диктантов для самостоятельной работы с ними (записав текст диктанта и на доске). Это важно для запоминания правописания математических терминов.
4. Математические диктанты можно давать и для домашней работы под руководством родителей. Это позволит каждому ученику дополнительно спокойно потренироваться в чтении математических текстов, не спеша разобраться в отдельных задачах, проверить свои знания.

Учителю читать диктант детям достаточно один раз. Это заставляет учеников быть предельно внимательными и собранными. Все вычисления и преобразования ученики выполняют только устно.

Математический диктант — одна из альтернативных форм контроля знаний, позволяющая участвовать всем учащимся сразу, а не нескольким, как при традиционном опросе.

Очень важно организовать проверку диктантов. Существует несколько видов проверки. Это запись правильных ответов на листочках с последующей сдачей их учителю на проверку, запись правильных ответов на доске, когда дети сверяют ответы со своими, взаимопроверка с соседом по парте и другие варианты, подходящие тому или иному составу учащихся. Иногда можно предложить учащимся задание на дом : составить текст математического диктанта. Оценки за работу выставляются с учетом числа верно решенных заданий. Если в диктанте 6 (или заданий, оценки могут быть такими:

Тема. «Числа от 1 до 10. Сложение и вычитание».

Цели. Проверить умение воспроизводить последовательность чисел от 1 до 10 и соотносить их с соответствующей группой предметов; сравнивать числа в пределах 10, читать простейшие математические записи вида 1 + 1 = 2 и др.; соотносить эти записи с конкретной иллюстрацией (рисунком); выполнять табличное сложение в пределах 10; представлять числа первого десятка ввиде суммы двух слагаемых; решать логические и текстовые задачи в одно действие.

Диктант 1

1. Запишите цифрами числа: 1, 5, 7.
2. Мальчик поймал 2 рыбок и выпустил их в ведро. Потом он поймал еще 3 рыбок. Нарисуйте столько рыбок, сколько всего рыбок стало в ведре.
3. В семье 4 детей: сестер столько же, сколько братьев. Сколько в семье сестер?
4. Запишите числа от 1 до 6.
5. Запишите числа от 9 до 4.
6. Заштрихуйте прямоугольник снизу вверх вертикальными линиями (прямоугольник дан на листочке).

Диктант 2

1. Назовите число, которое следует за числом 9; за числом 5.
2. К задуманному числу прибавили 1 и получили 7. Какое число задумали?
3. Какие числа пропущены, если сумма в каждом столбце равна 8?
4. Дорисуйте фигуры, чтобы количество элементов во множествах было равно.
5. У старика Хоттабыча борода длиннее, чем у доктора Айболита, но короче, чем у Карабаса Барабаса. Чья борода самая длинная?
6. Увеличьте: 9 на 1; 4 на 2; 7 на 1; 6 на 2.

Диктант 3

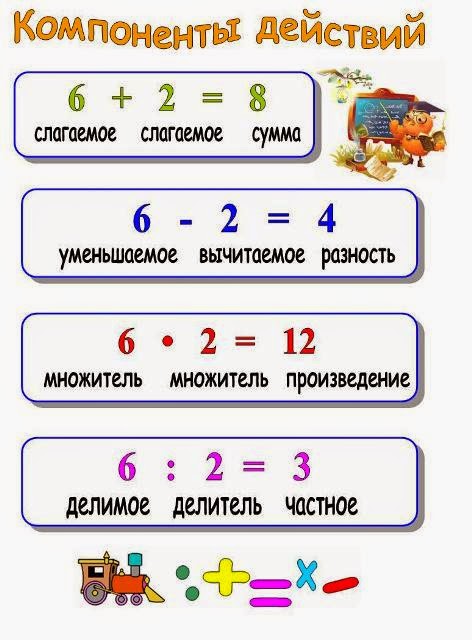
1. Первое слагаемое равно 4, а второе слагаемое равно 2. Найдите значение суммы.
2. Уменьшаемое равно 5, вычитаемое равно 3. Найдите значение разности.
3. Увеличьте 7 на 2.
4. Уменьшите 8 на 3.
5. Среди чисел каждой пары найдите то число, которое больше, и обведите его в ряду чисел красным карандашом: 9 и 8; 5иЗ; 1 и 4.
6. Найдите лишнюю по форме фигуру.
7. Соломинка выше Пузыря, а Лапоть ниже Пузыря. Кто выше: Лапоть или Соломинка?
8. Графический диктант.

Тема. «Числа от 11 до 20. Сложение и вычитание»

Цели. Проверить умение читать и записывать числа от 0 до 20; выполнять табличное сложение и вычитание в пределах 20; представлять все числа от 2 до 20 в виде суммы двух слагаемых; решать текстовые и логические задачи в одно действие.

Диктант 1

1. Запишите число, которое предшествует числу 12, 13…
2. Увеличьте 10 на 1.
3. Уменьшите 19 на 1.
4. Какое число меньше 15 на 1?
5. На сколько 12 больше 7?
6. Первое слагаемое 7, второе 4. Найдите сумму.
7. Сколько надо прибавить к 5, чтобы получить 12?
8. Чему равна сумма, если первое слагаемое 6, а второе 7?
9. В гараже было 5 машин, приехало еще 3 машины. Сколько машин стало в гараже?

Диктант 2

1.10- это 7 и еще сколько?

1. От какого числа надо отнять 5, чтобы получилось 7?
2. Найдите значение разности чисел 15 и 9.
3. Увеличьте 7 на 5.
4. Уменьшаемое 12, вычитаемое 8. Найдите разность.
5. У брата 5 тетрадей, у сестры столько же. Сколько тетрадей у брата и сестры вместе?
6. Гребенчатый тритон линяет каждые 7 дней. Сколько раз пройдет линька у тритона за 14 дней.

Литература:

1. Истомина Н.Б., Шмырева Г.Г. Дидактические карточки-задания по математике.— М. Астрель. 1979.
2. Гейдман Б.П. Математика. — M.: Изд-во Московского университета, 1999.
3. Волкова С.И., Столярова Н.Н. Тетрадь с математическими заданиями. — M.: Просвящение, 1993.
4. Голубь В.Т.Математические диктанты 2 класс. — Воронеж. 2011.

Здравствуйте, уважаемые родители моих Буквоежек и сами Буквоежки!

Сегодня я хочу поговорить с вами о том, что такое математический диктант.

 Вы, ребята, пишете такие диктанты с 1-ого класса, но сейчас, во 2-ом классе, появилось много вопросов у ваших родителей — что это за зверь такой и почему некоторым ребятам никак его не укротить…

Немного теории…

«После прохождения определённого объема учебного материала, перед учителем встает вопрос о проверке качества усвоения материала учениками. Провести опрос всех учеников — задача непосильная и нереальная как по времени, так и физически.
Если же провести выборочный опрос нескольких учеников, то обычно остальные ученики слушают их не внимательно. Поэтому для комплексной проверки качества усвоения материала применяются контрольные работы, тесты, самостоятельные работы или математические диктанты.
В большинстве случаев, математические диктанты выполняются устно. И в этом — их особенность и достоинство. При выполнении арифметических операций в устном виде, ученики закрепляют ранее полученные навыки и выполняют математические действия более осмысленно, а не механически. При регулярном выполнении устных вычислений тренируются внимание, сосредоточенность, смекалка».

Итак, как проходит такой диктант в классе.
Во-первых, всегда в начале урока. Во-вторых, такой диктант мы проводим 1-2 раза в неделю (а в неделю 4 урока математики) фронтально, т.е. я задаю вопрос, спрашиваю ответ и все ребята его записывают. Или после моего озвучивания сначала записывают, а потом проговаривают правильный ответ для проверки. Или пишем весь диктант (обычно 10 примеров-заданий), а потом проверяем, зачитывая ответы. 

Диктую задание я только один раз! Дети уже привыкли, знают, что нельзя переспрашивать, надо поставить прочерк. Почему так? Потому что переспрашивание отвлекает других детей и заставляет их ошибаться.
Через какой интервал диктую, не могу сказать… Я смотрю на детей. У нас есть специальный знак (рука на локоток), который означает, что ответ записан. Могу сказать точно одно — такой вид деятельности не занимает у нас больше 7-10 минут.

Как выглядят задания?

Чему равна сумма чисел 12 и 17?
Чему равна разность чисел 19 и 4?
Первое слагаемое — 11, второе слагаемое — 4. Чему равна сумма этих двух слагаемых?
Уменьши число 17 на 5.
Увеличь число 8 на 7.
Какое число надо увеличить на 7, чтобы получить число 18?
Увеличь число 9 на 9.
Найди сумму чисел 3 и 4 и прибавь к полученной сумме 5.
Сколько получится, если к 8 прибавить 5?
От числа 19 отними сумму чисел 3 и 4.
Найди произведение чисел 7 и 3.
На сколько надо умножить 4, чтобы получилось 20?
Первый множитель — 6, второй — 3. Найди произведение.

Чтобы грамотно и без ошибок писать математические диктанты, ребенок должен не только хорошо считать, но и точно знать названия компонентов действий (плакаты висят у нас над доской, так что всегда есть возможность «подглянуть», если забыл)

Напоминаю их здесь:

Ну а если хочется быть во всеоружии при штурме такой крепости, как математический диктант, то приглашаю вас сюда — здесь я буду обновлять задания для тренировки

Желаю удачи в освоении устного счета, Буквоежки!

Большое спасибо маме Даши А., Марине Викторовне, за идею, 

как оказалось, актуального и полезного поста! 

Обращайтесь, уважаемые родители, 

о своими вопросами и пожеланиями, буду рада помочь!

Математический диктант
как форма проверки знаний

Важным и чрезвычайно тонким моментом учебно-воспитательного
процесса как для учителя, так и для ученика является контроль знаний.
Контроль — составная часть процесса обучения и обеспечивает учителю
получение информации о ходе познавательной деятельности учащихся в процессе
обучения, а ученикам — получение информации о своих успехах. Контроль
знаний имеет обучающее и воспитывающее значение, способствует более глубокому
изучению учащимися основ наук, совершенствованию их знаний и умений.

Математические диктанты — хорошо известная форма контроля
знаний. Учитель сам или с помощью звукозаписи задает вопросы, учащиеся
записывают под номерами краткие ответы на них. Как правило, ребятам трудно
воспринимать задания на слух. Но если диктанты проводить часто, то школьники
овладевают этим навыком. А ценность такого умения неоспорима. Иногда слуховому
восприятию нужно помочь. Для этого одновременно с чтением задания делаю запись
или чертеж на доске. В зависимости от подготовленности учащихся число заданий
увеличиваю или уменьшаю.

Прежде чем перейти к объяснению нового материала, целесообразно
убедиться, что предыдущая порция знаний учащимися усвоена. Традиционная
методика рекомендует в этом месте педагогического процесса организовать опрос
учащихся. Опрос, как форма проверки знаний, неэффективен, и прежде всего
потому, что для большей части учащихся ответ одноклассника у доски вовсе не
помогает повторить ранее изученное. Всякого рода уплотненные опросы, когда
одновременно готовятся до 10 учеников, лишь усугубляют дело: вызванные не
слушают ответ товарища на законном основании.

Опрос у доски обычно дополняют так называемым устным счетом.
Недостаток традиционного «устного счета» в том, что в нем участвуют не все
ученики. Альтернатива опроса и «устного счета» — математический диктант.
Отсюда — его место в учебном процессе: в начале урока, на котором
начинается изложение новой порции знаний. Отсюда — требование к его
содержанию: ответы на вопросы должны показывать, усвоено ли содержание ранее
изложенного материала. Математический диктант может заменить опрос по теме,
заданной для повторения. Его продолжительность обычно 10–15 минут.
Он представляет собой систему вопросов, связанных между собой.

Содержание заданий

Рассмотрим различные виды заданий, с которыми сталкиваются ученики
в диктантах.

1. Задания репродуктивного типа выполняются учащимися на
основе известных формул и теорем, определений, свойств тех или иных
математических объектов.

Репродуктивные задания позволяют
выработать основные умения и навыки, необходимые для изучения математики. И
хотя они мало способствуют развитию мышления учащихся, однако создают базу для
дальнейшего изучения математики и таким образом способствуют выполнению заданий
более высокого уровня сложности.

2. Реконструктивные задания указывают только на общий принцип решений (например, «решите
графически неравенство») или на соотнесение к тому или иному материалу
(например, «решите задачу составлением системы уравнений»). Выполнение таких
заданий возможно только после того, как ученик сам реконструирует их, соотнесет
с несколькими репродуктивными. К такого рода заданиям можно отнести задания на
построение графиков, задачи на составление уравнений, задания, при выполнении
которых учащимся приходится использовать несколько алгоритмов, формул, теорем
(например, «представьте в виде многочлена выражение (а – 2)x(а +
2) – (2 – а)²»).
Эти задания характерны тем, что, приступая к их выполнению, ученик должен
проанализировать возможные общие пути решения задачи, отыскать характерные
признаки объекта, использовать несколько репродуктивных задач. Отметим, что
познавательная деятельность ученика при выполнении этих заданий не выходит за
рамки воспроизведения знаний, но неизбежно сопровождается некоторым обобщением.
Реконструктивные задания — наиболее распространенный вид заданий,
используемый на всех этапах учебного процесса.

3. Более высоким уровнем воспроизводящей деятельности и
переходом ее в творческую характеризуются задания вариативного характера. При выполнении их ученику необходимо из всего арсенала
математических знаний отобрать нужные для решения данной задачи,
воспользоваться интуицией, найти выход из нестандартной ситуации. К такого рода
заданиям относятся так называемые задачи на сообразительность, задачи «с
изюминкой», многие задачи на доказательство, а также задачи, для решения
которых необходимо создание новых алгоритмов решения (например, «Вставьте
пропущенные одночлены так, чтобы получилось тождество а² + 6аb + … = (… + …)²»).

Чтобы развивать мышление учащихся, формировать у них различные
виды деятельности на всех этапах обучения математике, необходимо использовать различные
виды заданий.

Математический диктант — это один из способов организации
самостоятельной деятельности учащихся. Система математических диктантов, с
одной стороны, должна обеспечивать усвоение необходимых знаний и умений, с
другой стороны, их проверку.

Виды диктантов

Математические диктанты можно разделить на следующие виды:
проверочные, обзорные, итоговые. Каждый вид математических диктантов имеет свои
особенности, свои цели, и следовательно, требования, предъявляемые к
составлению этих работ, должны быть различны.

Проверочные диктанты предназначены
для контроля усвоения отдельного фрагмента курса в период изучения темы. При их
выполнении учитель своевременно получает информацию о том, как усваивается
тема, что позволяет ему вовремя выявить ошибки, обнаружить плохо усвоивших тот
или иной материал и в зависимости от этого строить работу по изучению данной
темы. Учащиеся же получают дополнительную практику в самостоятельном решении
задач и тем самым готовятся к контрольной работе по данной теме. Поскольку
проверочные диктанты проводятся после отработки основных умений и навыков, то в
них включаются задания не только репродуктивного характера. Основа проверочных
диктантов — задания реконструктивного характера. В то же время в
проверочные диктанты не следует включать задания сложнее тех, которые
выполнялись учащимися на уроках и дома.

В процессе изучения некоторых разделов курса учитель проводит
несколько контрольных работ, дающих представление об усвоении отдельных тем,
входящих в этот раздел. Однако после завершения изучения раздела целесообразно
проверить его усвоение в целом, для этой цели можно провести обзорный
диктант, который позволит учащимся повторить материал, систематизировать
знания, установить связи между изученными вопросами. Для этого необходимо
определить, какие основные понятия должен усвоить ученик при прохождении этого
раздела, какие умения и навыки должен приобрести, какие задания уметь
выполнять, каков уровень сложности этих заданий. При этом не должно быть
заданий, отягощенных сложными тождественными преобразованиями, трудоемкой
вычислительной работой, требующих на свое выполнение много времени. Задания
должны быть четкими, конкретными, понятными. Сюда входят вопросы по проверке
изученных определений, теорем, правил, задания на решение несложных задач и
упражнений. Основу обзорных диктантов составляют задания репродуктивного
характера. Составленный таким образом диктант дает возможность учителю
проверить усвоение узловых вопросов всего раздела.

Организация повторения является важным моментом в методике
обучения математике. Повторение ранее изученного материала в связи с его
использованием при изучении нового материала является наиболее распространенным
видом повторения. Существуют и другие виды повторения, — в частности,
обзорное и итоговое повторение темы, раздела, курса.

Завершающим моментом повторения в конце года может явиться
проведение итоговых диктантов по основным содержательным линиям изученного курса.

В них следует включать задания репродуктивного и реконструктивного
характера, которые должны проверять основные умения и навыки; задания на
повторение основных теоретических вопросов: воспроизведение определений и
свойств математических объектов.

Способы проведения диктантов

Текст диктанта может быть:

а) спроецирован на доску с помощью компьютера;

б) зачитан учителем;

в) воспроизведен с помощью звукозаписи;

г) с графической записью ответа.

При чтении заданий диктанта паузы определяются по темпу работы
среднего ученика. Наблюдения показали, что достаточна пауза, равная времени
повтора текста. Следует помнить, что математический диктант проверяет не
сообразительность учащихся, а их знания. И если учащийся при ответе на вопрос
диктанта надолго задумался, он просто не знает ответ, и долгая пауза ему не
поможет.

Методика проведения

Проведение диктанта, особенно в два варианта, требует от учителя
весьма большого напряжения: надо читать в оптимальном темпе тексты заданий;
следить за классом; реагировать на неизбежные сбои («повторите», «а у меня
ручка перестала писать» и т.п.).
К тому же учащиеся нередко не понимают, какой именно из двух вариантов в данный
момент диктуется, и в результате перепутывают задания вариантов. Подобные
трудности легко преодолеваются с помощью звукозаписей, в которых задания первого
варианта читает мужской голос, а второго — женский. Ученик не реагирует на
«чужой» голос: спокойно работает пока диктуется задание другого варианта, а как
только начинается чтение задания его варианта, немедленно включается в работу.
Использование звукозаписей дисциплинирует класс: ученик понимает, что
«бездушной машине» все равно, успел ли он подготовить все необходимое к началу
диктанта, пишет ли его ручка и т.п., и сбои становятся крайне редкими. Учителю
использование звукозаписи при проведении диктанта дает возможность наблюдать за
работой учащихся, делать необходимые и убирать уже ненужные записи и рисунки с
доски и т.д.

Диктант можно провести и так.

1) Учитель полностью зачитывает текст, а учащиеся слушают, не
делая записей.

2) Учитель читает текст по фразам, делая паузы (от одной до
четырех минут), чтобы дать учащимся возможность выполнить задание.

3) Когда все задания выполнены, учитель снова читает весь
текст с небольшими остановками (это дает учащимся возможность что-то исправить
и сделать дополнения).

4) Правильные ответы записываются на доске, и ученики
самостоятельно проверяют диктант у соседа по парте. В 5–7-х классах все работы
проверяются учителем.

Организация проверки

Обычный способ проверки, когда ответы учащихся учитель собирает и
проверяет дома, малоэффективен: ребенок жаждет узнать результаты своей работы
непосредственно после завершения, на следующий день они его интересуют уже
меньше. Поэтому организовать проверку можно, например, так. Учащиеся пишут
диктант под копирку. Первый экземпляр сдается учителю сразу после слов «диктант
окончен», а копия остается у ученика и используется для проверки правильности
выполнения работы: учитель записывает на доске правильные ответы.

Весьма важно обучить учащихся правильной проверке своих
математических диктантов. Иначе некоторые ученики просто не замечают допущенных
ошибок. Можно предложить учащимся самостоятельно оценивать результаты диктанта
по указанным критериям.

Вот возможная шкала оценок для диктантов различной длины.

После того как учащиеся научатся проверять свои математические
диктанты, учитель может вообще перестать проверять их дома. Вместо самопроверки
можно делать взаимопроверку — между двумя учениками. Можно организовать
проверку и так: ученик передает свой листок другому ученику, который писал тот
же вариант. Он сверяет ответы и ставит знаки «+», «–», «?» не только в своем листке,
но и в листке товарища, и отметки ставит в обоих листках. После завершения
проверки учитель называет фамилию ученика. Ученик называет поставленную им себе
отметку, и сразу же называет поставленную ему отметку одноклассником, который
сверял ответы на его листке. Если отметки совпадают, учитель ставит ее в
журнал. Если нет, берет диктант на перепроверку.

Но, пожалуй, самым важным в организации проверки диктанта сразу
после его завершения является то, что появляется возможность обсудить все те
вопросы, которые вызвали затруднения или особенно важны для понимания нового
материала: детей, которые только что написали математический диктант,
интересует не только отметка, но и обоснование решения. Эта работа может быть
организована, например, так. Учитель предлагает сверить ответ, полученный при
выполнении первого задания, и поднять руку всем тем, кто допустил ошибку. Если
ошибок немного и само задание не такое уж важное, учащимся предлагается сверить
свои результаты по второму заданию. Если же оказалось, что решение задания
необходимо разъяснить, кто-либо из учеников или учитель дают необходимые
пояснения.
В случае необходимости учащимся по ходу проверки предлагается выполнить
аналогичное задание. При сверке ответов эффективен следующий прием. Учитель
показывает верный ответ и просит сверить с ним свои ответы. О совпадении или не
совпадении ответов должны одновременно сигнализировать все ученики. Это можно
сделать, например, с помощью карточек разных цветов; совпадение —
поднимается зеленая карточка, не совпадение — красная. Учитель видит
одновременно ответы всех учащихся и может сказать каждому, верен ли его ответ.
Разница между традиционным поднятие руки и описанным голосованием огромная: там
отвечает лишь вызванный, здесь — все. Вместо сигнальных карточек можно
использовать голосование по следующим правилам: в случае согласия поднимают
правую руку, в случае не согласия — левую. А чтобы учащиеся не забыли и не
перепутали, на доске надо написать слева слово «нет», справа — слово «да».
Поднятые руки, как и цветные карточки, позволяют учителю немедленно узнать,
правильно или не правильно каждый ученик выполнил задание.

Заключение

Процесс обучения — процесс двусторонний; для успеха обучения
требуется не только высокое качество работы учителя, но и активная деятельность
учащихся, их желание овладеть передаваемыми учителем знаниями, их интерес к
обучению, сосредоточенная и вдумчивая работа под руководством учителя. Все эти
реакции у учащихся должен вызвать к действию учитель, опираясь на свой
авторитет, на контакт с учащимися, на свою увлеченность предметом, профессией,
любовь и благожелательное отношение к детям.

Практика показывает, что реальный учебный процесс не всегда
удается организовать достаточно хорошо. Систематически применяя на своих уроках
математические диктанты наряду с другими формами проверки знаний, убеждаешься в
том, что они являются эффективным средством активизации учебной деятельности.
Но важно подчеркнуть, что в силу специфики математических диктантов
(воспринимаемые на слух вопросы; лаконичные ответы) их педагогические
возможности ограниченны. С их помощью, как правило, можно проверить, усвоили ли
учащиеся обязательный минимум знаний, но нельзя организовать углубленную
проверку. Поэтому было бы ошибкой противопоставлять диктанты другим формам
контроля. Одно и то же задание может быть как в диктанте, так и в
самостоятельной работе, но эти задания будут иметь разную дидактическую
функцию.
В самостоятельной работе от ученика требуется фиксирование хода работы, что
делает подконтрольным поиск результата. В математическом диктанте контроль
может вестись лишь по конечному результату. Надеюсь, что мой опыт заинтересует
коллег-математиков, будет полезен при обучении учащихся.

Статья подготовлена при поддержке информационно-образовательного
портала «edustudio.ru». Если Вы решили приобрести или углубить свои познания в
математике, то оптимальным решением станет обратиться в
информационно-образовательный портал «edustudio.ru». Перейдя по ссылке: «решение задач», вы сможете, не отходя от экрана монитора, посмотреть решенные
примеры, а также задать интересующий вопрос. Более подробную информацию вы
сможете найти на сайте www.edustudio.ru.

Рекомендуемая литература

1. Арутюнян Е.Б., Волович М.Б., Глазков Ю.А.,
Левитас Г.Г. Математические
диктанты для 5–9 классов. — М.: Просвещение, 1991.
2. Афанасьева Т.Л., Тапилина Л.А. Геометрия. 9 класс. (Пособие для учителя к
учебнику Л.С. Атанасяна, и др. «Геометрия. 7–9 классы»). — Волгоград:
Учитель, 2007.
3. Барышникова Н.В. Математика. 5–11 классы. Нестандартные
уроки. — Волгоград: Учитель, 2007.
4. Груденов Я.И. Совершенствование методики работы учителя
математики. — М.: Просвещение, 1990.
5. Ершова А.П., Голобородько В.В. Устные проверочные и зачетные работы по
геометрии для 7– 9 классов. — М.: Илекса, 2004.
6. Есипов Б.П. Самостоятельная работа учащихся на
уроках. — М., 1961.
7. Зив Б.Г., Алтынов П.И. Алгебра и начала анализа. Геометрия. 10–11
классы. Учебно-методическое пособие. — М., 1999.
8. Лебедев П.М. Понятие познавательной активности учащихся
и пути ее измерения//Радянська школа, 1970, № 9.
9. Левитас Г.Г. Диктанты по алгебре. 7– 11 классы.
Дидактические материалы. — М.: Илекса, 2005.
10. Левитас Г.Г. Математические диктанты. Геометрия. 7–11
классы. Дидактические материалы. — М.: Илекса, 2006.
11. Леонтьева М.Р., Суворова С.Б. Упражнения в обучении алгебре. — М.:
Просвещение,1985.
12. Манвелов С.Г. Конструирование современного урока
математики. — М.: Просвещение, 2002.
13. Ремчукова И.Б. Математика. 5–8 классы. Игровые технологии
на уроках. — Волгоград: Учитель, 2007.
14. Терский С.Б. Игра. Творчество. Жизнь. — М., 1966.

Математический диктант как техника формирующего оценивания

Автор: Гаврилова Татьяна Викторовна

Организация: ГБОУ СОШ №367 Фрунзенского района Санкт-Петербурга

Населенный пункт: г. Санкт-Петербург

Математические диктанты прочно вошли в практику работы учителей и приобрели особую популярность с 70-80 годы XX века, когда сотрудниками лаборатории математики Научно-исследовательского института школьного оборудования и технических средств обучения Академии педагогических наук СССР была разработана технология учебных циклов и проведено исследование эффективности применения математических диктантов. (далее — МД)

В данной статье описывается опыт использования математических диктантов на уровне среднего общего образования.

Применение математических диктантов(далее — МД), в отличие от фронтального устного опроса, позволяет включить в деятельность всех обучающихся и оперативно получить информацию об уровне усвоения учебного материала как отдельными учениками, так и классом в целом.

Ученики знают, что практически каждый урок начинается с диктанта или устной самостоятельной работы. Таким образом, каждый ученик с первых минут урока включается в целенаправленную учебную деятельность, концентрируется его внимание, экономится время на организационном этапе урока.

В зависимости от задач урока, математический диктант проводится с целью текущего контроля, диагностики затруднений, актуализации или систематизации знаний учащихся, отработки навыков построения изображений, обеспечения готовности к изучению новой темы.

Диктант содержит 5-10 вопросов, не требующих подробной записи решения. Ученики выполняют задание устно и записывают только ответ или номер выбранного высказывания. Время на выполнения работы определяется ее содержанием и не превышает 15 минут. По необходимости вопросы учителя сопровождаются визуальной информацией: эскизом графика функции, рисунком, изображением геометрических фигур. Для этого используется мультимедийный комплекс.

Результаты диктанта тут же обсуждаются, даются правильные ответы. Это позволяет каждому ученику осознать свои пробелы в знаниях, а учителю оперативно получить обратную связь, скорректировать ход урока и спланировать дальнейшее изучение предмета.

В соответствии с требованиями к уровню математической подготовки, в X-XI классах задания можно разделить на следующие группы:

Если математический диктант проводится с целью контроля сформированности предметных результатов, то оценивание проводится по пятибалльной шкале. В этом случае, 3/5 (60%) вопросов должны проверять опорные знания учащихся , а 2/5 (40%) умение применять опорные знания в новых ситуациях, т. е. задания повышенного уровня. Тогда применяются такие критерии оценивания:

отметка «3» — правильно выполнены задания базового уровня;

отметка «4»-правильно выполнено 4/5 от общего числа заданий МД или (от 60 до 80%);

отметка «3» правильно выполнено все задания МД, или более 4/5 от общего числа заданий, или более 80%.

Данные критерии оценивания принимаются (в обсуждении с учащимися) на первых уроках в X классе. Для развития у учеников навыка адекватной самооценки результатов учебной деятельности важно от принятых критериев не отступать.

Если МД проверяет готовность к изучению нового материала, то целесообразно отказаться от пятибалльной шкалы оценивания. Ученики фиксируют в тетрадях вопросы, на которые не смогли дать правильный ответ. В ходе урока выделяется время на коррекцию знаний (5-10 мин. в зависимости от числа учеников, не справившихся с базовой частью МД). Организуется работа по коррекции учебных дефицитов. Для этого можно использовать учебник или организовать работу в парах, когда более успешный ученик помогает товарищу, не выполнившему задания базовой части. Проводить коррекцию на повышенном уровне в общеобразовательном классе не целесообразно.

Учитель может использовать накопительную систему оценивания, учитывая индивидуальное продвижение ученика внутри одной темы. При этом, отметка не должна выставляться как средний балл, в журнале фиксируется та отметка, которая соответствует результатам ученика на момент окончания изучения темы. Такой подход соответствует принципам формирующего оценивания, дает ученикам право допустить ошибку и организовать свою учебную деятельность по её исправлению.

Описанный опыт применения в образовательном процессе предметных диктантов может быть использован учителями любых предметов на любом уровне образования. Данная педагогическая техника «экономична», не требует специальных условий и ресурсов, соответствует требованиям федеральных государственных образовательных стандартов,.

Системное использование на уроках математических диктантов обеспечивает достижение планируемых результатов освоения основной образовательной программы (в особенности регулятивных универсальных учебных действий), а также эффективно в качестве инструмента формирующего оценивания как предметных, так и метапредметных результатов.

Список литературы::

Примерная основная образовательная программа среднего общего образования. http://rulaws.ru/acts/Primernaya-osnovnaya-obrazovatelnaya-programma-srednego-obschego-obrazovaniya/

Землянская Е.Н. Формирующее оценивание (оценка для обучения) образовательных достижений обучающихся [Электронный ресурс] // Современная зарубежная психология. 2016. Том 5. No 3. С. 50—58. doi: 10.17759/jmfp.2015050306

Пинская М.А. Формирующее оценивание: оценивание в классе Текст.:учеб. пособие / М.А. Пинская. – М.: Логос, 2010. – 264 с.

Левитас, Г.Г. Технология учебных циклов, или как улучшить классно -урочную систему обучения Текст. : практическое пособие / Г.Г.Левитас. -М.:АРКТИ, 2006. -72 с.

Электронная библиотека изданий программы «МГУ-школе».Электронный ресурс. Левитас Г.Г. Технология учебных циклов // http://lib.teacher.msu.ru/pub/3048

Приложение

Диктант по теме «Степень с действительным показателем»

Диктант по теме «Расстояния в пространстве»

По каждому вопросу необходимо написать определение, сделать рисунок и краткую (символическую) запись

Опубликовано: 14.10.2020

МЕТОДИЧЕСКАЯ РАЗРАБОТКА

«Рекомендации по проведению и проверки математического диктанта»

 Зачем нужны математические диктанты?

Математические диктанты – одна из форма контроля знаний. Но употребляются они всё же редко, так как учащимся трудно воспринимать задания на слух. Одной из важнейших задач в обучении является формирование у детей умения получать информацию на слух, запоминать на слух, обрабатывать и преобразовывать информацию. Из имеющихся в нашем распоряжении органов чувств, воспринимающих информацию, слуховой орган занимает второе место после зрительного, поэтому развивать его возможности у детей крайне важно. Использование математических диктантов помогает в решении этих задач. 
Если диктанты проводить часто , то школьники приучаются воспринимать задания на слух. А ценность такого умения очень важна в жизни . Оно приводит к умению слушать собеседника , телепередачу , слушать лекцию.

Математические диктанты проводятся со следующими целями.

Прежде всего, они помогают контролировать знания, умения и навыки учащихся. Проанализировав диктанты, учитель получает достаточно подробную информацию об уровне усвоения пройденного как отдельными учащимися, так и классом в целом. Это позволяет оперативно устранять пробелы в подготовке учащихся.

Однако ещё более важно то, что математические диктанты играют обучающую роль. Выслушав фразу диктанта, учащиеся выполняют определенную работу – записывают алгебраическое выражение выполняют указанное построение. При этом требуется не только воспроизвести заученную формулировку, а творчески подойти к заданию.

Диктанты способствуют и развитию навыков логического мышления, и выработке умения работать с чертежными инструментами. 
Известная не шаблонность постановки задачи и ограниченность времени на выполнение задания дисциплинируют учащихся, приучают к собранности, сосредоточенности, целеустремленности. 
Проведение математических диктантов способствует и повышению общей грамотности учащихся.В результате систематического использования этой формы работы резко уменьшается количество ошибок в написании математических терминов.

 Достоинства и недостатки математических диктантов .

недостатки математических диктантов .

• не по любой теме можно провести диктант,

• не все учащиеся способны хорошо воспринимать задания на слух ,

• с их помощью можно проверить, усвоили ли учащиеся обязательный минимум знаний, но нельзя организовать углубленную проверку.

Но наряду с недостатками можно отметить и достоинства:

• математические диктанты развивают умение воспринимать задания на слух, а это ведет к умению слушать лекцию и слушать вообще,

• это альтернатива устного счета, который охватывает не всех учеников,

• ответы на вопросы диктанта показывают, усвоено ли основное содержание ранее изложенного материала.

Для диктантов лучше использовать листы бумаги (бланки ответов). Можно использовать при проведении диктанта два бланка ответов для того, чтобы ученик мог один бланк сдать учителю, а второй использовать для проверки правильности выполнения работы. Если есть закрытые доски, то можно, либо написать ответы заранее, либо вызвать два ученика к доске и их ответы проверить вместе с классом. Проверка сразу на уроке даёт возможность ещё раз закрепить изученный материал.

Во время проверки напротив правильного ответа ученик ставит «+», напротив ошибочного – «минус», напротив ответа с недочетом —  «плюс, минус». Можно при проверке обменяться работами с соседом по парте.

Ó÷èòåëü äîëæåí äèêòîâàòü âîïðîñû ÷åòêî, ãðîìêî, äåëàòü äîñòàòî÷íûå ïàóçû, ÷òîáû äåòè óñïåëè çàïèñàòü îòâåòû. Âîïðîñ íåîáõîäèìî ÷èòàòü ïî äâà ðàçà, êàæäûé âàðèàíò ïî î÷åðåäè. ×òîáû äåòè íå ïóòàëè âàðèàíòû, ìîæíî âûïîëíèòü àóäèîçàïèñü òåêñòà äèêòàíòà, ïåðâûé âàðèàíò – æåíñêèì ãîëîñîì, âòîðîé – ìóæñêèì. Ó÷åíèê ñêîðî âîîáùå ïåðåñòà¸ò ðåàãèðîâàòü íà “íå ñâîé” ãîëîñ: ñïîêîéíî ðàáîòàåò, ïîêà äèêòóåòñÿ çàäàíèå äðóãîãî âàðèàíòà, è íåìåäëåííî âêëþ÷àåòñÿ â ðàáîòó, êàê òîëüêî íà÷èíàåòñÿ ÷òåíèå çàäàíèÿ åãî âàðèàíòà. Èñïîëüçîâàíèå çâóêîçàïèñåé ÷ðåçâû÷àéíî äèñöèïëèíèðóåò êëàññ: ó÷åíèê ïîíèìàåò, ÷òî ìàøèíå âñ¸ ðàâíî, óñïåë ëè îí. Ïîýòîìó ñáîè ñòàíîâÿòñÿ ðåäêèìè. Åñëè íåò òàêîé âîçìîæíîñòè, ìîæíî ñäåëàòü ñëåäóþùåå: êîãäà ó÷èòåëü äèêòóåò âîïðîñû ïåðâîãî âàðèàíòà, îí ñòàíîâèòñÿ ïåðåä ó÷àùèìèñÿ, ñèäÿùèì íà ïåðâîé ïàðòå íà ïåðâîì âàðèàíòå, à êîãäà äèêòóåò âîïðîñû âòîðîãî âàðèàíòà, îí ñòàíîâèòñÿ ïåðåä ó÷àùèìèñÿ, ñèäÿùèìè íà ïåðâîé ïàðòå íà âòîðîì âàðèàíòå, èëè êîãäà ó÷èòåëü äèêòóåò âîïðîñû ïåðâîãî âàðèàíòà, îí äåðæèò â ðóêàõ ëèñò ñ öèôðîé 1, à êîãäà äèêòóåò âîïðîñû âòîðîãî âàðèàíòà, îí äåðæèò â ðóêàõ ëèñò ñ öèôðîé 2 .

Учитель может – исходя из особенностей учащихся класса, может использовать свои подходы к оцениванию результатов диктанта. Иногда вопросы диктанта по значимости и содержанию можно разделить на “лёгкие” и “трудные”. В этом случае есть смысл каждый вопрос оценить в баллах (например, от 1 до 3 баллов), тогда итоговая оценка выставляется по сумме баллов. 

Если Вы в своей работе не применяете математические диктанты, значит для этого есть причины: Много времени тратится на подготовительную работу. Проведение диктанта требует от учителя весьма большого напряжения: надо читать в оптимальном темпе тексты заданий, следить за классом, реагировать на практически неизбежные сбои.

ПРИЛОЖЕНИЕ

5 класс.

Диктант по теме: «Признаки делимости на 9 и на3.»

1. Закончите предложение: «Число делится на 9 ( 3 ), если сумма цифр числа…»

2. Пользуясь признаками делимости на 3, определите, делятся ли числа 3213, 78213, 43552, 117 ( 2511, 65031, 45083 450) на 3? 

3. Пользуясь признаками делимости на 9 , определите, делятся ли числа 3213, 78213, 43552, 117( 2511, 65031, 45083 450) на 9? 

4. 4. Какие цифры можно подставить вместо звездочки в запись числа   641 * 2   , чтобы
   это число делилось на девять (три)? 

5. Какие цифры можно подставить вместо звездочки в запись числа   973 *   , чтобы это число не было кратно трем (девяти)?

6. Напишите наименьшее четырехзначное число, чтобы это число делилось на девять (три)? 

7. Напишите наибольшее трехзначное число, чтобы это число не делилось на девять (три)? 

Диктант по теме: «Процент.»

1. Закончите предложение: «Один процент – это…» (« Процентом называется…»).

2. Запишите в виде десятичной дроби 32% (25%).

3. Запишите в процентах десятичную дробь 0,25 (0,32).

4. Сколько процентов число 1 составляет от числа 5 ( 4 от 20)?

5. Как называется один процент центнера ( 0,1% от тонны)?

6. Найдите 25% от 8 км ( 40% от 15 км).

7. Найдите 15%от 25 руб. (30% от 50руб.)

8. В коробке 3 красных и 67 синих карандашей. Сколько % от всех

карандашей составляют синие (красные) карандаши?

Диктант по теме: «Прямоугольный параллелепипед.»

1. Закончите предложение: «У  прямоугольного параллелепипеда противоположные грани — …» («Куб — это прямоугольный параллелепипед, …»).

2. Сколько проволоки потребуется для изготовления каркаса куба с ребром 6см ( 8см)?

3. Сколько в прямоугольном параллелепипеде вершин (ребер)?

4. Может ли только одна грань прямоугольного параллелепипеда являться квадратом (не являться квадратом) ?

5. Сколько в прямоугольном параллелепипеде граней(вершин)?

6. Используя размеры прямоугольного параллелепипеда вычислите площадь поверхности:

а = 2 м а = 6 см

в = 5 м в = 5 см

с = 4 м с = 3 см

7. Сколько в прямоугольном параллелепипеде ребер (граней)?

6 класс.

Диктант по теме: «Основное свойство пропорций.»

1. Закончите предложение: «Равенство двух отношений называют…. («Если пропорция верна, то произведение ее крайних членов равно …»).

2. Êàê íàçûâàþòñÿ ÷èñëà õ è ó (à è â ) â ïðîïîðöèè õ:à=â:ó?

3. ×èñëî âîñåìíàäöàòü òàê îòíîñèòñÿ ê ÷åòûðåì, êàê äâàäöàòü ñåìü îòíîñèòñÿ ê øåñòè. Çàïèøèòå ïðîïîðöèè

4. Íàéòè íåèçâåñòíûé ÷ëåí ïðîïîðöèè: õ:14=36:7 (õ:12=36:18 ).

5. На участке дороги плиты длинной 6 м заменили новыми длиной 8 м. Сколько нужно новых плит для замены 240 старых?

6. Âåðíà ëè ïðîïîðöèÿ:    ( ). 

7. Три ученика пропололи грядку за 4ч. За сколько часов выполнят 
работу два (четыре) ученика?

Диктант по теме: «Умножение.»

1. Óìíîæüòå 3 íà -4 (-5 íà 0).

2. Óìíîæüòå -3 íà 0 (-8 íà -3).

3. Ðåøèòå óðàâíåíèå: õ / 6 = ( -3 ), õ / ( — 4) = 8

4. Ïðîäîëæèòå ïðåäëîæåíèå: «×òîáû óìíîæèòü îòðèöàòåëüíîå ÷èñëî íà ïîëîæèòåëüíîå, íàäî…» («×òîáû ïåðåìíîæèòü äâà îòðèöàòåëüíûõ ÷èñëà, íàäî…»).

5. Âåðíî ëè âûñêàçûâàíèå (îòâåòüòå «äà» èëè «íåò»): «Ïðîèçâåäåíèå äâóõ îòðèöàòåëüíûõ ÷èñåë — ïîëîæèòåëüíîå ÷èñëî» («Ïðîèçâåäåíèå äâóõ öåëûõ ÷èñåë íå ìîæåò áûòü ìåíüøå êàæäîãî èç ìíîæèòåëåé»).

6. Ðåøèòå óðàâíåíèå: ó ( ó – 4) = 0, õ ( õ +5) = 0

7. Âû÷èñëèòå çíà÷åíèå âûðàæåíèÿ ó*(- 16) ïðè ó=3 (11õ ïðè õ= -5 )

7 класс. Геометрия.

Диктант по теме: «Вертикальные углы.»

1. Продолжите предложение: «Два угла называются вертикальными, если…»( «Если стороны одного угла являются продолжением сторон другого угла, то такие углы…» )

2. Чему равен угол, вертикальный углу в 47⁰( 123⁰ ) ?

3. У двух углов общая вершина, каждый из этих углов равен 60⁰ (40⁰). 0бязательно ли эти углы вертикальные?

4. Может ли при пересечении двух прямых образоваться четыре тупых (острых) угла?

5. Сумма двух углов, образованных при пересечении двух прямых, равна 150⁰(170⁰ ). Могут эти углы быть вертикальными?

6. Один из углов, которые получаются при пересечении двух прямых, равен 40⁰ (120⁰ ). Найдите остальные углы.

7. Один из углов, которые получаются при пересечении двух прямых в 3 раза больше другого. Найдите эти углы.

8. Один из двух углов, который получается при пересечении двух прямых, в 8 раз меньше другого. Найти эти углы.

Диктант по теме: «Прямая и отрезок.»

Первый вариант.

1. Начертите прямую и обозначьте ее буквой а.

2. Отметьте точку D, не лежащую на прямой а.

3. Отметьте точку С, лежащую на прямой а.

4. Запишите символами предложение: «Точка С лежит на прямой b, а точка D не лежит на ней».

5. Даны две прямые а и b , пересекающиеся в точке С, и точка D,

отличная от точки С и лежащая на прямой а.

а) Выполните построение и запишите условие символами.

б) Может ли точка D лежать на прямой b?

6. На прямой b возьмите точки K, L, M. Запишите все образовавшиеся отрезки.

7. На плоскости даны три точки. Сколько прямых можно провести через эти точки так, чтобы на каждой прямой лежали хотя бы две из данных точек? Рассмотрите все возможные случаи и сделайте рисунки.

Второй вариант.

1. Начертите прямую и обозначьте её буквой b.

2. Отметьте точку М ,лежащую на прямой b.

3. Отметьте точку D, не лежащую на прямой b.

4. Используя математические символы запишите предложение : «Точка М лежит на прямой b ,а точка D не лежит на ней».

5. Начертите прямые а и b, пересекающиеся в точке К. На прямой а отметьте точку С , отличную от точки К.

а) Являются ли прямые КС и а различными прямыми ?

б) Может ли прямая b проходить через точку С?

1. На прямой а возьмите точки С, D ,Е. Запишите все образовавшиеся отрезки.

7. Сколько точек пересечения могут иметь три прямые? Рассмотрите все возможные случаи и сделайте соответствующие рисунки.

7 класс. Алгебра.

Диктант по теме: «Умножение многочленов.»

1. Ïðîäîëæèòå ïðåäëîæåíèå: «×òîáû óìíîæèòü ìíîãî÷ëåí íà ìíîãî÷ëåí, íóæíî …» («Â ðåçóëüòàòå óìíîæåíèÿ ìíîãî÷ëåíà íà ìíîãî÷ëåí …»).

2. Âûïîëíèòå äåéñòâèÿ: (3n ² – 2) (1 – 4 n) =; (a – 2) (3 + a) =; (3 – 4c)(2c ² – c – 1)=;(ñ + 5) (2c – 1) =.

3. Çàìåíèòå áóêâó «Ì» ìíîãî÷ëåíîì òàê, ÷òîáû ïîëó÷åííîå ðàâåíñòâî áûëî âåðíûì: 5à + Ì = 5à + 3b – 8; ( b² – bc —  Ì = b² – bc – 7b + 5;)        

4.  Óìíîæüòå ìíîãî÷ëåí õ – ó ( à + â ) íà ìíîãî÷ëåí õ +ó ( à – â ).

5. Óìíîæüòå ìíîãî÷ëåí õ + ó ( à — â ) íà ìíîãî÷ëåí x ² – õó + ó ²  (à²+ àâ + b²

6. Ïðåäñòàâüòå â âèäå ñòàíäàðòíîãî ìíîãî÷ëåíà êâàäðàò äâó÷ëåíà õ -2ó , ( à + 5â).

8класс. Алгебра.

Диктант по теме: «Функция у = х² , ее график.»

3. Функция задана формулой у = х² . Чему равно ее значение при х= -5 ( 6 ).

4. Принадлежит ли точка (-3, 9), [( — 4, 15)] графику функции у = х².

5. Значении функции у = х² при х = 12 ( -15 ) равно 144 ( 225 ), чему оно будет равно при х = -12 ( 15 ).

6. Аргумент равен -2. Найдите значение квадратичной функции у = х² + 3х – 5,

(у = 2х² – х + 4 ).

7. Найдите значение аргумента квадратичной функции у = х² – 9 (у = х² – х – 6),

если значение функции равно 0.

Автор: Гриднева Марина

учитель начальных классов.

Г. Санкт-Петербург ГБОУ школа №246

Математический диктант как форма контроля.

Одним из средств обратной связи между учителем и учеником служит математический диктант

Проведение математического диктанта на этапе устного счёта способствует не только развитию навыков вычисления ,но и повышению математической культуры. Польза устных вычислений огромна. Выполняя устно арифметические действия, дети не только повторяют правила арифметики, закрепляют их, но и, что самое главное, усваивают осмысленно. При устных вычислениях развиваются такие ценные качества, как внимание, сосредоточенность, выдержка, смекалка, самостоятельность. Математический диктант можно использовать как форму контроля уровня знаний учащихся , скорости вычислительных навыков.

Основное назначение математических диктантов – помочь учителю эффективно тренировать устойчивость внимания детей, память, умение сосредоточиваться, проверить вычислительные навыки, знание терминологии.

Проводить математические диктанты можно так:

1. Учитель читает вслух каждое задание диктанта два раза. Учащиеся на листочках или в тетрадях записывают ответы. При проверки следует показать верные ответы, обсудить решения отдельных заданий.

2. Полезно время от времени в классе давать всем ученикам тексты диктантов для самостоятельной работы с ними (записав текст диктанта и на доске). Это важно для запоминания правописания математических терминов.

3. Математические диктанты можно давать и для домашней работы под руководством родителей. Это позволит каждому ученику дополнительно спокойно потренироваться в чтении математических текстов, не спеша разобраться в отдельных задачах, проверить свои знания.

Учителю читать диктант детям можно и один раз. Это заставляет учеников быть предельно внимательными и собранными. Все вычисления и преобразования ученики выполняют только устно.

Обязательное требование проводить математические диктанты систематически, а не от случая к случаю, в этом и состоит результативность.. Задания учатся писать на слух. Ценность такого навыка неоспорима- она приводит к умению слушать. В своё время критик Писарев применительно к значению математических диктантов писал:

« Смышлёность учеников растёт постоянно во время математических занятий, что так же верно и неизбежно, как то, что мускулы человека и ловкость его увеличиваются, когда он занимается гимнастическими упражнениями.»

Математический диктант (1 класс)

1. Запишите число, которое предшествует числу 11…

2. Увеличьте 10 на 3.

3. Уменьшите 18 на 1.

4. Какое число меньше 14 на 1?

5. На сколько 15 больше 7?

6. Первое слагаемое 8, второе 3. Найдите сумму.

7. Сколько надо прибавить к 5, чтобы получить 14?

8. Чему равна сумма, если первое слагаемое 6, а второе 9?

9. В гараже было 5 машин, приехало еще 3 машины. Сколько машин стало в гараже?

10.Запиши число которое следует за числом 17

Математический диктант. (2 класс)

1. У бабушки в хозяйстве 5 кур и 7 гусей. Сколько всего птиц у Бабушки?

2. У ПЕСТРОЙ КУРОЧКИ 3 ЦЫПЛЕНКА, А У БЕЛОЙ 9. Во сколько раз У пестрой курочки цыплят меньше ?

3. Бабушка принесла 9 яиц , 3 яйца она вбила в тесто, а остальные сварила. Сколько яиц сварила бабушка ?

4. В сарае 4 гнезда , в каждом по 3 яйца. Сколько всего яиц в гнездах ?

5. Бабушка купила 5 уточек и у нее стало 8 уточек . Сколько было у бабушки уточек?

6. Бабушка испекла 12 пирожков каждому из внучат по 3. Сколько внучат у бабушки?

7. Бабушка испекла 6 пирожков с капустой , что на 2 пирожка меньше чем с картошкой. Сколько с картошкой пирожков?

8. Бабушка разложила по 4 яблока на 2 тарелки и у нее осталось еще 2 яблока . Сколько всего было яблок у бабушки ?

9. В хозяйстве 7 гусей и 9 уток . На сколько больше уток чем гусей ?

10. Сколько всего гусей и уток , если гусей 8 и уток столько же ?

Математический диктант. (2 класс — табличное умножение)

Увеличить число 8 в 6 раз

Уменьшить число 28 в 4 раза

Делимое 81, делитель 9. Чему равно частное?

Первый множитель 8, второй множитель 3. Чему равно произведение

Сколько ушей у 9 ежей?

Сколько лап у 7 тигрят?

Сколько хвостов у 10 ослов?

Я задумала число, умножила его на 8 и получила 64. Какое число я задумала?

На сколько 48 больше чем 8?

Во сколько раз 48 больше чем 8?

Математический диктант. (3 класс)

Какое число предшествует числу 307

Какое число является последующим для числа 419

Чему равна сумма чисел320 и 30?

У Веры 90 открыток , это в 3 раза больше чем у Севы. Сколько открыток у Севы?

Когда папа дал Васе 50 рублей, то у Васи стало 90. Сколько рублей было у Васи?

Гена нашел 30 грибов и Сева столько же. Сколько грибов собрали мальчики?

Назовите соседей числа 283

У Саши 80 марок, а у Севы 20. Во сколько раз у Саши марок больше чем у Севы?

Чему равно произведение чисел 25 и 0 ?

Чему равно частное чисел 60 и 1 ?

Математический диктант. (4 класс)

На сколько число 5300 больше чем 100?

Чему равно делимое, если делитель равен 100, а частное 900

Увеличьте число 3200 в 2 раза.

Во сколько раз число10 меньше 800?

Чему равно вычитаемое, если уменьшаемое равно 4200, а разность 2000?

Запиши число в котором 6 единиц первого класса и столько же второго.

Уменьшить число 3800 на 900

Чему равна разность чисел 6500 и 300?

Найдите сумму чисел 7300 и300

Произведение чисел 400 и20 разделить на 8

Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/431294-matematicheskij-diktant-kak-forma-kontrolja