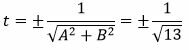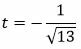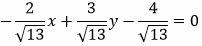В данной статье рассмотрим нормальное уравнение прямой на заданной плоскости. Получим нормальное уравнение, покажем не примере, дадим определение нормирующего множителя и разберем приведение общего уравнения к нормальному виду. Заключительной части посвятим основному приложению нормального уравнения прямой, то есть нахождение расстояние от точки до прямой на плоскости.
Нормальное уравнение прямой – описание и пример
Рассмотрим выведение нормального уравнения.
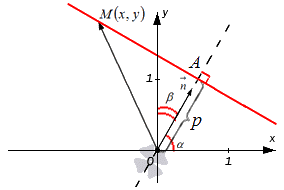
Фиксируем на плоскости систему координат Оху, где задаем прямую с точкой, через которую она проходит с нормальным вектором прямой. Нормальному вектору прямой дадим обозначение n→. Его начало обозначено точкой O. координатами являются cos α и cos β, углы которых расположены между вектором n→ и положительными осями Оx и Oy. Это запишется так: n→=(cos α, cos β). Прямая проходит через точку A с расстоянием равным p, где p≥0 от начальной точки O при положительном направлении вектора n→. Если р=0, тогда A считается совпадающей с точкой координат. Отсюда имеем, что OA=p. Получаем уравнение, при помощи которого задается прямая.
Имеем, что точка с координатами M (x, y) расположена на прямой тогда и только тогда, когда числовая проекция вектора OM→ по направлению вектора n→ равняется p, значит при выполнении условия npn→OM→=p.
OM→ является радиус-вектором точки с координатами M (x, y), значит OM→=(x, y).
Применив определение скалярного произведения векторов, получим равенство вида: n→, OM→=n→·npn→OM→=1·npn→OM→=npn→OM→=p
Тогда это же произведение будет иметь вид в координатной форме: n→, OM→=cos α·x+cos β·y
Отсюда cos α·x+cos β·y=p или cos α·x+cos β·y-p=0. Было выведено нормальное уравнение прямой.
Уравнение вида cos α·x+cos β·y-p=0 называется нормальным уравнением прямой или нормированным уравнением прямой. Иначе говоря, уравнение прямой в нормальном виде.
Понятно, что такое уравнение представляет собой общее уравнение прямой Ax+By+C=0, где A и B имеют значения, при которых длина вектора n→=(A, B) равна 1, а C является неотрицательным числом.
Теперь рассмотрим его геометрический смысл. Нормальное уравнение прямой вида cos α·x+cos β·y-p=0 задает в системе координат Оху на плоскости прямую с наличием нормального вектора единичной длины n→=(cos α, cos β), которая располагается на расстоянии равном p от начала координат по положительному направлению вектора n→.
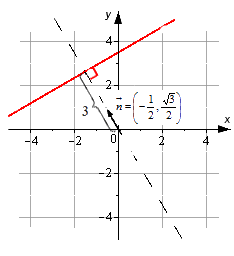
Если дано уравнение прямой вида -12·x+32·y-3=0, то на плоскости задается прямая, у которой нормальный вектор с координатами -12, 32. Удаление прямой от начала координат идет по направлению, совпадающему с направлением нормального вектора n→=-12, 32.
Приведение общего уравнения прямой к нормальному виду
Часто решение задач подразумевает использование нормального уравнения прямой, но само оно не дается в нормальном виде, поэтому необходимо для начала приводить к нормальному виду, после чего выполнять необходимые вычисления.
Нормальное уравнение получают из общего уравнения прямой. Когда на плоскости задается другим уравнением, то необходимо привести его к общему виду, после чего возможно приведение к нормальному. Если рассмотреть на примере, то это будет выглядеть так.
Для приведения общего уравнения прямой Ax+Bx+C=0 к нормальному необходимо обе части умножить на нормирующий множитель, который имеет значение ±1A2+B2. Его знак определяется при помощи противоположности знака слагаемого C. При С=0 знак выбирается произвольно.
Привести уравнение прямой 3x-4y-16=0 к нормальному виду.
Решение
Из общего уравнения видно, что А=3, В=-4, С=-16. Так как значение C отрицательное, необходимо брать положительный знак для формулы. Перейдем к вычислению нормирующего множителя:
1A2+B2=132+(-4)2=15
Теперь необходимо умножить обе части уравнения на одну пятую. Получим, что 15·(3x-4y-16)=0⇔35·x-45·y-165=0.
Нормальное уравнение по заданной прямой найдено.
Ответ: 35·x-45·y-165=0.
Получить нормальное уравнение прямой y=13x.
Решение
По условию имеем, что общее уравнение прямой 13x-y=0. Очевидно, что С=0, значит знак нормирующего множителя не имеет значения. Выбираем со знаком «+». Тогда выражение примет вид:
1A2+B2=1132+(-1)2=310
Обе части умножаем на нормированный множитель, получаем, что нормальное уравнение прямой имеет вид 110x-310y=0.
Ответ: 110x-310y=0.
Нахождение расстояния от точки до прямой на плоскости
В данном пункте рассмотрим важное приложение нормального уравнения прямой – нахождение расстояния от заданной точки до заданной прямой на плоскости.
Расстояние от точки M0(x0, y0) до прямой с нормальным уравнением cos α·x+cos β·y-p=0 задается буквой p. Вычисление расстояния р производится по формуле p=cos α·x0+cos β·y0-p. Для того, чтобы найти расстояние от точки до прямой, нужно сделать подстановку координат этой точки в левую часть уравнения и работать с абсолютной величиной полученного значения. С подробным выводом формулы можно ознакомиться в статье нахождения расстояния от точки до прямой. Имеется альтернативный способ его вычисления.
Найти расстояния от точки с координатами M0(-2, 1) к прямой с нормальным уравнением 23x-52y-1=0.
Решение
По условию имеем, что x0=-2, y0=1, cos α=23, cos β=-53, p=1.
Применим формулу для вычисления расстояния от точки до прямой. Получим, что:
p=cos α·x0+cos β·y0-p=23·-2-53·1-1=-7+53=7+53
Ответ: 7+53.
Вычислить расстояние от точки с координатами M0(-2, -3) до прямой x-1-2=y+33.
Решение
Начнем решение с приведения уравнения заданной прямой к нормальному виду. Для начала необходимо привести к общему виду. Получим:
x-1-2=y+33⇔3·(x-1)=-2·(y+3)⇔3x+2y+3=0
Проведем вычисление нормирующего множителя по формуле: -1A2+B2=-132+22=-113.
Следующим действием будет умножение обоих частей уравнения 3x+2y+3=0 на нормирующий множитель.
Получаем: -313·x-213·y-313=0
Было произведено получение нормального уравнения прямой. Чтобы найти расстояние, необходимо использовать абсолютную величину и подставить в формулу для нахождения искомого значения.
Тогда p=-313·(-2)-213·(-3)-313=913=913.
Ответ: 913.
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Нормальное уравнение прямой
В данной статье мы рассмотрим нормальное уравнение прямой на плоскости. Приведем примеры построения нормального уравнения прямой по углу наклона нормального вектора прямой от оси Ox и по расстоянию от начала координат до прямой. Представим метод приведения общего уравнения прямой к нормальному виду. Рассмотрим численные примеры.
Пусть на плоскости задана декартова прямоугольная система координат. Тогда нормальное уравнение прямой L на плоскости представляется следующей формулой:
где r− расстояние от начала координат до прямой L, а φ− это угол между нормальным вектором n прямой L и осью Ox. (Если r>0, то нормальный вектор n направлен в сторону прямой L).
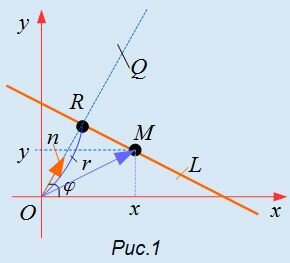
Выведем формулу (1). Пусть на плоскости задана декартова прямоугольная система координат и прямая L (Рис.1). Проведем через начало координат прямую Q, перпендикулярную прямой L, и точку пересечения обозначим через R. На этой прямой выделим единичный вектор n, с направлением, совпадающим с вектором 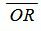
Выразим уравнение прямой L через два параметра: длину отрезка 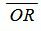
Так как вектор n является единичным вектором, то его проекции на Ox и Oy будут иметь следующие координаты:
Обозначим через r расстояние от начала координат до точки R. Рассмотрим, теперь, точку M(x,y). Точка M лежит на прямой L тогда и только тогда, когда проекция вектора 
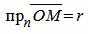 |
(3) |
Скалярное произведение векторов n и 
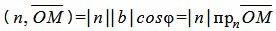 , , |
(4) |
где 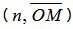


Поскольку n единичный вектор, то (4) можно записать так:
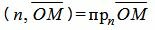 . . |
(5) |
Учитывая, что n=<cosφ, sinφ>, 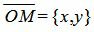
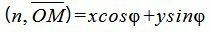 . . |
(6) |
Тогда из уравнений (3), (5), (6) следует:
Мы получили нормальное уравнение прямой L. Уравнение (7) (или (1)) называется также нормированным уравнением прямой .
Пример 1. Построить нормальное уравнение прямой, нормальный вектор которого с осью Ox имеет угол φ=60°, а расстояние от начала координат до прямой составляет 4.
Решение. Имеем: φ=60°, r=4. Вычисляем:
Подставляя вычисленные значения в (7) получим:
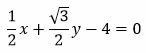
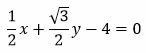
Приведение общего уравнения прямой на плоскости к нормальному виду
Так как уравнения (1) и (8) должны определять одну и ту же прямую (Замечание 1 статьи «Общее уравнение прямой на плоскости»), то существует такое число t, что
| tAx=cosφ, tB=sinφ, tC=−r. | (9) |
Возвышая в квадрат первые два равенства в (9) и складывая их, получим:
| (tA) 2 +(tB) 2 =cos 2 φ+sin 2 φ=1. | (10) |
Упростим выражение и найдем t:
t 2 A 2 +t 2 B 2 =t 2 (A 2 +B 2 )=1,
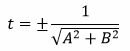 . . |
(11) |
Знаменатель в (11) отличен от нуля, т.к. хотя бы один из коэффициентов A, B не равен нулю (в противном случае (8) не представлял бы уравнение прямой).
Выясним, какой знак имеет t. Обратим внимание на третье равенство в (9). Так как r−это расстояние от начала координат до прямой, то r≥0. Тогда произведение tC должна иметь отрицательный знак. Т.е. знак t в (11) должен быть противоположным знаку C.
Подставляя в (1) вместо cosφ, sinφ, и −r значения из (9), получим tAx+tBy+tC=0. Т.е. для приведения общего уравенения прямой к нормальному виду, нужно заданное уравнение умножить на множитель (11). Множитель (11) называется нормирующим множителем .
Пример 2. Задано общее уравнение прямой
Построить нормальное уравнение прямой.
Решение. Из уравнения (12) можно записать: A=2, B=−3, C=4. Вычислим t из равенства (11):
Так как C>0, то знак t отрицательный:
Умножим уравнение (12) на t:
Ответ. Нормальное уравнение прямой (12) имеет следующий вид:
Отметим, что число 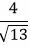
Нормальное уравнение прямой на плоскости, расстояние от точки до прямой
Пусть дана некоторая прямая L. Проведём через начало координат прямую n, перпендикулярно данной и назовём её нормалью к прямой L. Буквой N отметим точку, в которой нормаль пересекает прямую L. На нормали введём направление от точки O к точке N.
Обозначим через 

будет нормальным уравнением прямой.
С помощью нормального уравнения прямой можно определить расстояние от данной точки плоскости до прямой. Пусть 

Общее уравнение прямой можно привести к нормальному виду. Пусть
— общее уравнение прямой, а
— её нормальное уравнение.
Так как оба уравнения определяют одну и ту же прямую, их коэффициенты пропорциональны.
Очевидно, для получения нормального уравнения следует все члены общего уравнения умножить на постоянный множитель 

В этой формуле берётся знак, противоположный знаку C в общем уравнении прямой.
Таким образом, получаем уравнение

которое и будет нормальным уравнением прямой на плоскости.
Пример 1. Привести общее уравнение прямой 
Решение. Вычисляем нормирующий множитель:

Умножаем все члены общего уравнения на нормирующий множитель и получаем:

Пример 2. Привести общее уравнение прямой 
Решение. Вычисляем нормирующий множитель:

Умножаем все члены общего уравнения на нормирующий множитель и получаем:

Пример 3. Найти расстояние от точки 

Решение. Приведём данное уравнение к нормальному виду. Вычисляем нормирующий множитель:

Умножаем все члены общего уравнения на нормирующий множитель и получаем нормальное уравнение:

По формуле (2) находим искомое расстояние:

Нормальное (нормированное) уравнение прямой: описание, примеры, решение задач
В данной статье рассмотрим нормальное уравнение прямой на заданной плоскости. Получим нормальное уравнение, покажем не примере, дадим определение нормирующего множителя и разберем приведение общего уравнения к нормальному виду. Заключительной части посвятим основному приложению нормального уравнения прямой, то есть нахождение расстояние от точки до прямой на плоскости.
Нормальное уравнение прямой – описание и пример
Рассмотрим выведение нормального уравнения.
Фиксируем на плоскости систему координат О х у , где задаем прямую с точкой, через которую она проходит с нормальным вектором прямой. Нормальному вектору прямой дадим обозначение n → . Его начало обозначено точкой O . координатами являются cos α и cos β , углы которых расположены между вектором n → и положительными осями О x и O y . Это запишется так: n → = ( cos α , cos β ) . Прямая проходит через точку A с расстоянием равным p , где p ≥ 0 от начальной точки O при положительном направлении вектора n → . Если р = 0 , тогда A считается совпадающей с точкой координат. Отсюда имеем, что O A = p . Получаем уравнение, при помощи которого задается прямая.
Имеем, что точка с координатами M ( x , y ) расположена на прямой тогда и только тогда, когда числовая проекция вектора O M → по направлению вектора n → равняется p , значит при выполнении условия n p n → O M → = p .
O M → является радиус-вектором точки с координатами M ( x , y ) , значит O M → = ( x , y ) .
Применив определение скалярного произведения векторов, получим равенство вида: n → , O M → = n → · n p n → O M → = 1 · n p n → O M → = n p n → O M → = p
Тогда это же произведение будет иметь вид в координатной форме: n → , O M → = cos α · x + cos β · y
Отсюда cos α · x + cos β · y = p или cos α · x + cos β · y — p = 0 . Было выведено нормальное уравнение прямой.
Уравнение вида cos α · x + cos β · y — p = 0 называется нормальным уравнением прямой или нормированным уравнением прямой. Иначе говоря, уравнение прямой в нормальном виде.
Понятно, что такое уравнение представляет собой общее уравнение прямой A x + B y + C = 0 , где A и B имеют значения, при которых длина вектора n → = ( A , B ) равна 1 , а C является неотрицательным числом.
Теперь рассмотрим его геометрический смысл. Нормальное уравнение прямой вида cos α · x + cos β · y — p = 0 задает в системе координат О х у на плоскости прямую с наличием нормального вектора единичной длины n → = ( cos α , cos β ) , которая располагается на расстоянии равном p от начала координат по положительному направлению вектора n → .
Если дано уравнение прямой вида — 1 2 · x + 3 2 · y — 3 = 0 , то на плоскости задается прямая, у которой нормальный вектор с координатами — 1 2 , 3 2 . Удаление прямой от начала координат идет по направлению, совпадающему с направлением нормального вектора n → = — 1 2 , 3 2 .
Приведение общего уравнения прямой к нормальному виду
Часто решение задач подразумевает использование нормального уравнения прямой, но само оно не дается в нормальном виде, поэтому необходимо для начала приводить к нормальному виду, после чего выполнять необходимые вычисления.
Нормальное уравнение получают из общего уравнения прямой. Когда на плоскости задается другим уравнением, то необходимо привести его к общему виду, после чего возможно приведение к нормальному. Если рассмотреть на примере, то это будет выглядеть так.
Для приведения общего уравнения прямой A x + B x + C = 0 к нормальному необходимо обе части умножить на нормирующий множитель, который имеет значение ± 1 A 2 + B 2 . Его знак определяется при помощи противоположности знака слагаемого C . При С = 0 знак выбирается произвольно.
Привести уравнение прямой 3 x — 4 y — 16 = 0 к нормальному виду.
Из общего уравнения видно, что А = 3 , В = — 4 , С = — 16 . Так как значение C отрицательное, необходимо брать положительный знак для формулы. Перейдем к вычислению нормирующего множителя:
1 A 2 + B 2 = 1 3 2 + ( — 4 ) 2 = 1 5
Теперь необходимо умножить обе части уравнения на одну пятую. Получим, что 1 5 · ( 3 x — 4 y — 16 ) = 0 ⇔ 3 5 · x — 4 5 · y — 16 5 = 0 .
Нормальное уравнение по заданной прямой найдено.
Ответ: 3 5 · x — 4 5 · y — 16 5 = 0 .
источники:
http://function-x.ru/line6.html
http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/normalnoe-normirovannoe-uravnenie-prjamoj/
Нормальное уравнение прямой
В данной статье мы рассмотрим нормальное уравнение прямой на плоскости. Приведем примеры построения нормального уравнения прямой по углу наклона нормального вектора прямой от оси Ox и по расстоянию от начала координат до прямой. Представим метод приведения общего уравнения прямой к нормальному виду. Рассмотрим численные примеры.
Пусть на плоскости задана декартова прямоугольная система координат. Тогда нормальное уравнение прямой L на плоскости представляется следующей формулой:
где r− расстояние от начала координат до прямой L, а φ− это угол между нормальным вектором n прямой L и осью Ox. (Если r>0, то нормальный вектор n направлен в сторону прямой L).
Выведем формулу (1). Пусть на плоскости задана декартова прямоугольная система координат и прямая L (Рис.1). Проведем через начало координат прямую Q, перпендикулярную прямой L, и точку пересечения обозначим через R. На этой прямой выделим единичный вектор n, с направлением, совпадающим с вектором 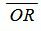
Выразим уравнение прямой L через два параметра: длину отрезка 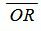
Так как вектор n является единичным вектором, то его проекции на Ox и Oy будут иметь следующие координаты:
Обозначим через r расстояние от начала координат до точки R. Рассмотрим, теперь, точку M(x,y). Точка M лежит на прямой L тогда и только тогда, когда проекция вектора 
Скалярное произведение векторов n и 
где 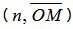


Поскольку n единичный вектор, то (4) можно записать так:
Учитывая, что n={cosφ, sinφ}, 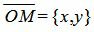
Тогда из уравнений (3), (5), (6) следует:
или
Мы получили нормальное уравнение прямой L. Уравнение (7) (или (1)) называется также нормированным уравнением прямой.
Пример 1. Построить нормальное уравнение прямой, нормальный вектор которого с осью Ox имеет угол φ=60°, а расстояние от начала координат до прямой составляет 4.
Решение. Имеем: φ=60°, r=4. Вычисляем:
Подставляя вычисленные значения в (7) получим:
Ответ:
Приведение общего уравнения прямой на плоскости к нормальному виду
Пусть на плоскости задано уравнение прямой в общем виде:
Так как уравнения (1) и (8) должны определять одну и ту же прямую (Замечание 1 статьи «Общее уравнение прямой на плоскости»), то существует такое число t, что
Возвышая в квадрат первые два равенства в (9) и складывая их, получим:
Упростим выражение и найдем t:
Знаменатель в (11) отличен от нуля, т.к. хотя бы один из коэффициентов A, B не равен нулю (в противном случае (8) не представлял бы уравнение прямой).
Выясним, какой знак имеет t. Обратим внимание на третье равенство в (9). Так как r−это расстояние от начала координат до прямой, то r≥0. Тогда произведение tC должна иметь отрицательный знак. Т.е. знак t в (11) должен быть противоположным знаку C.
Подставляя в (1) вместо cosφ, sinφ, и −r значения из (9), получим tAx+tBy+tC=0. Т.е. для приведения общего уравенения прямой к нормальному виду, нужно заданное уравнение умножить на множитель (11). Множитель (11) называется нормирующим множителем.
Пример 2. Задано общее уравнение прямой
Построить нормальное уравнение прямой.
Решение. Из уравнения (12) можно записать: A=2, B=−3, C=4. Вычислим t из равенства (11):
Так как C>0, то знак t отрицательный:
Умножим уравнение (12) на t:
Ответ. Нормальное уравнение прямой (12) имеет следующий вид:
Отметим, что число 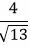
Пусть
– фиксированная точка плоскости,
– вектор, заданный своими направляющими
косинусами, тогда уравнение вида
задает прямую на плоскости, проходящую
через точку
перпендикулярно вектору
,
который называется нормальным
вектором этой прямой. Запишем скалярное
произведение вектора
и вектора
в координатной форме:
|
|
(8) |
Теперь, введя
обозначение
получим нормальное уравнение прямой:
|
|
(9) |
|
Рис. 3 |
где – угол наклона перпендикуляра, – угол наклона этого перпендикуляра
Общее уравнение |
взятый со знаком,
противоположным знаку свободного члена.
1.10. Полярные параметры прямой
Полярными
параметрами можно задать положение
всякой прямой на плоскости.
|
Рис. |
Полярным между положительным направлением |
оси Ох и
перпендикуляром, опущенным на прямую
из начала координат. Полярное расстояние
и полярный угол называются полярными
параметрами прямой. При этом нормальное
уравнение прямой можно записать в виде:
|
|
(10) |
2. Прямые на плоскости: взаимное расположение
Утверждение 2.
Пусть на
плоскости заданы две прямые:
и
В этом случае выполняется одно и только
одно из трех условий:
1) прямые не имеют
общих точек
при этом система линейных алгебраических
уравнений
несовместна (имеет пустое множество
решений);
2) прямые имеют
единственную общую точку
при этом система линейных алгебраических
уравнений
имеет единственное решение
которое может быть найдено, например,
по формулам Крамера:
|
|
(11) |
|
(12) |
3) прямые совпадают
при этом система линейных алгебраических
уравнений
не определена (имеет бесконечно много
решений).
2.1. Условие, при котором три точки лежат на одной прямой
Три точки
,
,
лежат на одной прямой тогда и только
тогда, когда определитель
|
|
(13) |
Равенство нулю
определителя (13) означает, что площадь
«треугольника»
равна нулю.
2.2. Взаимное расположение прямой и пары точек
Пусть заданы точки
и общее уравнение некоторой прямой: Ax
+ By + C
= 0. Вычислим значения величин
и
по формулам:
|
|
(14) |
|
(15) |
Взаимное расположение
точек
и
относительно заданной прямой можно
определить по следующим признакам:
1) числа
и
имеют одинаковые знаки, в этом случае
точки
и
лежат по одну сторону от прямой;
2) числа
и
имеют противоположные знаки, в этом
случае точки
и
лежат по разные стороны от прямой;
3) одно из чисел
,
равно нулю (или оба равны нулю), в этом
случае точка
или
соответственно (или обе) принадлежит
прямой.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Прямая имеет несколько видов задающих ее уравнений. Рассмотрим некоторые из них и разберем примеры.
Здесь будет калькулятор
Уравнение прямой с угловым коэффициентом
y=kx+by=kx+b,
где kk — угловой коэффициент, а bb — свободный коэффициент.
Уравнения данного вида составляются следующим образом по формуле:
y−y0=k(x−x0)y-y_0=k(x-x_0),
где (x0;y0)(x_0; y_0) — координаты любой точки, лежащей на данной прямой.
Составить уравнение прямой, если координаты точки, принадлежащей данной прямой, таковы: x0=1,y0=2x_0=1, y_0=2. Угловой коэффициент принять равным 11.
Решение
Подставляем значения в формулу:
y−y0=k(x−x0)y-y_0=k(x-x_0)
y−2=1⋅(x−1)y-2=1cdot(x-1)
Приводим подобные слагаемые:
y=x+1y=x+1
Ответ
y=x+1y=x+1
Общее уравнение прямой
Для приведения прямой к такому виду из предыдущего вида достаточно просто перенести все слагаемые в одну часть. Возьмем уравнение прямой из предыдущей задачи y=x+1y=x+1. Тогда общее уравнение этой прямой запишется в виде:
y−x−1=0y-x-1=0
Уравнение прямой по двум точкам
Если в задаче даны координаты двух точек и необходимо составить уравнение прямой, то это делается при помощи такой формулы:
x−x2x1−x2=y−y2y1−y2frac{x-x_2}{x_1-x_2}=frac{y-y_2}{y_1-y_2},
где (x1;y1),(x2;y2)(x_1; y_1), (x_2; y_2) — координаты двух точек, через которые проходит данная прямая.
Найти уравнение прямой, если координаты точек имеют значения: (2;3)(2;3) и (4;−1)(4;-1).
Решение
x1=2x_1=2
y1=3y_1=3
x2=4x_2=4
y2=−1y_2=-1
x−x2x1−x2=y−y2y1−y2frac{x-x_2}{x_1-x_2}=frac{y-y_2}{y_1-y_2}
x−42−4=y−(−1)3−(−1)frac{x-4}{2-4}=frac{y-(-1)}{3-(-1)}
x−4−2=y+14frac{x-4}{-2}=frac{y+1}{4}
x−4=−y−12x-4=frac{-y-1}{2}
y+1=2⋅(4−x)y+1=2cdot(4-x)
y=8−2x−1y=8-2x-1
y=−2x+7y=-2x+7
Ответ
y=−2x+7y=-2x+7
Уравнение прямой при помощи точки и вектора нормали
(x−x0)⋅n1+(y−y0)⋅n2=0(x-x_0)cdot n_1+(y-y_0)cdot n_2=0,
где (x0;y0)(x_0; y_0) — координаты точки, лежащей на данной прямой, а (n1;n2)(n_1; n_2) — координаты вектора нормали к этой прямой.
Составить уравнение прямой, если координаты нормального вектора — (1;−5)(1;-5), а точка, через которую проходит данная прямая имеет координаты (7;8)(7;8).
Решение
x0=7x_0=7
y0=8y_0=8
n1=1n_1=1
n2=−5n_2=-5
(x−x0)⋅n1+(y−y0)⋅n2=0(x-x_0)cdot n_1+(y-y_0)cdot n_2=0,
(x−7)⋅1+(y−8)⋅(−5)=0(x-7)cdot 1+(y-8)cdot (-5)=0,
x−7+40−5y=0x-7+40-5y=0
x−5y=−40+7x-5y=-40+7
x−5y=−33x-5y=-33
5y=x+335y=x+33
y=x5+335y=frac{x}{5}+frac{33}{5}
Проверка
Чтобы проверить правильность решения, достаточно подставить координаты точки в данное уравнение и, если оно будет верным, то задача решена верно.
8=75+3358=frac{7}{5}+frac{33}{5}
8=88=8 — верно, ответ правильный.
Ответ
y=x5+335y=frac{x}{5}+frac{33}{5}
Прямая в пространстве
Уравнение прямой, заданной в пространстве имеет такой вид:
x−x0ν1=y−y0ν2=z−z0ν3frac{x-x_0}{nu_1}=frac{y-y_0}{nu_2}=frac{z-z_0}{nu_3},
где (x0;y0;z0)(x_0;y_0;z_0) — координаты точки, через которую проходит прямая, а (ν1,ν2,ν3)(nu_1,nu_2,nu_3) — координаты напрявляющего вектора данной прямой.
Написать уравнение прямой по заданной точке (1;5;−23)(1;5;-23) и вектору направления (3;11;7)(3;11;7).
Решение
x0=1x_0=1
y0=5y_0=5
z0=−23z_0=-23
ν1=3nu_1=3
ν2=11nu_2=11
ν3=7nu_3=7
x−x0ν1=y−y0ν2=z−z0ν3frac{x-x_0}{nu_1}=frac{y-y_0}{nu_2}=frac{z-z_0}{nu_3}
x−13=y−511=z−(−23)7frac{x-1}{3}=frac{y-5}{11}=frac{z-(-23)}{7}
Проверка
Проверим, удовлетворяет ли это уравнение прямой точке (x0;y0;z0)(x_0;y_0;z_0). Для этого подставим в него координаты этой точки:
1−13=5−511=−23−(−23)7frac{1-1}{3}=frac{5-5}{11}=frac{-23-(-23)}{7} — верно, значит ответ правильный.
Такой вид уравнения прямой называется каноническим.
Ответ
x−13=y−511=z−(−23)7frac{x-1}{3}=frac{y-5}{11}=frac{z-(-23)}{7}