Квадратурный демодулятор, или I/Q demodulator, находит применение в SDR приемниках и трансиверах, а также в приемниках прямого преобразования с аналоговым подавлением зеркального канала, как сделано в QCX. Давайте же разберемся, что это за демодулятор такой, и рассмотрим одну из возможных его реализаций.
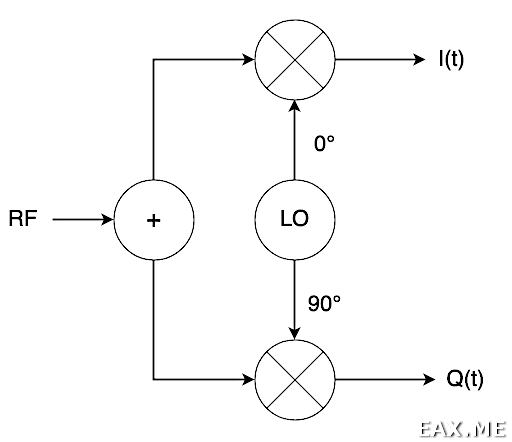
Вот структурная схема квадратурного демодулятора:
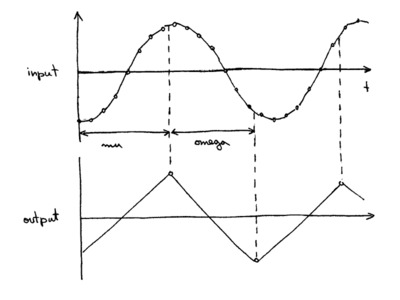
ВЧ сигнал попадает на делитель, после чего идет на пару смесителей. Сигнал гетеродина (LO), поступающий на смесители, имеет одинаковую частоту и отличается только фазовым сдвигом. Выход I(t) называют синфазным сигналом, или in-phase, а Q(t) — квадратурным сигналом, или quadrature. В чем состоит практическая польза такой схемы, будет показано далее.
Если изменить направление сигналов (вход справа, выход слева), получим квадратурный модулятор, или I/Q modulator. Иногда встречается термин квадратурный смеситель, или I/Q mixer, когда не уточняется, используется ли схема в роли модулятора или демодулятора. Модуляцию в рамках этой статьи мы рассматривать не будем. По этой теме могу порекомендовать видео IQ Modulator Basics: Operation, Measurements, Impairments, снятое Alan Wolke, W2AEW. Помимо прочего, из видео вы узнаете, как получить BPSK и QPSK сигналы.
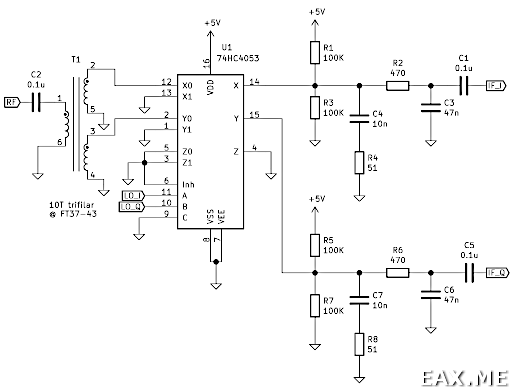
На практике квадратурный демодулятор часто реализуют на основе шинных переключателей 74HC4053, FST3253 и подобных. Одна из возможных схем выглядит так (файл PDF):
Трансформатор T1 здесь выступает в роли простого делителя. Выходы X и Y переключаются между землей и сигналом ВЧ (RF). Это эквивалентно умножению на 0 и 1, или меандр, частота которого задается гетеродином (LO). Дальше сигнал проходит через диплексеры и RC-фильтры.
Как результат, на выходах IF_I и IF_Q остается только НЧ сигнал:
В роли гетеродина был использован самодельный генератор сигналов на Si5351. Он позволяет генерировать сигналы с фазовым сдвигом 90°. Частота гетеродина фиксированная — 7.100 МГц.
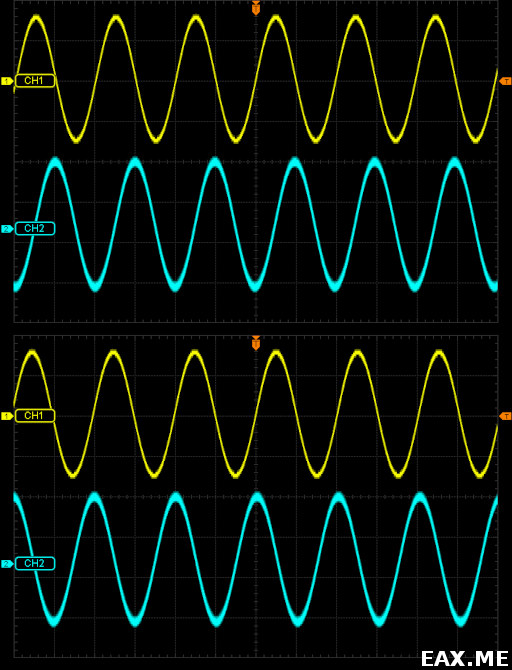
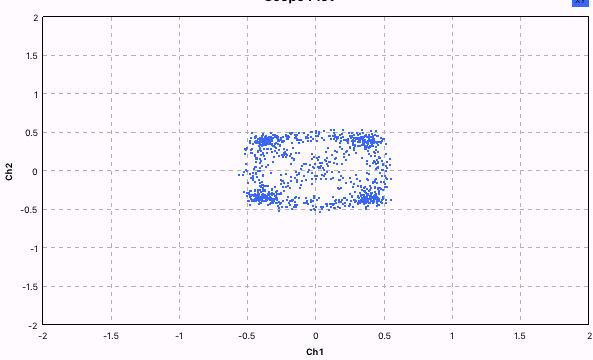
На первой осциллограмме принимается сигнал с частотой 7.101 МГц, а на второй осциллограмме — 7.099 МГц. Обратите внимание на фазы синфазного (желтый) и квадратурного (синий) сигналов. В первом случае синфазный сигнал опережает квадратурный на 90°, а во втором — отстает на 90°. Другими словами, по паре сигналов I и Q мы можем определить, находится ли принимаемый сигнал выше частоты гетеродина или ниже.
Важно! В этом заключается принципиальное отличие от приемника прямого преобразования. Обычный ППП не может определить, принимает ли он сигнал выше или ниже частоты гетеродина. Поэтому устранить прием зеркального канала не представляется возможным.
Оказывается, что этой информации достаточно, например, чтобы подавить верхнюю боковую полосу и принять только нижнюю. В SDR-приемниках это осуществляется при помощи цифровой обработки сигналов (DSP). В трансивере QCX качественно та же математика реализована «в железе» на операционных усилителях. Помимо CW и SSB могут быть приняты и более сложные сигналы, например, ЧМ или QAM. Конкретные схемы и алгоритмы заслуживают отдельных постов.
Приведенный демодулятор имеет некоторые недостатки, ну или особенности, это уже как посмотреть. Во-первых, входной импеданс на порту RF составляет 125-150 Ом на КВ, в зависимости от частоты. Если стоит задача получить ~50 Ом, придется подобрать другое число витков на первичной обмотке T1. Во-вторых, выходы IF_I и IF_Q не тянут низкоомную нагрузку. В-третьих, имеются вносимые потери. При подаче 1 Vpp (High-Z) на порт RF на портах IF_I и IF_Q получаем по 0.25 Vpp.
Из хорошего — схема демонстрирует стабильную работу на частотах до 100 МГц. Это максимальная частота, которую мой драйвер Si5351 может генерировать с фазовым сдвигом 90°. Судя по даташиту [PDF] на 74HC4053, в пределе демодулятор должен работать на частотах где-то до 200 МГц. Ищите параметр Fmax, «Minimum Switch Frequency Response at -3dB».
Рассмотренный материал важен для понимания теории. Но в современных устройствах часто применяется другая схема — детектор Тейло. С ним мы познакомимся в другой раз.
Дополнение: В продолжение темы см также пост Сдвиг фазы аудио-сигнала на 90° при помощи ОУ.
Метки: SDR, Беспроводная связь, Любительское радио, Электроника.
При создании радиолюбительских приёмников или трансиверов часто возникает задача разработки АМ/ЧМ демодулятора как для узкополосных сигналов, так и для широкополосного ЧМ-радиовещания. Принцип работы большинства таких демодуляторов основан на аналоговой обработке сигнала с помощью частотных или амплитудных детекторов. Концепция развития современных SDR-приёмников (Software Defined Radio) подразумевает программное управление синтезаторами частоты и другими узлами с помощью микроконтроллера. В связи с этим становится заманчивым использование управляющего микроконтроллера и для задач цифровой обработки сигналов.
В этой статье представлены результаты исследования по применению микроконтроллеров STM32F405/407 фирмы STMic-roelectronics. В большинстве случаев такая задача решается с помощью применения цифровых сигнальных процессоров (DSP) или ПЛИС (FPGA), однако в радиолюбительских целях применение подобных устройств зачастую затруднительно в связи с их высокой стоимостью и довольно сложным для ручной пайки корпусом BGA(Ball Grid Array).
Микроконтроллер STM32F405V/407V стоит недорого и имеет стандартный корпус QFP (Quad Flat Package) 64/100 с шагом выводов 0,5 мм, что позволяет работать с ним в домашних условиях. Он содержит богатый набор периферийных модулей, необходимых для управления синтезаторами или аттенюаторами. Тактовая частота ядра — 168 МГц, чего вполне достаточно для несложных задач цифровой обработки сигналов.
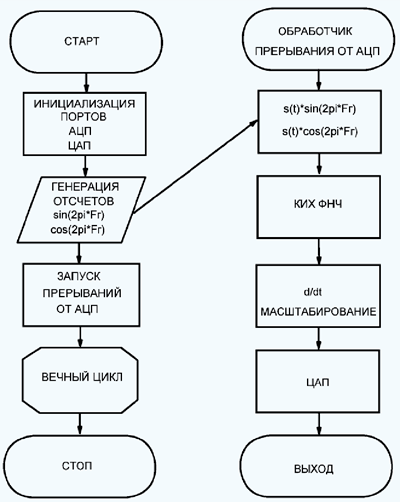
Рассмотрим основные алгоритмы цифровой демодуляции АМ/ЧМ-сигналов после переноса их на низкую промежуточную частоту (порядка 100 кГц). Общая блок-схема цифрового демодулятора ЧМ-сигнала приведена в статье «Демодуляция сигналов с угловой модуляцией. PM и FM демодуляторы». — URL: http://www.dsplib.ru/content/ fmdemod/fmdemod.html (27.08.2018). При этом для демодуляции АМ-сигналов выходные данные необходимо снимать с блока вычисления суммы квадратов сигналов, взяв от неё квадратный корень. Таким образом, наиболее сложный вариант с точки зрения процессорного времени обработки представляет демодулятор ЧМ-сигнала.
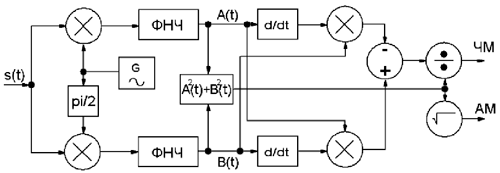
Рис. 1. Блок-схема квадратурного АМ/ЧМ демодулятора
Блок-схема квадратурного АМ/ЧМ демодулятора приведена на рис. 1. Стандартный подход для «обкатки» алгоритмов ЦОС (цифровой обработки сигналов) в микроконтроллерах или ПЛИС заключается в предварительном тестировании и оптимизации алгоритма в средах математического проектирования, таких как SCILAB, OCTAVE, MATLAB. Таким же образом поступим и мы.
Ниже приведены графики для ЧМ-сигнала со следующими параметрами:
— частота несущей 150 кГц;
— девиация частоты 50 кГц;
— частота однотонального модулирующего сигнала 15 кГц.
Параметры этого сигнала соответствуют параметрам сигнала ЧМ-радиовещания.
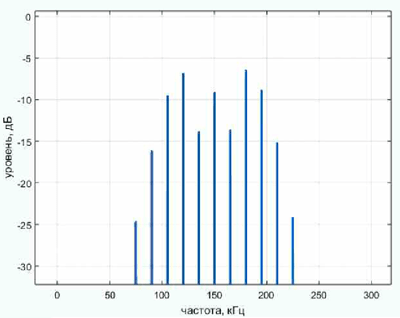
Спектр ЧМ-сигнала s(t) на входе демодулятора показан на рис. 2. Полоса занимаемых им частот от 85 до 215 кГц. Таким образом, по теореме Котельникова частота дискретизации АЦП должна быть не меньше 600 кГц. В проекте частота дискретизации выбрана равной 665 кГц.
Рис. 2. Спектр ЧМ-сигнала s(t) на входе демодулятора
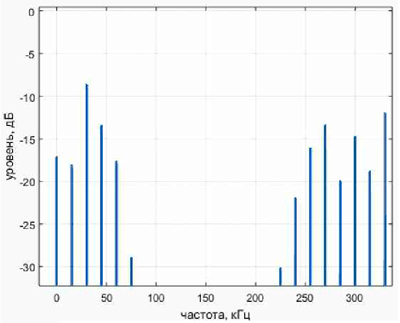
Для расчёта ФНЧ рассмотрим спектр сигнала после квадратурных смесителей, изображённый на рис. 3. Видно, что частота среза ФНЧ должна быть 100 кГц, чтобы отфильтровать зеркальные побочные сигнала. Фильтр был спроектирован в программе WinFilter. — URL:http://www.winfilter.20m.com (27.08.2018). Он имеет следующие параметры: частота среза — 100 кГц, затухание на частоте 200 кГц — 60 дБ, частота дискретизации — 665 кГц, тип фильтра — КИХ (с конечной импульсной характеристикой), порядок —11.
Рис. 3. Спектр сигнала после квадратурных смесителей
Фильтры БИХ (с бесконечной импульсной характеристикой) при аналогичных параметрах могут иметь меньший порядок, но их фазочастотная характеристика нелинейна, что приводит к сильным искажениям сигнала, в связи с этим применяется фильтр КИХ.
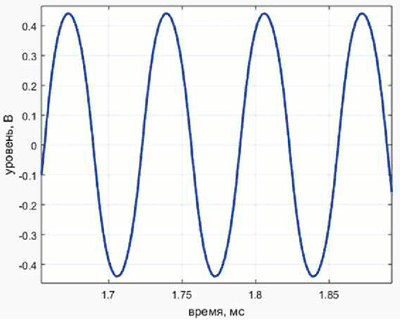
Сигнал на выходе модели демодулятора показан на рис. 4. Видно, что его искажения незначительны. Таким образом, параметры рассчитанных ФНЧ корректны.
Рис. 4. Сигнал на выходе модели демодулятора
Рассмотрим реализацию алгоритма ЧМ-демодулятора в микроконтроллере STM32F407V. Этот микроконтроллер имеет тактовую частоту 168 МГц, при этом она может быть увеличена до 216 МГц (работает, но полных испытаний не проводилось). Большинство инструкций выполняются за один такт. Из интересующей нас периферии он имеет три блока АЦП с разрешением в 12 бит, частотой дискретизации до 2,4 МГц и опорным напряжением 2,5 В, два модуля ЦАП с частотой до 1 МГц.
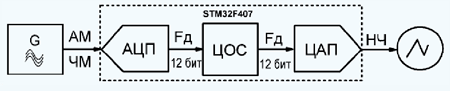
Блок-схема аппаратной части демодулятора на микроконтроллере приведена на рис. 5. ЧМ-сигнал s(t) подавался от функционального генератора DG4162.
Рис. 5. Блок-схема аппаратной части демодулятора на микроконтроллере
Блок-схема алгоритма программы микроконтроллера изображена на рис. 6. Основной код программы выполняется в обработчике прерывания по готовности АЦП. Следовательно, основной цикл программы можно использовать для управления и настройки приёмника. Время, затрачиваемое на цифровую обработку при тактовой частоте ядра 216 МГц, — 900 нс. Таким образом, загрузка процессора не превышает 60 % при частоте дискретизации 665 кГц.
Рис. 6. Блок-схема алгоритма программы микроконтроллера
Для разработки программы использовалась среда CoIDE, а для инициализации периферии применялись модули, сгенерированные в программе CUBE MX С-компилятора — GCC. Все данные представлены в целочисленных переменных.
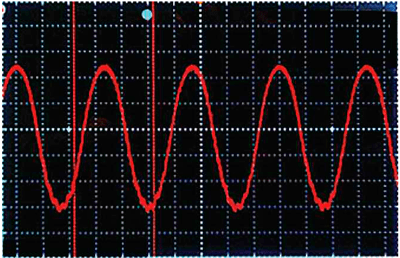
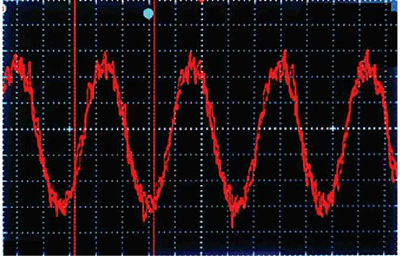
На рис. 7 показана осциллограмма демодулированного сигнала на выходе ЦАП при размахе несущей 2,5 В или 0 дБ (полный динамический диапазон АЦП, определяемый опорным напряжением 2,5 В). При этом за счёт операции масштабирования для устранения амплитудной модуляции работоспособность алгоритма сохраняется вплоть до размаха несущей 50 мВ или -30 дБ. Сигнал на выходе ЦАП при таком уровне входного сигнала показан на рис. 8.
Рис. 7. Осциллограмма демодулированного сигнала на выходе ЦАП
Рис. 8. Сигнал на выходе ЦАП
Полученные результаты позволяют рекомендовать для использования в качестве АМ/ЧМ демодулятора высокопроизводительные микроконтроллеры в «дружелюбном» корпусе и небольшой стоимостью. Такое применение весьма актуально для построения автономных трансиверов. При этом описанный алгоритм можно применять как для демодуляции широкополосного ЧМ-сигнала (Wide Band FM), так и для узкополосного (Narrow Band FM). Отличие будет заключаться только в параметрах ФНЧ. Для создания полноценного прототипа необходимо использовать не табличный вариант вычисления отсчётов гетеродина, а алгоритм CORDIC (Coordinate Rotation Digital Computer), чтобы избежать артефактов в сигнале на стыках фрагментов синусоиды. Также необходимо добавить цифровую петлю ФАПЧ (фазовой автоподстройки частоты) для устранения дрейфа аналогового гетеродина.
Материалы проекта имеются здесь.
Автор: М. Дахин, г. Воронеж.
Java — язык программирования общего назначения. Общего назначения — значит можно писать почти любые программы. Вот я и попытался написать программу, которую обычно пишут на С или C++. Под катом я попытаюсь рассказать, как я декодировал спутниковые снимки с Метеор-М №2.
Предисловие
Когда я впервые заинтересовался декодированием спутниковых сигналов, то был, прямо говоря, удивлён. Сейчас софт для декодирования сигналов выглядит так же, как и библиотеки общего назначения лет 20 назад. Каждый пишет, что хочет, в каком хочет формате и совершенно не заботится о результатах. Яркий тому пример — декодирование сигнала с Метеор-М. Обычно алгоритм получения картинки выглядит следующим образом:
- Записать сигнал
- Запустить SDR# с определёнными плагинами и настройками и демодулировать сигнал. На выходе получается бинарный файл.
- Запустить LRPToffLineDecoder и на вход передать бинарный файл, полученный ранее.
- Из LRPToffLineDecoder сохранить картинку куда-нибудь.
Видимо, всех радиолюбителей такой подход устраивал, если за 9 лет существования спутника на орбите, ничего лучше не было придумано. Но для автоматического получения картинки такой подход не работает:
- Весь софт работает под Windows
- Нельзя запускать в headless режиме. Софт — это формочки с кнопочками.
- Невозможно получить обратную связь по приёму сигнала. Нет никаких метрик, по которым можно было бы оценить хорошо или плохо была принята картинка.
Из-за этого я забросил вэб формочки кровавого энтепрайза и начал долгое погружение в гремучий мир DSP. На полное декодирование сигнала у меня ушло 2 месяца свободного времени.
Разбор сигнала логически можно представить как две фазы:
- Демодуляция. Преобразование аудио-сигнала в информацию.
- Декодирование. Преобразование информации в понятный пользователю вид.
Демодуляция
Согласно официальной документации сигнал модулирован с помощью QPSK. Если вкратце, то для передачи двух бит информации используется одно положение фазы.
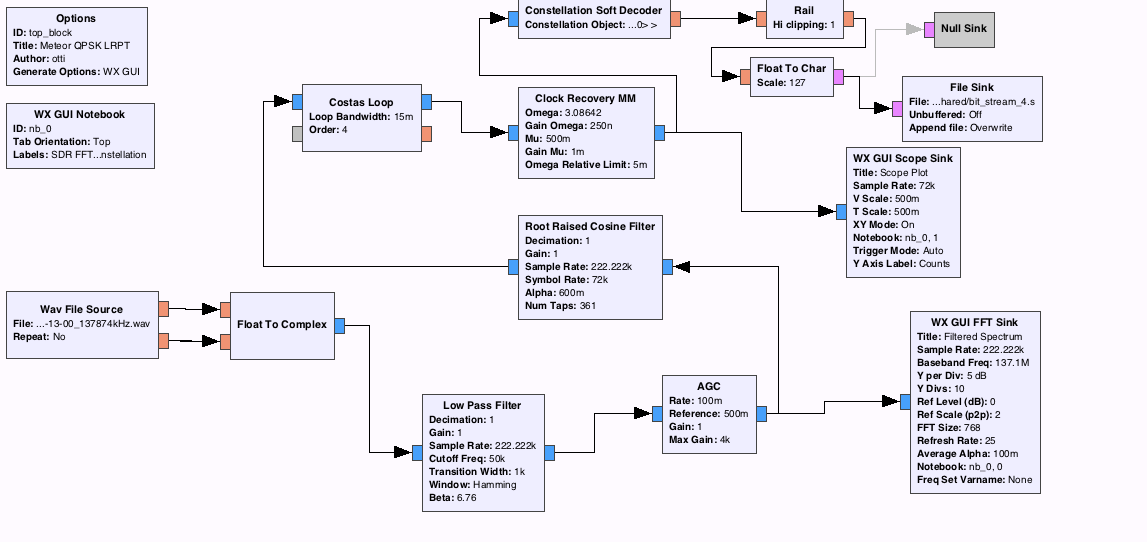
Итак, нужно демодулировать QPSK сигнал на Java. То ли никому это неинтересно, то ли Java медленная, но я не нашёл ни одной библиотеки, которые бы это делали. Поэтому я взял существующий проект демодуляции QPSK сигнала для GNURadio и начал переписывать блоки на Java.
Блоки демодуляции
WavFile source и Float to Complex. Чтение из .wav файла IQ сигнала. Значения записаны в файле последовательно. Сначала реальная часть, потом мнимая, потом реальная и так далее. В GNURadio есть свои типы данных и каждый блок рассчитан для работы только с определёнными. Так как у нас QPSK модуляция, то нам нужно использовать комплексные числа. Здесь ничего сложного, так как в Java есть поддержка .wav файлов — AudioSystem.getAudioInputStream(inputStream).
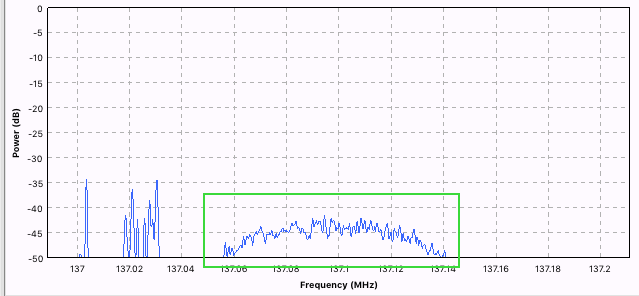
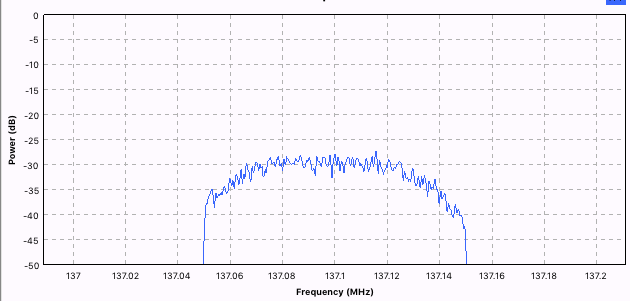
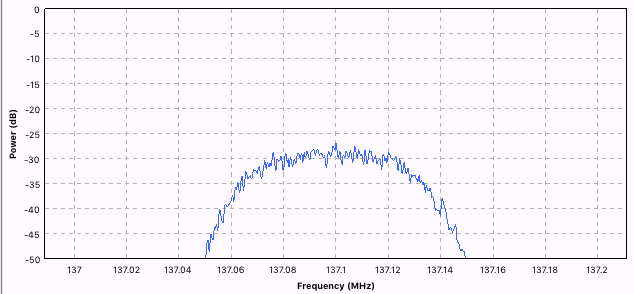
Low Pass Filter. Это первый фильтр, который предназначен для фильтрации низких частот. Так как наш сигнал занимает 130Mhz, то нам надо отфильтровать лишние частоты.
На картинке выше, частоты нашего сигнала обведены зелёным. Остальные частоты справа должны быть отфильтрованы. Это делается с помощью КИХ-фильтра. Для программиста это выглядит как:
- Взять последние N значений, текущее и положить в массив
- Перемножить получившийся массив с заранее заданным (вычисляется из ЛАФЧХ фильтра). По сути, перемножение одного вектора на другой.
- Все значения результирующего массива сложить.
- Это и будет результат.
AGC. Автоматическая регулировка усиления.
С точки зрения реализации — перемножение входного сигнала на некий уровень и вычисление следующего уровня в зависимости от текущего.
Root Raised Cosine Filter. Используется для уменьшения Intersymbol interference. Если вкратце, то при получении сигнала одни уровни переданного сигнала могут накладываться на последующие. Чтобы выделить максимальный уровень сигнала между символами, применяют этот фильтр. Работает так же как и Low Pass Filter, но использует другую ЛАФЧХ
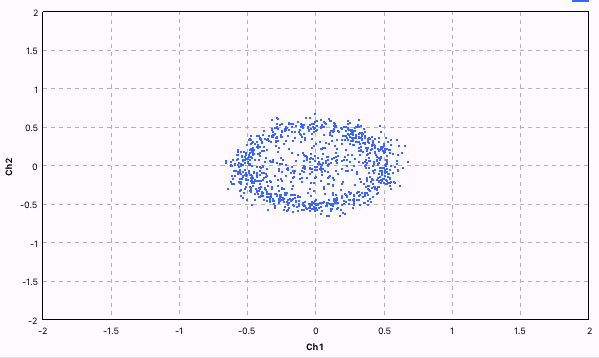
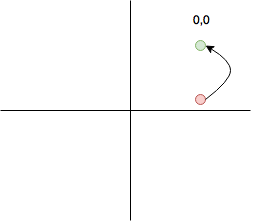
Costas Loop — это алгоритм фазовой подстройки частоты. Для чего он нужен? Например, для того, чтобы корректировать доплеровское смещение частоты. Так как, мы точно знаем, что фаза у нас скачет по четырём уровням, то можно сравнивать значение двух разных фаз. Если оно отличается на дельту, то корректировать частоту. Это ярче всего видно на картинках внизу.
До коррекции частоты, у нас круг (почти). Это значит, что частота немного меняется каждый раз, и точки фазы не попадают в одно и то же место.
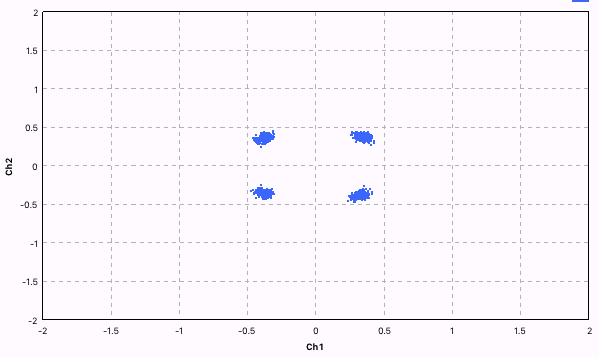
Здесь уже значительно лучше — видны 4 отчётливые точки фазы.
Clock recovery MM. Этот блок пытается восстановить шаг часов передатчика и отбрасывает все сэмплы, которые не относятся к изменению уровня. Примерная схема работы изображена ниже:
После того как все лишние сэмплы выкинуты, получается хорошее QPSK созвездие.
Constellation Soft Decoder. Этот блок преобразует координаты в вероятность битов. Тут надо остановиться поподробнее, так это очень важно в дальнейшем. Допустим все точки у которых координаты положительные будут отображаться в пару “00”.
Теперь допустим, что мы получили значение в красной точке.
Если мы будем делать жёсткое решение, то координаты красной точки мы преобразуем в пару “00”. При этом мы потеряем информацию о том, что точка-то почти “01” (в нижним квадранте). А эта информация на самом деле может помочь в декодировании. Есть алгоритмы, которые дают лучшие результаты, если передать эту информацию. Поэтому вместо того, чтобы принимать жёсткое решение, надо посчитать вероятность 0 и вероятность 1. Например, 100% вероятность нахождения в правом верхнем квадранте будет 255,255. Использование мягких решений увеличивает поток данных в 8 раз, зато даёт более лучшие результаты при декодировании сигнала. Для того чтобы посчитать мягкое решение, необходимо рассчитать расстояние между текущей точкой и каждой из точек созвездия.
Rail, Float to char, File sink. Эти блоки немного преобразуют результаты и записывают их в файл. Для моего декодера записывать результаты в промежуточный файл не надо. Но в целях отладки было крайне полезно сначала демодулировать сигнал из Java, а затем посмотреть может ли LRPToffLineDecoder извлечь картинку.
Декодирование
Итак, у нас есть поток 0 и 1 из которого нужно получить картинку. Для начала необходимо открыть официальную документацию, где неплохо описана структура пакетов. Некоторые моменты там были опущены, поэтому я открыл еще более официальную документацию.
Декодирование состоит из следующих этапов:
- поиск в потоке бит синхромаркера. Каждый пакет начинается с него.
- после того как синхромаркер был найден, декодировать следующие 16384 бита алгоритмом Витерби
- результат подвергнуть скрэмблированию, после чего
- применить коды Рида Соломона и извлечь данные транспортного кадра
- из последовательности транспортных кадров извлечь последовательность парциальных пакетов. Для тех, кто изучал модель OSI вопросов быть не должно.
- из парциальных пакетов извлечь MCU формата JPEG
- декодировать пикселы JPEG, используя коды Хаффмана и Run-length coding
- правильно заполнить пикселами картинку с учётом пропущенных пакетов
- наложить 3 канала друг на друга с учётом пропущенных пакетов
Пожалуй я не буду здесь рассказывать про каждый из алгоритмов. Они сами по себе потянут на отдельную статью. Хочу лишь выложить результаты работы моей программы, официальной и на паскале.
К сожалению общая картина занимает 4500x2800px, поэтому я привожу сильно пожатую версию.
Оптимизации
А при чём тут Java? — скажут самые стойкие, кто смог дочитать до сюда.
Сейчас будет немного Java. Дело в том, что оптимизацию имеет смысл для корректно работающей программы. После каждого шага оптимизации можно запустить тесты и убедиться, что всё по-прежнему работает корректно.
Итак, я начну с декодирования. При запуске профайлера, ничего странного не обнаружилось:
- одно ядро работает на полную мощность
- самый горячий метод — это декодирование Витерби. Сложность этого алгоритма О(T*S), где T — это длина массива данных, S — пространство состояний. В нашем случае у нас 8 (бит) * 4 (00,01,10,11) = 32.
Помимо CPU, я запустил еще анализ аллокаций объектов. Оказывается, этот метод создаёт миллионы короткоживущих объектов. Они создают лишнюю нагрузку на GC и процессор. Посмотрим, можно ли это оптимизировать. Наивная реализация создаёт связный список для хранения решений каждого входящего бита:
LinkedList<long[]> decisions = new LinkedList<long[]>();
for (int i = 0; i < data.length; i += 2) {
long[] d = new long[2]; //decision
for (int b = 0; b < 32; b++) {
d[b / 16] = ...;
}
...
decisions.add(d);
}
Это можно попробовать развернуть в одномерный массив и обращаться к результатам хитро вычисляя индекс. Например, так:
long[] decisions = new long[data.length];
for (int i = 0; i < data.length; i += 2) {
decisions[i + b / 16] = ...;
}
В итоге на одно декодирование создаётся один объект — массив decisions. ViterbiSoft можно ещё дальше оптимизировать. Например, зная то, что размер массива всегда одинаковый, создать long[] decisions в конструкторе и переиспользовать.
Ещё одним проблемным местом оказался класс FixedLengthTagger. Этот класс содержит скользящее окно. Оно работает следующим образом:
- новый байт читается из источника
- записывается в конец окна
- если размер окна больше размера пакета, то удалить байт из начала окна
Наивная реализация использовала LinkedList и алгоритм движения окна был такой:
window.offerLast(curByte);
if (window.size() > packet_len) {
window.removeFirst();
}
На самом деле это очень накладная операция, так как на каждую операцию offerLast внутри LinkedList создаётся объект Node. Он будет содержать наш байт и иметь ссылки на следующий элемент списка и предыдущий. Однако, зная, что размер нашего окна фиксированный, его можно заменить на циклический массив:
window[windowIndex] = curByte;
windowIndex++;
if (windowIndex >= window.length) {
windowIndex = 0;
}
Для того чтобы правильно взять его содержимое надо скопировать данные до текущего указателя первыми и после текущего указателя последними. Как то так:
byte[] packet;
System.arraycopy(window, windowIndex, packet, 0, window.length - windowIndex);
System.arraycopy(window, 0, packet, window.length - windowIndex, windowIndex);
Эти две оптимизации позволили уменьшить время декодирования файла с 4 минут до 20 секунд. Для сравнения LRPToffLineDecoder делает это за 40 секунд.
Декодирование можно ещё немного оптимизировать, но в ущерб читаемости. Вместо этого можно попробовать ускорить демодуляцию.
Алгоритмы демодуляции на входе получают большой поток данных, а на выходе выдают сравнительно небольшой. Поэтому эти алгоритмы очень чувствительны к различным оптимизациям. При запуске профайлера, видно, что большая часть приходится именно на математические операции внутри блоков.
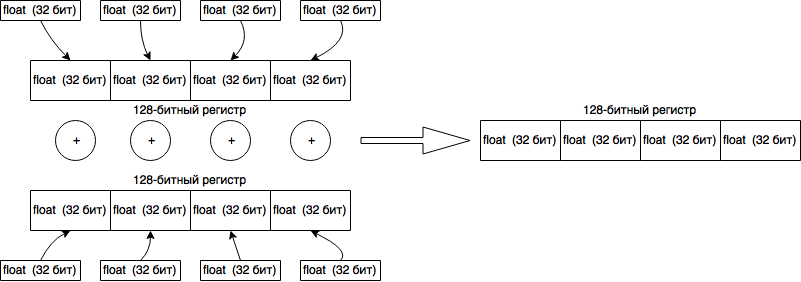
Тут мало что можно сделать: память не выделяется, безумных циклов нет. Единственное, что интересно проверить это компилирует ли Java JIT код в SIMD инструкции. Если вкратце, то это специальные инструкции процессора, которые работают с 128битными регистрами и обрабатывают их одной командой. Схематично это выглядит так:
Как видно, такие инструкции идеально ложатся на КИХ-фильтры. GNURadio использует библиотеку VOLK, которая в зависимости от поддерживаемой архитектуры, может использовать SIMD инструкции. В Java скорей всего вызывать JNI обёртку будет значительно затратнее, чем выигрыш от использования таких инструкций. Одна надежда на JIT, который может оптимизировать перемножение одного массива на другой. Чтобы это проверить, необходимо запустить JVM с опцией “-XX:CompileCommand=print,*FIRFilter.filterComplex”. Она заставит JVM выводить ассемблерный код для метода filterComplex из класса FIRFilter.
Вот что у меня получилось при запуске с Oracle JDK 1.8.0_161 на MacBook Air:
0x0000000115994750: vmovss 0x10(%r10,%r11,4),%xmm1
0x0000000115994757: vmulss 0x10(%rcx,%r11,4),%xmm1,%xmm4
0x000000011599475e: vmulss 0x10(%r8,%r11,4),%xmm1,%xmm1
0x0000000115994765: vaddss %xmm2,%xmm4,%xmm3
0x0000000115994769: vaddss %xmm0,%xmm1,%xmm0
0x000000011599476d: movslq %r11d,%r9
0x0000000115994770: vmovss 0x1c(%r10,%r9,4),%xmm2
0x0000000115994777: vmulss 0x1c(%rcx,%r9,4),%xmm2,%xmm8
0x000000011599477e: vmulss 0x1c(%r8,%r9,4),%xmm2,%xmm1
0x0000000115994785: vmovss 0x14(%r10,%r9,4),%xmm4
0x000000011599478c: vmulss 0x14(%rcx,%r9,4),%xmm4,%xmm2
0x0000000115994793: vmulss 0x14(%r8,%r9,4),%xmm4,%xmm5
0x000000011599479a: vmovss 0x18(%r10,%r9,4),%xmm4 ;*faload
; — ru.r2cloud.jradio.blocks.FIRFilter::filterComplex@24 (line 26)
Судя по всему SIMD инструкции не используются.
Ещё одним интересным местом стало вычисление sincos. Блок Costasloop вычисляет значение синуса и косинуса для одного и того же угла (фазы) для каждого входящего значения. В CPU есть специальная команда — fsincos. Она вычисляет одновременно синус и косинус угла. Однако, в Java такой функции нет. Да и реализовывать её непонятно как: надо либо возвращать double[] (а это сильно ударит по GC), либо возвращать одно значение как результат работы функции, а другое через изменяемый параметр (double в функцию Java передаётся копированием, а Double опять же ударит по GC). Наивная же реализация выглядит так:
float sinImg = (float) Math.sin(-d_phase);
float cosReal = (float) Math.cos(-d_phase);
Можно попробовать вспомнить тригонометрию и заменить на:
float sinImg = (float) Math.sin(-d_phase);
float cosReal = (float) Math.sqrt(1 - sinImg * sinImg) + calculate sign;
Переход с Math.cos на Math.sqrt позволил сократить время демодуляции с 6 минут до 5 минут и 30 секунд. Тригонометрические операции можно ещё больше ускорить, если использовать таблицы поиска. Однако, я пока не готов исследовать зависимость результатов декодирования от точности таблиц. Может быть кто-нибудь поможет с этим?
Заключение
Поскольку я использовал одни и те же блоки для демодуляции сигнала, то можно сравнить время работы Java программы и GNURadio. Как и ожидалось, GNURadio быстрее: ~2 минуты против 5.5 минут. Да, Java почти в 2 раза медленнее. Но, если учесть, что файл записывался в течение 15 минут, то производительности Java вполне хватит, чтобы в реальном времени демодулировать сигнал.
Исходные данные:
1. Файл оцифрованных сигналов с выхода приемника в широкой полосе частот. Например у вас есть АЦП с частотой дискретизации равной 200 МГц. С помощью такого АЦП вы можете оцифровать сигналы в полосе до 100 МГц. Затем в отложенном режиме проанализировать и демодулировать все сигналы находящиеся в этом файле.
2. Параметры сигнала полученные в результате предварительного анализа:
- частота дискретизации АЦП
- разрядность АЦП
- несущая частота
- тактовая частота
- вид модуляции
Структурная схема квадратурного демодулятора
Частота дискретизации сигнала в АЦП не кратна тактовой частоте сигнала и в оцифрованном файле может быть больше чем один сигнал (до 300). По этим причинам структурная схема демодулятора имеет вид, приведенный на рис. 1.

Назначение, состав, принцип работы составных модулей
1. Модуль чтения из файла. Здесь все просто. Например в файле хранятся 16-ти битные отсчеты АЦП. Демодулятор работает с числами двойной точности (double). Модуль предназначен для чтения отсчетов АЦП из файла и преобразование их в double формат. Следует заметить, что есть тут одна тонкость. Следующим модулем является FFT фильтр в котором используется быстрое преобразование Фурье для работы которого необходимо, чтобы размер обрабатываемых блоков был кратен степени 2. Например 218 = 262144 отсчетов АЦП.
2. FFT фильтр. Как я уже говорил в файле хранятся сигналы в некоторой полосе частот. Таких сигналов в файле может быть очень много. Для дальнейшей работы с сигналом необходимо его сначала “вырезать“ удалив все ненужные сигналы. Лучше всего для этого подходит фильтрация в частотной области. Если очень по простому то операция фильтрации состоит из 3-х частей:
— Выполняется прямое преобразование Фурье для получение спектра сигнала;
— Обнуление в спектре сигнала лишних частот. Так как мы знаем несущую частоту и ширину спектра сигнала это не представляет трудов;
— Выполняется обратное преобразование Фурье.
В итоге мы получаем отфильтрованный сигнал. Это если по простому, но есть несколько тонкостей. Дело в том, что так как мы имеем дело не с бесконечным сигналом, а с блоками конечной длины, то на краях блока возникают искажения сигнала. Для того чтобы избавиться от искажений, необходимо производить фильтрацию блоков с перекрытием (внахлест). Более детально об этом можете почитать в статье FFT анализ где автор “на пальцах” рассказывает об FFT фильтрации.
3. Формирователь квадратур. Задача этого модуля очень проста как и его реализация — это перенос спектра сигнала на нулевую частоту и формирование квадратурных составляющих I и Q. Надо понимать, что на вход блока подается отфильтрованный сигнал. Математически выглядит все очень сложно. Кому интересно можете прочитать в книге «Цифровая связь» автор Прокис Дж. стр. 287 внизу страницы начиная со слов “Сигнал КАМ и многопозиционный ФМ можно представить так”.
Если своими словами то на передающей стороне спектр сигнала формировался из 2-х квадратурных составляющих I и Q, а наша задача на приемной стороне получить их. Делается это очень просто. Сначала высокочастотный сигнал умножается на несущую с частотой равной несущей сигнала. Что происходит при умножении? Гармонические составляющие двух сигналов складываются, вычитаются и т.д. Нам интересно их вычитание. Если принять, что частоты умножаемых сигналов равны, то при вычитании получается 0. Таким образом мы получаем перенос спектра сигнала в 0. При умножении получается куча других гармонических составляющих которые нам не нужны. Как от них избавиться будет описано ниже. Так мы получили первую квадратурную составляющую. Чтобы получить вторую необходимо тот же высокочастотный сигнал умножить на несущую , но теперь сдвинутую по фазе на 90°.
4. Коммутатор. В статье на рисунке 7 представлена схема частного случая когерентного демодулятора когда частота дискретизации сигнала в АЦП берется кратной тактовой частоте сигнала: fд = 2ifт, где i = 2,3,4,… В моем случае такая схема не подходила потому как тактовая частота сигналов в оцифрованном сигнале может быть разной. В этих случаях используется схема приведенная в той же статье на рисунке 8.
В моем случае эта схема претерпела изменение и пришлось добавлять коммутатор. Дело в том, что разброс тактовых частот сигналов на столько велик, что в некоторых случаях необходимо производить децимацию сигнала в других интерполяцию. В зависимости от значения тактовой частоты выбирается одна из двух цепей обработки.
5. Приведение частоты дискретизации к 10*Ft. На данном этапе обработки сигнала существует 2 проблемы. Первая проблема — это то, что в формирователе квадратур при умножении получается куча паразитных гармонических составляющих. От них можно просто избавиться с помощью фильтра нижних частот (ФНЧ). Вторая проблема — это то, что тактовая частота сигнала не кратна частоте дискретизации. Эта проблема решается с помощью блоков децимации и интерполяции.
Моей задачей было разработать схему которая решает обе задачи сразу так как они тесно связаны друг с другом. Дело в том, что децимация не возможна без низкочастотной фильтрации.
Пару слов про децимацию. Нельзя просто так выбросить (удалить) лишние отсчеты из сигнала.

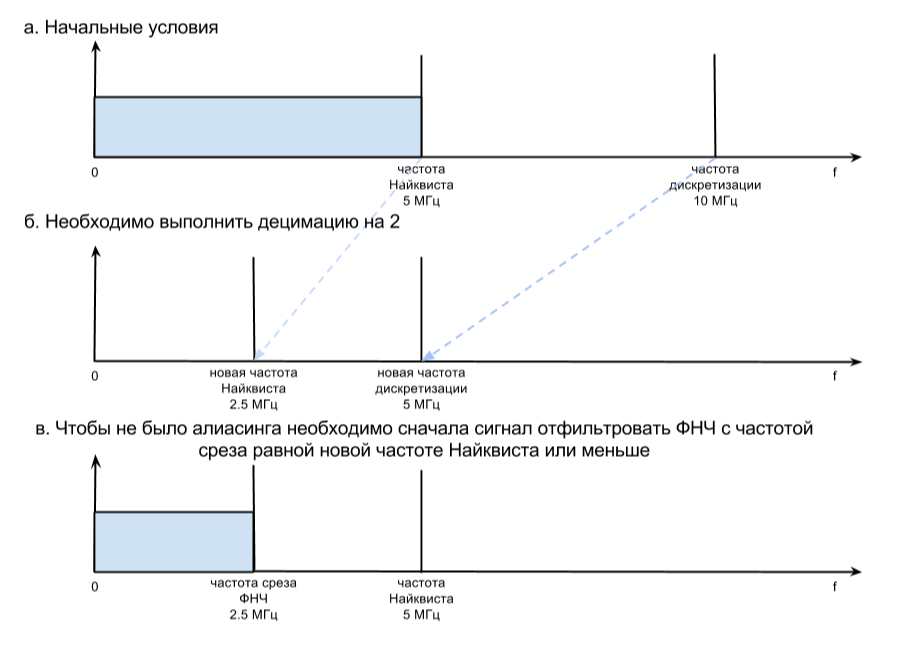
Казалось вроде все просто. Если надо уменьшить частоту дискретизации вдвое, то просто удаляешь отчеты через один. Если втрое, то оставляешь каждый третий отсчет и т.д. Но не тут то было. Для осуществления децимации необходимо выполнить условие, чтобы исходный сигнал не содержал частоты, превышающие частоту Найквиста децимированного сигнала, иначе при децимации будет иметь место алиасинг (наложение спектров).
Например, есть сигнал с частотой дискретизации 10 МГц, тогда частота Найквиста будет равна 5 МГц (Рисунок 3 п. а). Предположим, что нам необходимо произвести децимацию в 2 раза. В этом случае новая частота дискретизации будет равна 10 / 2 = 5 МГц, а новая частота Найквиста будет равна половине новой частоты дискретизации 5 / 2 = 2.5 МГц (Рисунок 3 п. б). Таким образом для того , чтобы не внести искажения в сигнал связанные с алиасингом необходимо перед процедурой прореживания (удаления) произвести низкочастотную фильтрацию фильтром полоса пропускания которого должна быть меньше новой частоты Найквиста (Рисунок 3 п. в).
С фильтрацией побочных гармоник вроде разобрались.
Второй не решенной задачей является то, что частота дискретизации не кратна тактовой частоте и количество отсчетов АЦП на такт величина не постоянная. Если решить эти проблемы то дальнейшая схема демодулятора станет универсальной и не будет зависеть от тактовой частоты сигнала. В результате исследований я пришел к тому, что для дальнейшей обработки сигнала достаточно 10 отсчетов на такт.
Рассмотрим теперь подробней левую часть блока. Мы видим, что применяется 2-х каскада децимации. Сделано это потому, что если тактовая частота сигнала маленькая, то коэффициент децимации становится на столько большим, а частота Найквиста на столько низкой, что трудно реализовать ФНЧ. Например при частоте дискретизации 200 МГц и тактовой частоте сигнала 20 КГц мы имеем 200 МГц / 20 КГц = 10000 отсчетов на такт. Делим полученное число на 10 так как на выходе хотим получить фиксированную частоту дискретизации 10*Ft. Получаем величину 10000 / 10 = 1000. В этом случае нам необходимо произвести децимацию в 1000! раз.
Для решения этой проблемы была разработана схема поэтапной децимации из 2-х каскадов. При таком подходе коэффициенты децимации каскадов умножаются. То есть чтобы реализовать децимацию в 1000 раз достаточно 2-х каскадов с децимацией 25 и 40. В случае если коэффициент децимации не большой то используется только один каскад. Коэффициенты децимации подбираются таким образом чтобы максимально приблизить итоговую частоту дискретизации к 10*Ft.
6. Модули работающие на частоте 10*Ft. Начиная с этого этапа все модули демодулятора работают в одинаковых условиях вне зависимости от начальных условий. Это очень удобно для отладки и позволяет использовать следующие модули для различных решений. По сути до этого были подготовительные этапы. Теперь начинается демодуляция. Такое решение удобно еще и тем, что предыдущие этапы можно отбросить если иметь комплексные отсчёты оцифрованного сигнала с частотой дискретизации равной 10*Ft. То есть можно применить схему демодуляции когда фильтрация сигнала, формирование квадратур и децимация выполняется аппаратно. Такое решение на порядки увеличит скорость демодуляции.
Почему именно 10*Ft? Цифра 10 получена в результате экспериментов. Мне хотелось повысить качество работы фазовращателя и согласованного фильтра, но при этом не очень потерять в скорости обработки.
7. Усилитель. Выполняет операцию умножения отсчетов сигнала на величину полученную с выхода системы автоматической регулировки усиления (САРУ).
8. Фазовращатель. При определении параметров сигнала мы получили ошибку определения несущей частоты и ошибку начальной фазы. Ошибка определения частоты сигнала приводит к тому, что на сигнальном созвездии точки постоянно вращаются. Направление вращения (по часовой или против) зависит от знака ошибки. Допустим мы без ошибки определили частоту сигнала или устранили ошибку, но мы не знаем начальную фазу сигнала. Ошибка определения начальной фазы приводит к тому что сигнальное созвездие будет наклонено на угол равный ошибке определения. Модуль фазовращателя устраняет эти ошибки. Его задача не допустить вращение и наклон сигнального созвездия. Фазовращатель работает постоянно так как несущая частота сигнала может быть величиной не постоянной.
9. Согласованный фильтр. При передаче сигналов всегда идет борьба между скоростью передачи и шириной спектра сигнала. Дело в том что чем выше скорость передачи тем шире спектр сигнала. В системах передачи данных от ширины спектра сигнала зависит стоимость оказываемой услуги. Есть еще одна сторона вопроса. По цифровым каналам связи сигналы передаются прямоугольными импульсами. Прямоугольный импульс имеет бесконечный спектр. Крайний случай передачи данных это когда передаются последовательно «0» и «1» (меандр). Спектр меандра пропорционален функции sinc(x).
Для уменьшения ширины спектра на передающей стороне сигнал фильтруется для удаления высокочастотных составляющих, но в результате фильтрации происходит межсимвольная интерференция. Если знать закон (правило) фильтрации, то на приемной стороне можно произвести обратное преобразование которое позволит устранить пагубное влияние межсимвольной интерференции. Этой задачей и занимается согласованный фильтр.
10. Дециматор на 5. Приводит частоту дисктеризации 10*Ft к 2*Ft. Таким образом коэффициент децимации давен 5.
11. Модули работающие на частоте 2*Ft. Начиная с этого этапа все модули демодулятора работают на скорости 2*Ft (удвоенной тактовой). 2*Ft — это минимальная частота на которой могут работать адаптивный корректор и решающее устройство.
12. Адаптивный корректор. В результате прохождения сигнала через атмосферу или например за счет переотражения сигнала от зданий на него накладываются нелинейные помехи характеристика которых тесно связана с характеристикой канала передачи данных. Целью адаптивного корректора является вычисление характеристики канала передачи данных и устранение его влияния на качество сигнала.
13. Принятие решения. Соль демодулятора. Именно тут принимается решение по принятой точке на сигнальном созвездии. Принятая точка «притягивается» к эталонной по критерию минимального расстояния. По двум точкам на плоскости (принятой и эталонной) вычисляются ошибки для системы автоматической регулировки усиления, системы восстановления несущей и системы восстановления тактовой.
14. Петли обратной связи. Для усилителя (7) система автоматической регулировки усиления (САРУ) вычисляет коэффициент на который необходимо умножить сигнал для того чтобы он полностью помещался с сигнальное созвездие. Для фазовращателя (8) система восстановления несущей (СВН) вычисляет ошибку определения несущей частоты и её начальной фазы. Для блоков децимации (5) система тактовой синхронизации вычисляется ошибку определения тактовой частоты и её начальной фазы.
Вот вроде и все. Получилось даже больше чем планировал. Очень надеюсь, что кому то пригодятся мои знания.
Однажды мне прилетела задача реализовать DMR на ПЛИС. Опустившись на дно интернета, я нашел лишь мануал ETSI и пару примеров по генерации кода – с этого начался мой тернистый путь изучения данной тематики. Недавно наткнулся на мем, и тут нахлынули воспоминания. Решил, дабы сэкономить время людей, которые столкнутся с чем-то подобным, поделиться подробным гайдом таких задач с примерами реализации.
Пока писал вступление, совсем забыл про то, ради чего мы здесь, естественно, ради мемов и крутых инженерных фишек!
FPGA по-русски – программируемые пользователем вентильные матрицы. ПЛИС – программируемые логические интегральные схемы.
Главная разница между ПЛИС и FPGA – это то, что первое по сути класс устройств, а второе – вид устройств.
Для чего они нужны и что с ними делать?
ПЛИС имеют широкий спектр применения: их используют в цифровой обработке сигнала, для передачи данных на высокой скорости, для криптографических операций, для систем защиты информации или в качестве прототипов для будущих СБИС (ASIC).
Алгоритмы под ПЛИС реализуются на языках описания аппаратуры, например на Verilog HDL. Так причем же здесь MATLAB?
MATLAB имеет возможность генерации кода HDL, а что более интересно, прямо из него можно получить готовый проект под Vivado и выполнить его синтез и имплементацию уже там. О том как сотворить это чудо, я хочу поговорить с вами далее в статье.
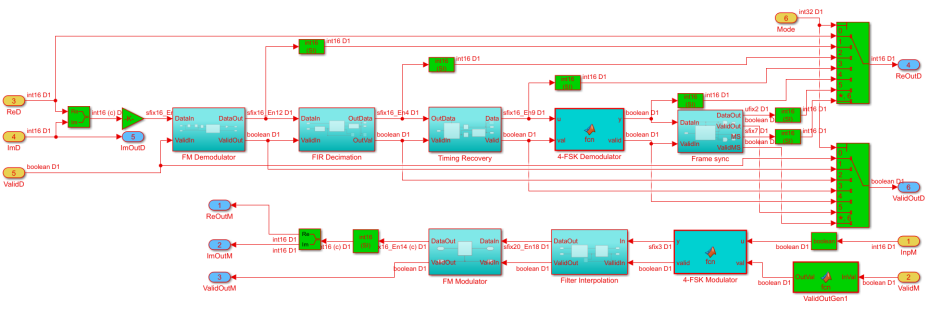
Я расписал подробный гайд, чтобы упростить работу инженеров, проектирующих на ПЛИС. Цель статьи – описание процесса разработки приемопередатчика на ПЛИС по стандарту цифровой подвижной радиосвязи (DMR). Проект будет реализован под отладочную плату ZedBoard Zynq-7000. Для реализации проекта используется подход модельно-ориентированного проектирования (МОП). Его структура отображена на рисунке 1, все достаточно просто: есть приемные и передающие тракты цифровой обработки, которые в итоге мы реализуем на ПЛИС.
Эту задачу можно образно разделить на три этапа:
-
Первый этап – это разработка системной модели. Он позволяет реализовать модель, на основе которой в дальнейшем можно выполнить верификацию разрабатываемых алгоритмов на отладочных или макетных платах за счет взаимодействия с реальным оборудованием.
-
Второй этап – это трансформация модели под генерацию HDL кода. Основными задачами этапа являются перевод всех применяемых в проекте типов данных в фиксированную точку и изменение алгоритмов, не поддерживающих генерацию кода HDL.
-
Третий этап – реализация полученного HDL кода на ПЛИС. Здесь выполняется работа со сгенерированным кодом и Vivado. Главная задача – успешные синтез, имплементация проекта и взаимодействие с полученными файлами прошивки и управляющих программ.
Системная модель
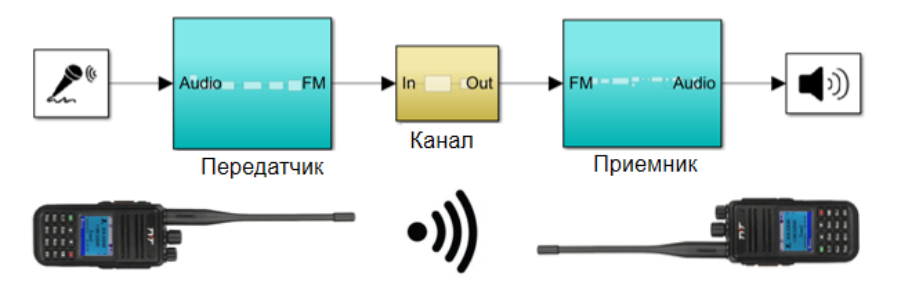
На рисунке 2 представлена системная модель приемопередатчика DMR. Эта модель реализована при помощи Communications System Toolbox, работает в «реальном времени» и позволяет захватывать сигнал с рации и передавать записанные данные на рацию. Также она реализует виртуальную рацию. Для передачи радиосигнала используется ADALM-PlutoSDR. Это отладочная плата на основе трансивера AD9363 и FPGA Xilinx® Zynq Z-7010.
На данном этапе разработки мы получаем возможность отладки приемопередатчика, учитывая факт использования стандартных библиотечных блоков. Мы можем в максимально короткие сроки произвести верификацию разработанных алгоритмов.
В этой статье я не хочу затрагивать анализ системной модели и тратить ваше и свое время на разбор каждого конкретного блока и обзор его функционала. Если кому-то интересен этот вопрос, напишите об этом – я сделаю обзорную статью по каждому блоку и разберу аспекты перевода модели из системной в модель под генерацию HDL кода в деталях.
Единственные блоки, которые я затрону более подробно, это «ADALM-Pluto Radio Transmitter», который позволяет использовать Pluto как передатчик сигнала в эфир, и «ADALM-Pluto Radio Receiver», который в свою очередь принимает сигнал. В данной модели многие алгоритмы написаны MATLAB скриптами, поэтому я думаю, что в дальнейшем найдутся люди, которым будет интересно узнать, как на практике реализуется кадровая синхронизация, перемежители или как формируются заголовки пакетов. Честно говоря, я сам надеюсь на продолжение нашего с вами общения на эту тему.
¯_(ツ)_/¯
На рисунках 3 и 4 я показал работу системной модели и взаимодействие с рацией и Pluto. В этой реализации на приемной и передающей стороне есть задержка, равная длине накапливаемого буфера. На 3 рисунке показана работа передатчика. Как вы видите, рация улавливает сигнал и декодирует адресата, а на рисунке 4 показана работа приемника. На графике MS видны пики корреляции, также можно заметить, что сигнальные конструкции определяются в тот момент, когда я начинаю передачу сигнала с рации, а на графике Error показан сдвиг символьной синхронизации.
Модель для генерации HDL кода. Реализация на ПЛИС.
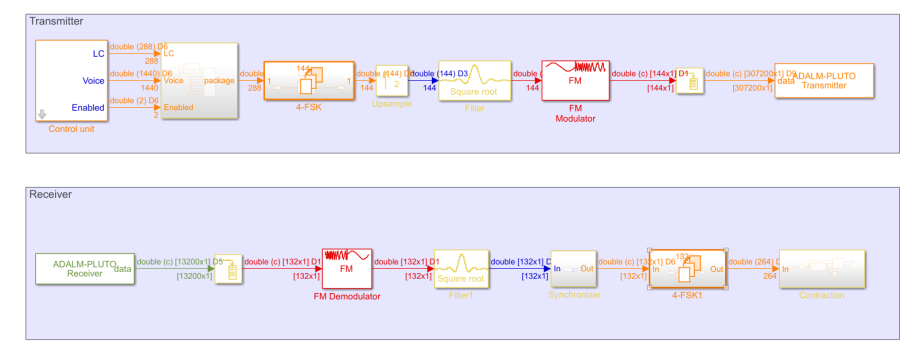
Перейдем к HDL реализации. Что это и зачем оно нужно, мы уже разобрали, предлагаю взглянуть на рисунок 5: на нем представлена HDL модель, построенная на основе системной модели. Отличием от системной модели является использование блоков, поддерживающих генерацию HDL кода, и перевод всего тракта цифровой обработки в фиксированную точку. Для удобства отладки на плате для приемной части реализована возможность переключения режимов, за счет чего у нас есть возможность отследить все изменения данных в процессе обработки. Для передатчика этот подход не использовался, так как он имеет достаточно простую реализацию, и с ним изначально не возникало вопросов.
В этой части я хочу акцентировать внимание на процессе генерации HDL кода из модели, а не на самой модели и ее архитектурных изысках. Первым этапом является подключения САПР Vivado от Xilinx к MATLAB, ниже показан MATLAB скрипт для подключения.
Чтобы сгенерировать код, наверное нам надо задать какие-то настройки, условия под наш проект, но это не точно.)
Дак о каких настройках я говорю и где они находятся?
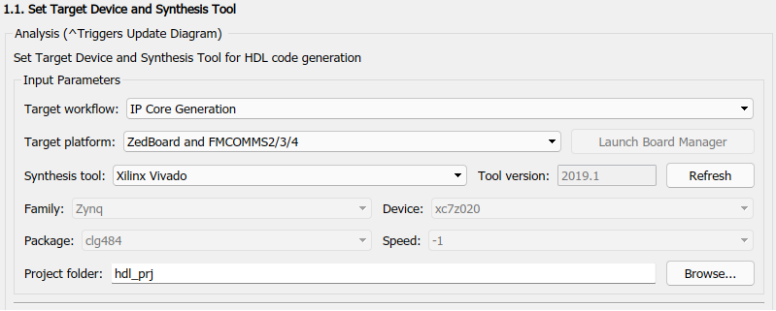
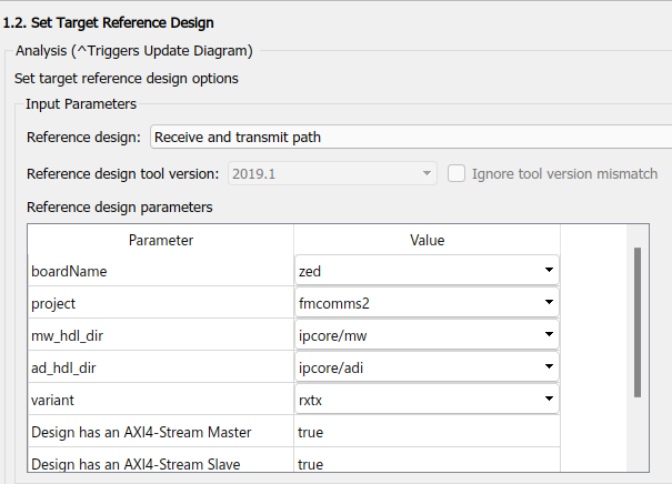
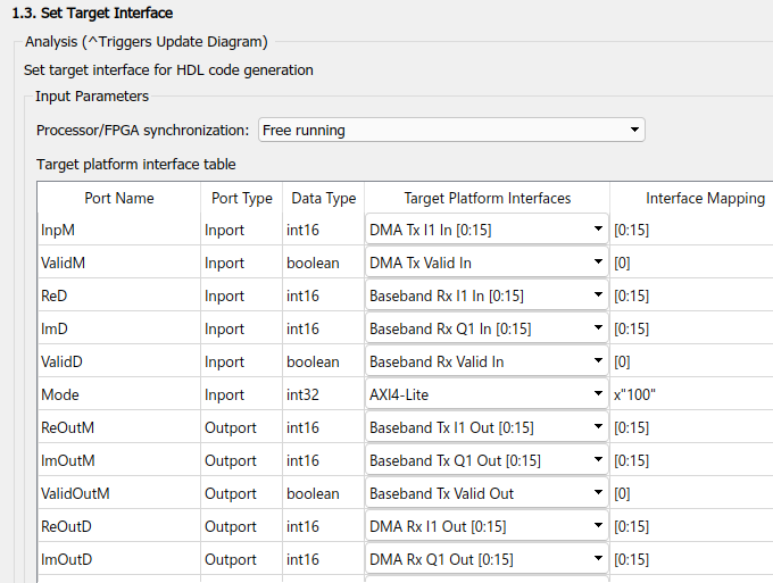
Откроем HDL Workflow Adviser. Там мы увидим эти настройки, на рисунках 7, 9-11 они также показаны и объяснены. На рисунке 7 настройки референса-проекта, здесь мы выбираем плату, под которую будем генерировать код, в нашем случае это ZedBoard + FMCOMMS, сама плата показана на рисунке 8.
На рисунке 9 показаны настройки ядра прошивки, в данном случае мы создаем ядро приемника и передатчика.
На рисунке 11 представлены настройки входных и выходных портов IP-ядра, а также размерности этих портов и их размерности в битах.
После того как мы настроили параметры генерации кода, переходим в пункт 4.1 и создаем проект Vivado с нашим IP-ядром, после чего уже в самой Vivado создаем бинарный файл прошивки (вкладка «Generate Bitstream»). На самом деле не думаю, что на данном этапе хоть у кого-то с первого раза выполнилась имплементация, обычно это всегда несколько дней работы, прежде чем у вас нормально сойдутся тайминги, так что не судите строго за отсутствие описания этой боли в статье. Если интересно, то могу с вами обсудить это в комментариях.)))))
После создание бинарного файла мы получаем полноценную прошивку под ПЛИС, которая выполняет заложенный нами функционал. Залить прошивку на ПЛИС можно несколькими способами: либо использовать загрузчик Vivado (на рисунке 12 показан процесс открытия таргета), либо можно вручную заменить стандартный файл system.bit на сгенерированный system_top.bit, естественно переименовав его в system.bit.
После загрузки прошивки необходимо загрузить управляющую программу. Чувствую назревший вопрос: откуда взялась управляющая программа и почему мы раньше о ней не говорили?
Погодите-погодите, я сам только что о ней вспомнил. Управляющая программа позволяет реализовывать управление интерфейсами на отладочной плате.
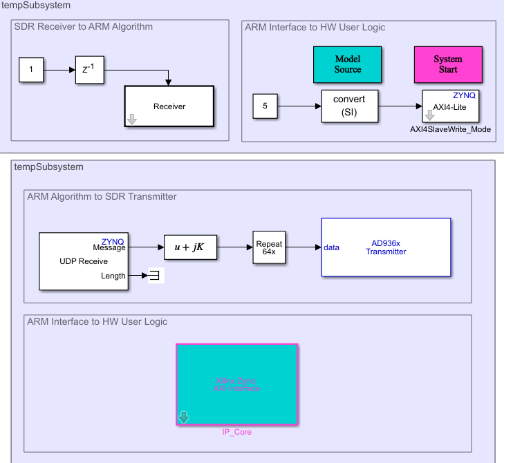
В модели управляющей программы мы объявляем AXI-порт как управляющий. За счет него мы переключаем различные режимы работы приемника, также мы определяем, что по протоколу UDP выполняется прием и передача данных на ПК, компьютер я использую в этой связке для трансляции аудиосигнала от микрофона и к акустическому динамику. И здесь же описана взаимосвязь кристалла ПЛИС с FMCOMMS (блоки AD936x). Сама модель, о которой я так много сейчас сказал, показана на рисунке 13.
Из этой модели при помощи комбинации клавиш Ctrl+B (люблю горячие клавиши, не могу) мы генерируем управляющую программу на языке C и файл *.elf , который дальше можно либо заранее загрузить на SD-карточку отладочной платы и вызывать из командной строки, либо каждый раз загружать ее через командную строку. Для второго варианта используется набор команд, показанный на рисунке 14, первая команда отправляет наш файл по IP платы в корень файловой системы, а дальше уже из-под отладки мы его запускаем.
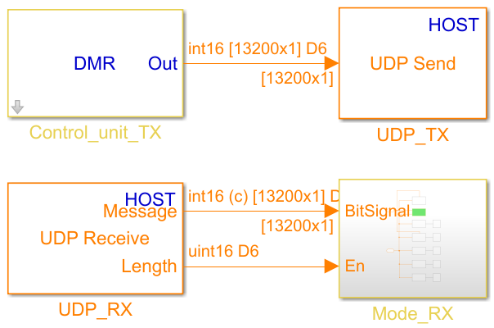
После вызова управляющей программы мы получаем возможность уже с ПК захватывать и передавать данные. На рисунке 15 показана модель, которую я для этого использовал.
Подведем итоги: на мой взгляд я довольно подробно раскрыл методологию МОП, применяемую нами в проектах. Надеюсь, статья была вам интересна и полезна, жду ваших вопросов, критики, буду рад любому фидбеку.))))